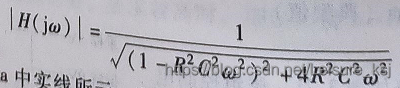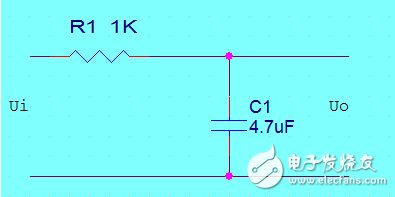
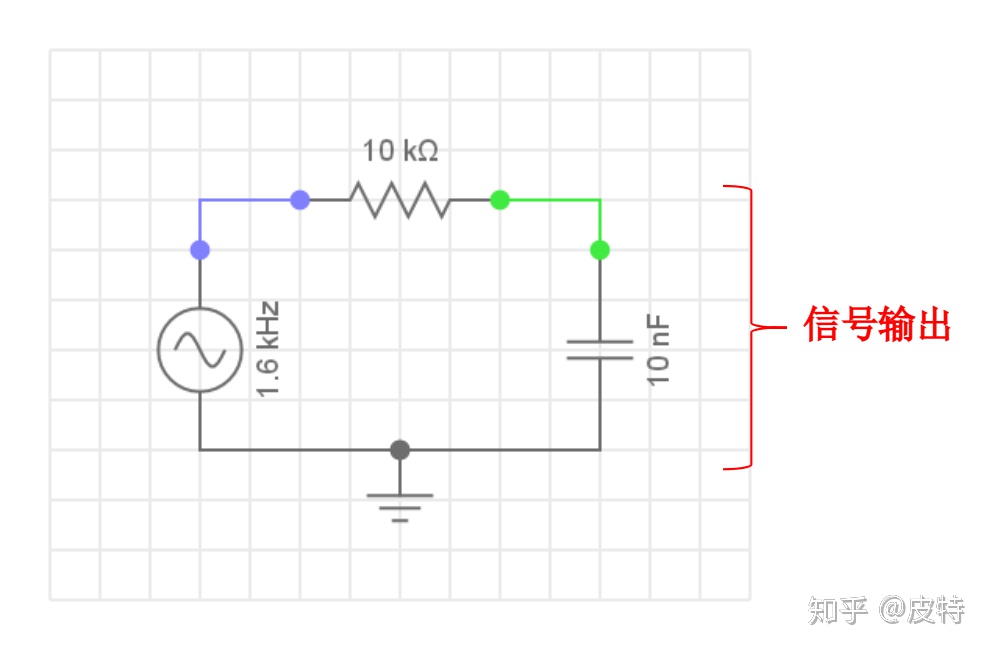
1. 一阶低通滤波器

其传递函数为：$$\frac{Y}{U}=\frac{1}{1+RC\cdot S}$$
其中，滤波器截止频率为${\omega }_c=\frac{1}{RC}$，由$\omega =2\pi f$知，$f_{cut}=\frac{1}{2\pi RC}$

对其进行差分，可得：$$y(k)=\left(1-\frac{\Delta t}{RC}\right)y(k-1)+\frac{\Delta t}{RC}x(k)$$
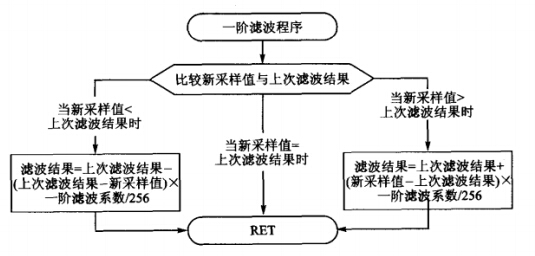
即y[i] = α * x[i] + (1-α) * y[i-1]，其中当α=1时无滤波效果，当α>0.5时在少量上次滤波值的基础上增加相对多量的本次采样值。

Bode图绘制

% 若想滤掉10KHz以上频率，则可令fcut =1k
fcut =1000;
RC=1/2/pi/fcut;
y1 = tf(1,[RC,1])
bode(y1)

2. 一阶高通滤波器

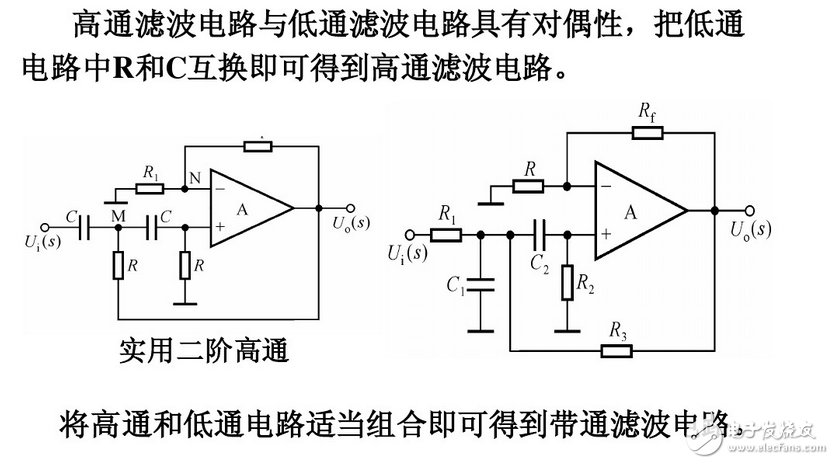
低通滤波器的R和C位置互换即可得到一阶高通滤波器电路模型。

其传递函数为：
$$\frac{Y}{U}=\frac{1}{1+\frac{1}{RC\cdot S}}=\frac{RC\cdot S}{1+RC\cdot S}$$
对其进行差分，可得：
$$y(k)=\frac{RC}{RC+T}y(k-1)+\frac{RC}{RC+T}[x(k)-x(k-1)]$$
即y[i] = α * y[i-1] + α * (x[i] - x[i-1])，其中当α=1时无滤波效果，当α<1时不断弱化上次滤波的值，使采样间的差值相对强化，也就是在不断变弱上次滤波值的基础上增加本次采样值与上次采样值之间的变化。

Bode图绘制

fcut =0.5;
RC=1/2/pi/fcut;
y1 = tf([RC,0],[RC,1])
bode(y1)

3. 互补滤波器

结合一阶低通滤波器和一阶高通滤波器的差分方程可得：
$$y(k)=\frac{RC}{RC+T}\left[y(k-1)+\Delta x(k)\right]+\frac{T}{T+RC}x(k)$$

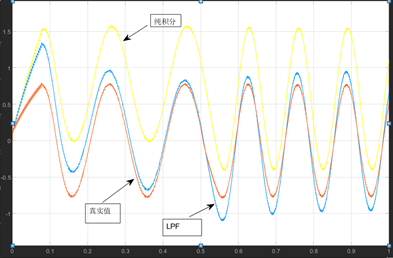
4. Simulink仿真

---

参考文献：

• https://blog.csdn.net/luoshi006/article/details/51459884
• https://blog.csdn.net/qq_27158179/article/details/82661297
• https://blog.csdn.net/qq_38288618/article/details/77049703