前言

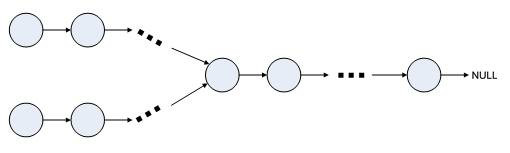
对于环形链表，通过快慢指针，如果存在环，这这两个指针一定会相遇，这是一种经典的判断环或是应用于环问题的思想。

一、案例

1、环形链表

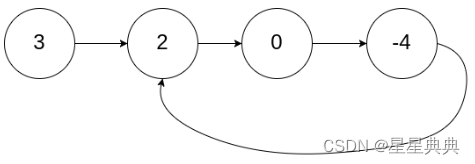
给你一个链表的头节点 head ，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递。仅仅是为了标识链表的实际情况。

如果链表中存在环，则返回 true 。否则，返回 false 。
在这里插入图片描述

注：以O(1)内存进阶。

2、环形链表II

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

注：不允许修改链表。

注：以O(1)内存进阶

二、题解

1、环形链表

1）可以直接遍历，把遍历的结点用Set记录下来，然后记录前查看set中是否有该节点。
2）对于O(1)内存进阶，
A）可以通过修改遍历过的节点的value为一个特殊值，然后一直遍历，如果中途碰到有value为特殊值，说明遍历过，即有环。
B）可每次遍历过之后，就修改前驱节点的next指向为相反的指向，不管是否有环，都不会在遍历中出现死循环，而是从左出即有环，从右出则无环。
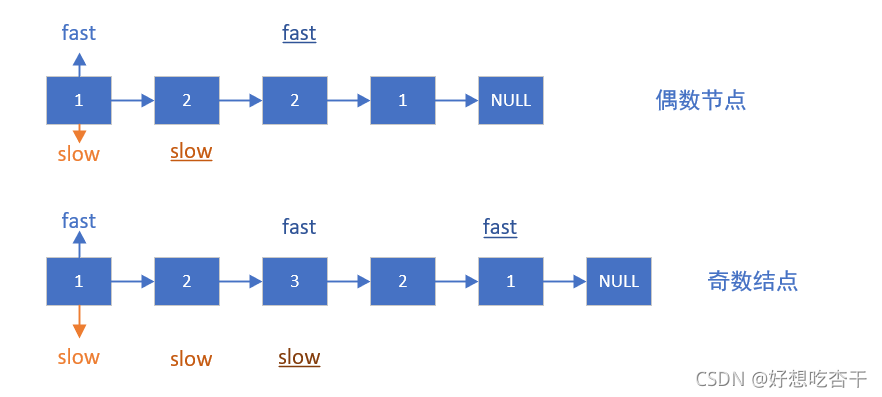
C）快慢指针，可以通过快慢指针，就像在操场跑圈一样，速度快的能和速度慢能相遇。

2、环形链表II

1）从第一个的基础上，1）和2）的A）两种方式上都容易修改得来；而B）不适用；
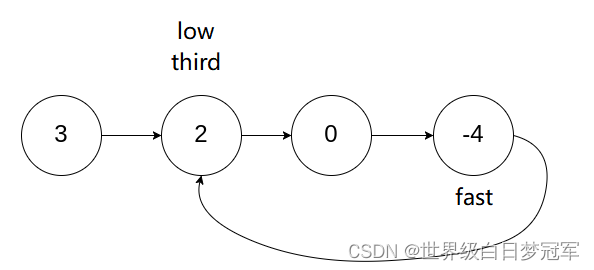
2）对于C），可以得到最后相遇的地方，这个节点一定在环内，设为end节点。外层从头节点遍历到end节点，内层循环从end节点开始遍历，直到下一个end节点，看中途是否会碰到外层循环的中途节点。

3、源码

package com.xhu.offer.tencent;import java.util.HashSet;
import java.util.Set;//环形链表
public class HasCycle {public boolean hasCycle(ListNode head) {//一直next直到next == null 或者next到已经访问过的节点，分别返回true 和 false；Set<ListNode> mark = new HashSet<>();while (head != null) {if (mark.contains(head)) return true;mark.add(head);head = head.next;}return false;}//需要消耗O(1)内存来进阶public boolean hasCycle2(ListNode head) {//每向前走一步就改变链接方向，如果循环结束的最后一个节点是初始节点则有环。if (head == null || head.next == null) return false;ListNode point = head, pre1 = null, pre2;while (point.next != null) {//记录前向节点pre2 = point;//往后遍历point = point.next;//修改前向节点的next指向pre2.next = pre1;//跟新pre1pre1 = pre2;}return point == head;}//修改节点值public boolean hasCycle3(ListNode head) {while (head != null) {if (head.val == Integer.MAX_VALUE) return true;head.val = Integer.MAX_VALUE;head = head.next;}return false;}//快慢指针O(1)public boolean hasCycle4(ListNode head) {//快慢指针，如果有环，则一定会相遇。if (head == null || head.next == null) return false;ListNode point1 = head, point2 = head.next;while (point2 != null) {if (point1 == point2) return true;point1 = point1.next;point2 = point2.next;if (point2 == null) return false;point2 = point2.next;}return false;}//环形链表IIpublic ListNode detectCycle(ListNode head) {//以环形链表I的基础，返回节点即可//一直next直到next == null 或者next到已经访问过的节点Set<ListNode> mark = new HashSet<>();while (head != null) {if (mark.contains(head)) return head;mark.add(head);head = head.next;}return null;}//以O(1)内存进阶public ListNode detectCycle2(ListNode head) {//以环形链表I的基础，返回节点即可//一直next直到next == null 或者next到已经访问过的节点Set<ListNode> mark = new HashSet<>();while (head != null) {if (mark.contains(head)) return head;mark.add(head);head = head.next;}return null;}//以O(1)内存进阶，在不修改链表的情况。public ListNode detectCycle3(ListNode head) {//快慢指针，如果有环，则一定会相遇。这个时候就能确定这个相遇的点一定在环内。//然后从头开始遍历到环内节点，寻找入环节点。if (head == null || head.next == null) return null;ListNode point1 = head, point2 = head.next,end = null;while (point2 != null) {if (point1 == point2) {end = point1;break;}point1 = point1.next;point2 = point2.next;if (point2 == null) return null;point2 = point2.next;}if(end == null) return null;while(head != end){point1 = end.next;while(point1 != end){if(point1 == head) return point1;point1 = point1.next;}head = head.next;}return end;}// Definition for singly-linked list.class ListNode {int val;ListNode next;ListNode(int x) {val = x;next = null;}}
}

4、寻找入环点的数学解法

/*target：找到入环点。快慢指针 找到相遇点，此时起始节点到达相遇点的距离是环长的N倍。设新的起始点在环点，则从此处出发，到达起始点的距离 等于 环点再走n圈一致 - k。而入环点未知，而起始点未知，根据两者关系，反推起始点。*/public ListNode detectCycle(ListNode head) {// bug2：毕竟要先do，所以需要先判断链表是否为null.if (head == null) return null;// bug1:fast = head == null ? null : head.next;这样会导致其先走了一步，导致反推入环口时发生死循环。ListNode slow = head, fast = head;// 寻找相遇点。do {fast = fast.next;slow = slow.next;fast = fast == null ? null : fast.next;} while (slow != fast && fast != null);if (fast == null) return null;// 反推入环点。slow = head;while (slow != fast) {slow = slow.next;fast = fast.next;}return slow;}// Definition for singly-linked list.class ListNode {int val;ListNode next;ListNode(int x) {val = x;next = null;}}
}

// 非do while()
class DetectCycle2 {/*target：找到入环点。快慢指针 找到相遇点，此时起始节点到达相遇点的距离是环长的N倍。设新的起始点在环点，则从此处出发，到达起始点的距离 等于 环点再走n圈一致 - k。而入环点未知，而起始点未知，根据两者关系，反推起始点。*/public ListNode detectCycle(ListNode head) {ListNode slow = head, fast = head == null ? null : head.next;// 寻找相遇点。while (slow != fast && fast != null) {fast = fast.next;slow = slow.next;fast = fast == null ? null : fast.next;}if (fast == null) return null;// 反推入环点。slow = head;fast = fast.next;// a + b + 1 = kNwhile (slow != fast) {slow = slow.next;fast = fast.next;}return slow;}// Definition for singly-linked list.class ListNode {int val;ListNode next;ListNode(int x) {val = x;next = null;}}
}