文章目录
- 版本控制
- Git环境配置
- Git基本理论
- Git项目搭建
- Git文件操作
- 使用码云
- IDEA集成Git
- Git分支
版本控制
版本迭代:每次更新就会有新的版本,旧的版本需要保留。所以我们需要一个版本控制工具帮助我们处理这个问题
版本控制(Revision control)是一种在开发的过程中用于管理我们对文件,目录或工程等内容的修改历史,方便查看更改历史记录,备份以便恢复以前的版本的软件工程技术。
简单说就是用于管理多人协同开发项目的技术。
常见的版本控制工具
主流的版本控制器有如下这些:
- Git(分布式版本控制,没有中央服务器,可以离线提交)
- SVN(集中式版本控制,有中央服务器,不可以离线提交)
- CVS
- VSS
- TFS
- Visual Studio Online
版本控制产品非常多,现在影响力最大 且使用最广泛的Git.
Git下载官网 下载与自己电脑对应的版本即可
安装:无脑下一步即可!安装完毕即可使用了!
启动Git
安装完成后在桌面右击会有Git项

Git Bash:Unix与Linux风格命令行,使用最多,推荐最多
Git CMD:Windows风格命令(这个在安装后的开始菜单Git文件夹下)
Git GUI:图形界面的Git,不建议初学者使用,尽量先属性常用命令
使用Git之前首先要熟悉常用的Linux命令
基本的Linux命令学习

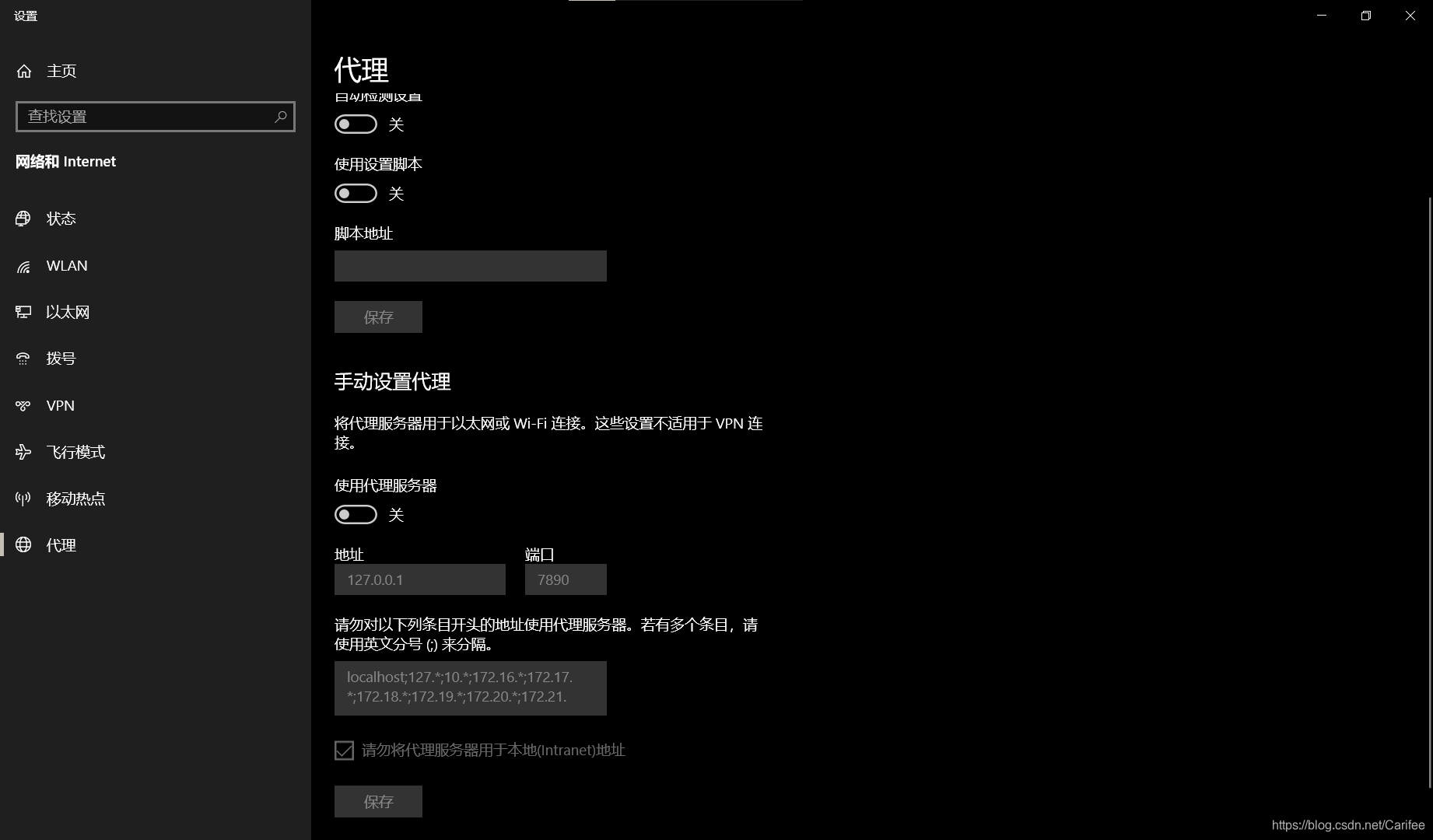
Git环境配置
Git配置
假设在桌面新建一个gitcode文件夹(也可以在桌面直接右击打开,这里为了方便新建了一个空文件进行测试),进入该文件夹右击选择Git Bash选项打开,如下:

查看配置:git config -l

查看其它不同级别的配置文件
#查看系统的config
git config --system --list#查看当前用户(global)配置
git config --global --list
配置用户名和邮箱
当安装Git后首先要做的是设置用户名和邮箱地址,这是非常重要的,因为每次Git提交都会使用该信息,它被永远的嵌入到你的提交中:
#配置用户名
git config --global user.name "xiaolan"#配置邮箱
git config --global user.email 2717110178@qq.com
只需要做一次这样的设置,因为你传递了–global选项,Git将总是使用该信息来处理你系统中所做的一切操作。但如果你希望在不同的项目中使用不同的用户名和邮箱地址,你可以在该项目中运行上面命令时不加–global选项。总之–global为全局配置,不加为某个特定项目的配置。

重新查看配置:git config -l 发现最后两行多出了用户名和邮箱,说明配置成功

到这里GIt就配置完成了,其实就是配置用户名和邮箱而已,环境变量可以配置也可以不配置,配置环境变量是为了在电脑的任何地方都能使用,如通过cmd进行Git操作,当然软件在我们安装的时候它自己已经帮我们配置了。
Git基本理论
工作区域
Git本地有三个工作区域:工作目录(Working Directory),暂存区(Stage/Index),资源库(Repository或Git Directory)。如果再加上远程的git仓库(Remove Directory)就可以分为四个工作区域。文件在这四个区域之间的转换关系如下:

- Workspace:工作区,就是平时存放项目代码的地方
- Index/Stage:暂存区,用于临时存放你的改动,事实上它是一个文件,保存即将提交的列表信息
- local Repository:仓库区(或本地仓库),就是安全存放数据的位置,这里有你提交到所有版本的数据,其中HEAD指向最新放入仓库的版本
- Remote Repository:远程仓库,托管代码的服务器,可以简单的认为是你项目组中的一台电脑用于远程数据交换
以上四个工作区其实跟我们挂钩的只有工作区和远程仓库,暂存区和仓库区我们只需要通过命令操作即可
本都的三个区域确切的说应该是git仓库中HEAD指向的版本:

工作流程
git的工作流程一般是这样的:
-
在工作中添加,修改文件
-
将需要进行的版本管理的文件放入暂存区域
-
将暂存区域文件提交到git仓库
因此,git管理的文件有三种状态:已修改(modified),已暂存(staged),已提交(committed)

Git项目搭建
创建工作目录与常用指令
工作目录(WorkSpace)一般就是你希望Git帮助你管理的文件夹,可以是你的项目目录,也可以是空目录,建议不要有中文。
日常使用只需要记住下图6个命令:

本地仓库搭建
创建本地仓库的方法有两种:一种是创建全新的仓库,另一种是克隆远程仓库。
-
创建全新的仓库,需要用Git管理的项目的根目录执行:
#在当前目录新建一个Git代码库 git init -
执行万命令后可以看到,仅仅在项目目录多出了一个.git目录(注意这个默认是隐藏的文件夹,需要手动在查看选项里面去掉隐藏的文件才能显示),关于版本等所有信息都在这个目录里面

克隆远程仓库
- 另一种方式是克隆远程仓库,由于是将远程服务器上的仓库完全镜像一份至本地!
#克隆一个项目和它的整个代码历史(版本信息)
git clone 链接地址
- 这里以gitee为例,进入gitee官网注册登录后,在里面随便找一个开源项目点进去会有克隆/下载,复制HTTPS下面的链接粘贴到执行上面命令的链接地址即可


这样就克隆完成了,生成的文件夹就是你克隆项目的源代码
Git文件操作
上面j讲的是Git的基本配置和项目搭建,接下来才是关于如何操作文件内容
文件的四种状态
版本控制就是对文件的版本控制,要对文件进行修改,提交等操作,首先要知道文件当前什么状态,不然可能会提交了现在还不想提交的文件,或者要提交的文件没提交上。
- Untracked:未跟踪,此文件在文件夹中,但并没有加入到git仓库,不参与版本控制.通过git add 状态变为Staged.
- Unmodify:文件已经入库,未修改,即版本库中的文件快照内容与文件夹完全一致.这种类型的文件有两种去处,如果它被修改,而变为Modified.如果使用git rm 移出版本库,则成为Untracked文件.
- Modified:文件已修改,仅仅是修改,并没有进行其他的操作.这个文件也有两个去处,通过git add可进入暂存staged状态,使用git checkout,则丢弃修改过,返回unmodify状态,这个git checkout即从库中取出文件,覆盖当前修改!
- Staged:暂存状态,执行git commit则将修改同步到库中,这时库中的文件和本地文件又变为一致,文件为Unmodify状态.执行git reset HEAD filename取消暂存,文件状态为Modified
查看文件状态
上面说的文件的4种状态,通过如下命令可以查看到文件的状态:
#查看制定文件状态
git status [文件名]#查看所有文件状态
git status#添加所有文件到暂存区
git add . #提交暂存区中的内容到本地仓库 -m:提交的信息
git commit -m "信息"
在之前初始化仓库的文件夹中新建一个Hello.txt文件来测试:先执行git status查看文件状态

发现Hello.txt文件未被跟踪,然后我们先执行git add . 命令,再执行git status

发现Hello.txt已经放入暂存区了,等待提交,这时候再执行git commit -m ,最后再一次执行git status查看

发现文件已经提交成功了,没有可提交的文件
忽略文件
有些时候我们不想把某些文件纳入版本控制中,比如数据库文件,临时文件,设计文件等
在主目录下建立“.gitignore”文件,此文件有如下规则:
1.忽略文件中的空行或以井号(# )开始的行将会被忽略。
2.可以使用Linux通配符。例如∶星号(*)代表任意多个字符,问号(﹖)代表一个字符,方括号([abc] )代表可选字符范围,大括号( {string1,string2……})代表可选的字符串等。
3.如果名称的最前面有一个感叹号( !),表示例外规则,将不被忽略。
4.如果名称的最前面是一个路径分隔符(/ ),表示要忽略的文件在此目录下,而子目录中的文件不忽略。
5.如果名称的最后面是一个路径分隔符(/ ),表示要忽略的是此目录下该名称的子目录,而非文件(默认文件或目录都忽略)。
例如以下这些实例:
*.txt #忽略所有的.txt结尾的文件
!lib.txt #但lib.txt除外
/temp #进忽略项目根目录下的TODO文件,不包括其他目录temp
bulid/ #忽略bulid目录下的所有文件
doc/*.txt #会忽略doc/notes.txt 但是不包括doc/sever/arch.txt
使用码云
github是有墙的,比较慢,在国内的话,我们一般使用gitee,公司中有时候会搭建自己的gitlab服务器
-
注册登录码云,完善个人信息
-
设置本机绑定SSH公钥,实现面密码登录!(码云是远程仓库,我们平时工作是在本地仓库,这样每次提交就需要输入密码)
#进入C:\users\Administrator\.ssh 目录,这个目录是在安装git之后就会自动生成的
#生成公钥
ssh-keygen#如果想给公钥进行一些加密则 -t参数为算法类型如
ssh-keygen -t rsa

进入.ssh目录后右击打开Git Bash

刚开始.ssh文件夹是空的,执行命令ssh-keygen然后一路回车到命令执行完毕

执行完命令后会生成上图中的两个文件,公钥位于id_rsa.pub文件(另一个文件是私钥不用管)中,右击记事本打开然后复制粘贴到码云账户上即可

-
使用码云创建一个自己的仓库,根据自己的需求勾选一些属性,下面是我已经创建过了,当然可以创建多个仓库.

-
在本地克隆刚才创建的仓库测试

然后执行命令 git clone 链接地址,发我们自己创建的gitstuday仓库被克隆到本地了


IDEA集成Git
- 新建项目,绑定git
只需把我们刚刚克隆到本地仓库的远程仓库拷贝到新建项目目录中即可





到这里就演示完了IDEA集成Git的基本操作.
Git分支
分支在Git中相对较难,分支就好比科幻电影里面的两个平行世界,如果两个平行世界互不干扰,那对现在的你也没啥影响。不过在某个时间点,两个平行世界合并了,我们就需要解决一些问题了!
总之,多个分支如果并行执行,就会导致我们代码不冲突,也就是同时存在多个版本!

git分支常用命令:
#列出本地所有分支
git branch#列出所有远程分支
git branch -r#新建一个分支,但依然停留在当前分支
git branch 分支名#新建一个分支,并切换到该分支
git checkout -b 分支名#合并指定分支到当前分支
git merge 分支名#删除分支
git branch -d 分支名#删除远程分支
git push origin --delete 分支名
git branch -dr 分支名

如果同一个文件在合并分支时都被修改了则会引起冲突∶解决的办法是我们可以修改冲突文件后重新提交master
主分支应该非常稳定,用来发布新版本,一般情况下不允许在上面工作,工作一般情况下在新建的dev分支,比如上要发布,或者说dev分支代码稳定后可以合并到主分支master上来。