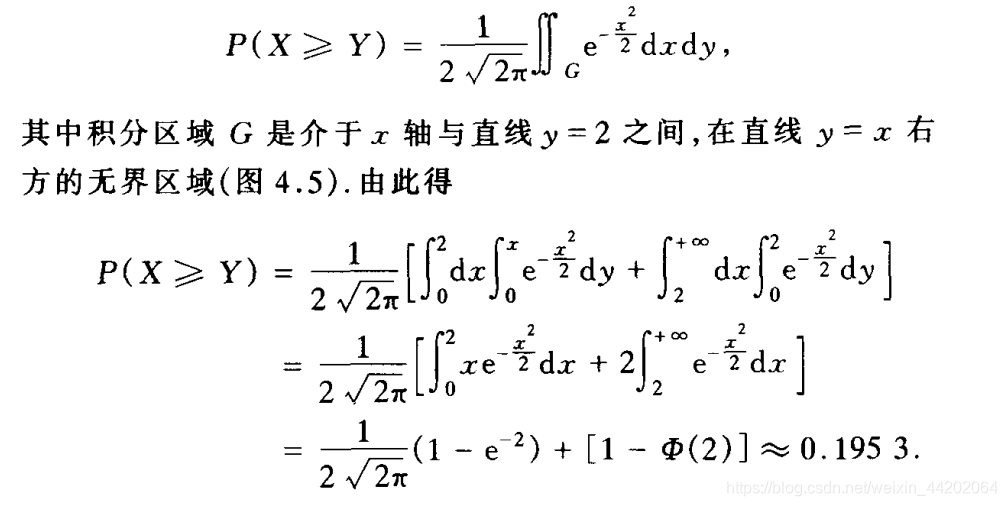利用MATLAB来绘制二维随机变量的联合概率密度图像

article/2025/10/2 3:53:31

本文档通过MATLAB来绘制二维随机变量(X,Y)的联合概率密度函数。
第一种类型，X服从标准正态分布，Y服从均匀分布。
【例题】已知随机变量X与Y相互独立，X~N(0,1);Y在区间[0,2]上服从均匀分布。求：
（1）二维随机变量(X,Y)的联合概率密度。
（2）概率P(X $\geq$ Y)
解答：
（1）随机变量X的概率密度为
$f_{X} (x)=\frac{1}{\sqrt{2\pi} } e^{-\frac{x^2}{2} } -\infty <x<\infty$
随机变量Y的概率密度为
$f_{Y} (y)=\begin{cases} & \frac{1}{2}, y= (0,2)\\ & 0 , y=其它 \end{cases}$
因为X与Y相互独立，所以二维随机变量（X,Y）的联合概率密度为：
$f(x,y)=\begin{cases} & \frac{1}{2\sqrt{2\pi } }e^{-\frac{x^2}{2} }, x=-\infty <x<\infty ,0\le y\le 2 \\ & 0, 其它 \end{cases}$
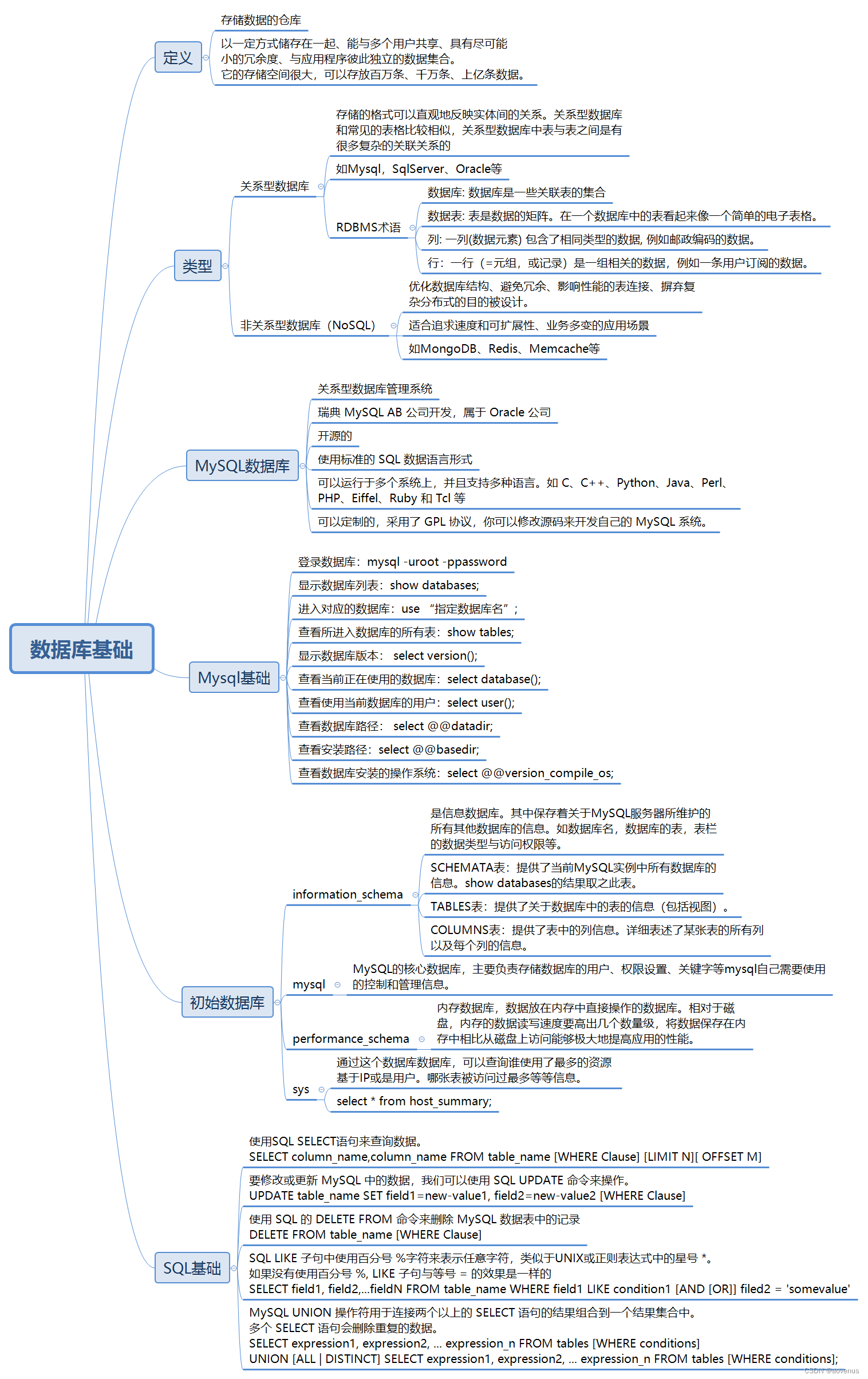
此二维随机变量的联合概率密度函数用MATLAB来绘制，其代码如下
x=-10:0.1:10;
y=0:0.1:1;
z=ones(length(y),1)(exp(-x.^2)/2)/(2sqrt(2*pi));
mesh(x,y,z)
输出图像为
在这里插入图片描述
（2）概率P(X $\geq$ Y)就是随机点(X,Y)落在平面区域X $\geq$ Y内的概率。

第二种类型：X与Y均服从正态分布，且不独立。
【例题】设二维随机变量（X,Y）的联合概率密度函数为
$f\left ( x,y \right ) =\frac{5}{96\pi }e ^{-\frac{25}{32}\left [ \frac{\left ( x-1\right )^{2} }{9} +\frac{\left ( x-1 \right )\left ( y-2 \right ) }{10}+\frac{\left ( y-2 \right )^2 }{16} \right ] }$
（1）例用MATLAB画出联合密度函数图
（2）求随机变量函数Z=X/3-Y/4的数学期望和方差
【解答】
（1）根据二维随机变量(X,Y)服从二维正态分布的概率函数
$f\left ( x,y \right ) =\frac{1}{2\pi\sigma _{x}\sigma _{y}\sqrt{1-r^2} }e ^{-\frac{1}{2\left ( 1-r^2 \right ) }\left [ \frac{\left ( x-\mu _{x} \right )^{2} }{\sigma _{x}^2 } +\frac{2r\left ( x-\mu _{x} \right )\left ( y-\mu _{y} \right ) }{\sigma _{x} \sigma _{y} } +\frac{\left ( y-\mu _{y} \right )^2 }{\sigma _{y}^{2} } \right ] }$
记作：
$\left ( X,Y \right ) \sim N\left ( \mu _{X} ,\mu _{Y} ,\sigma _{X}^2,\sigma _{Y}^2,r \right )$ r的绝对值小于1.
可知， $E\left ( X \right ) =1,E\left ( Y \right ) =2,D\left ( X \right ) =9,D\left ( Y \right ) =16,R(X,Y)=r=-\frac{3}{5}$
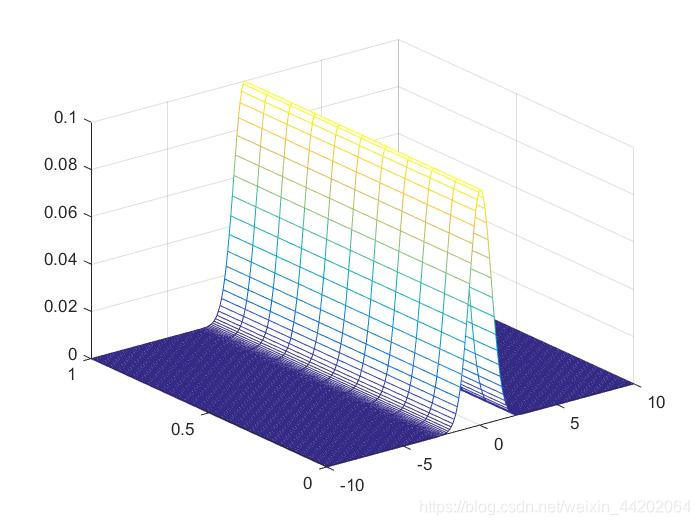
程序代码为：
clc;
clear;
x=-4:0.1:6;
y=-3:0.1:7;
[X,Y]=meshgrid(x,y);
Z=5exp(-25((X-1).^{2+(X-1).*(Y-2)/10+(Y-2).}2/16)/32)/(96*pi);
mesh(X,Y,Z); %绘制三维网格图

运行后三维网格图的图像为：
在这里插入图片描述
（2） $cov\left ( X,Y \right ) =R\left ( X,Y \right ) \sigma _{x} \sigma _{y}=-\frac{36}{5}$
$E\left ( Z \right ) =E\left ( \frac{X}{3}-\frac{Y}{4} \right ) =-\frac{1}{6}$
$D\left ( Z \right ) =D\left ( \frac{X}{3} -\frac{Y}{4} \right ) =\left ( \frac{1}{3} \right )^2D\left ( X \right ) +\left ( -\frac{1}{4}^2D\left ( Y \right ) \right ) +2\times \frac{1}{4}\times \left ( -\frac{1}{4} \right ) =\frac{16}{5}$
第三种类型：X与Y均服从标准正态分布，且相互独立
【例题】设随机变量X与Y相互独立，都服从标准正态分布N（0，1），求：
（1）画出该二维随机变量的联合概率密度函数图像。
（2）求出随机变量函数 $Z=X^{2} +Y^{2}$ 的概率密度
【解答】
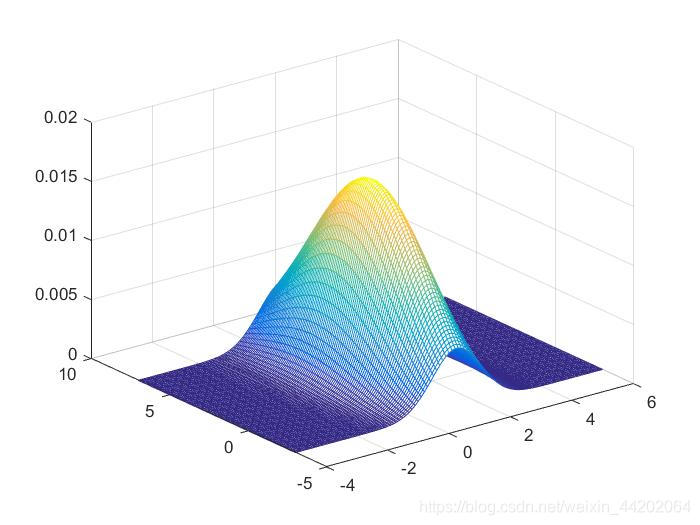
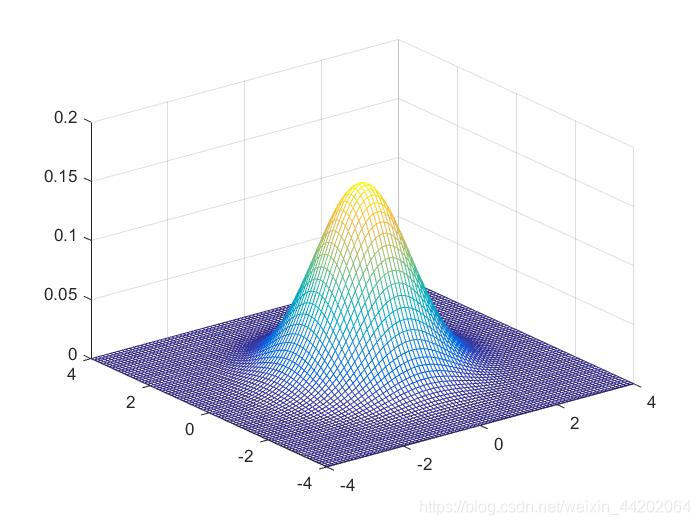
（1）相互独立的二维随机变量X与Y的联合概率密度函数为
$f\left ( x,y \right ) =f_X\left ( x \right ) f_Y\left ( y \right ) =\frac{1}{2\pi }e^{-\frac{x^2+y^2}{2} }$
绘制该函数用到的代码为：
vx=-4:0.1:4;
[X,Y]=meshgrid(vx);
Z=exp(-(X.^2+Y.2)/2)/(2*pi);
mesh(X,Y,Z);
绘制的联合概率密度图像为
XY独立且服从标准正态分布
（2）随机变量 $Z=X^{2} +Y^{2}$ 的分布函数为
$F_{Z} \left ( z \right ) =P\left ( Z\le z \right ) =P\left ( X^2+Y^2\le z \right ) =\iint\limits_{x^2+y^2\le z}^{} e^{-\frac{x^2+y^2}{2} dxdy} =1-e^{\frac{z}{2} }$
所以Z的分布函数为
$F_{Z} \left ( z \right ) =\begin{cases} & 1-e^{-\frac{z}{2} }, { } z>0 \\ & 0,{ } z\le 0 \end{cases}$
例用matlab绘制图像为

程序代码为
fplot(@(z)1-exp(-z/2),[0,10]);
由Z的分布函数得Z的概率密度函数为
$f_{Z} \left ( z \right ) =\begin{cases} & \frac{1}{2}e^{-\frac{z}{2} }, { } z>0 \\ & 0,{ } z\le 0 \end{cases}$
例用Matlab绘制图像为

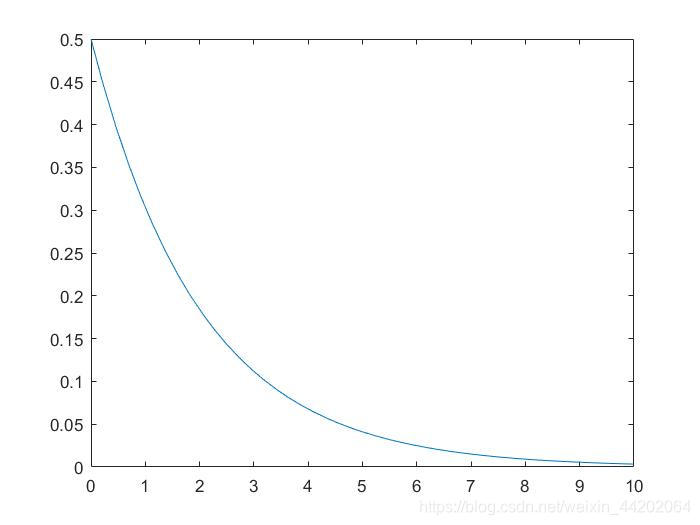
程序代码为 fplot(@(z)exp(-z/2)/2,[0,10]);
此时，Z的随机变量函数服从的分布是自由度为2的 $\chi ^{2}$ 分布