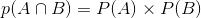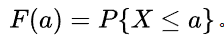离散随机变量的联合分布
我们先从离散的情况出发,了解多个随机变量并存的含义。
之前说,一个随机变量是从样本空间到实数的映射。然而,所谓的映射是人为创造的。从一个样本空间,可以同时产生多个映射。比如,我们的实验是连续三次投硬币,样本空间为
h为正面,t为反面。在同一样本空间上,我们可以定义多个随机变量,比如:
- X X: 投掷为正面的总数,可以取值0,1,2,3
- Y Y: 最后一次出现负面的总数,可以取值0,1
- Z Z: 将正面记为10,负面记为5,第一次与第三次取值的差,可以有5, -5, 0
这三个随机变量可以看作一个有三个分量的矢量。所以定义在同一样本空间的多随机变量,是一个从样本空间到矢量的映射。
(从这个角度上说,单一随机变量是一个从样本空间到一个有一个分量的矢量的映射)
如果样本空间 Ω Ω中每个结果出现的概率相等。而样本空间中共有8个结果,那么个每个结果的出现的概率都是1/8。据此,我们可以计算联合概率,比如
对于 X=x,Y=y X=x,Y=y,我们寻找样本空间中满足这两个取值的所有元素。这些元素构成一个样本空间的子集,该子集的概率就是 P(X=x,Y=y) P(X=x,Y=y)的联合概率。 p(x,y)=P(X=x,Y=y) p(x,y)=P(X=x,Y=y)称为联合概率质量函数(joint PMF, joint probability mass function)。联合概率可以看做两个事件同时发生时的概率,事件A为 X=x X=x,事件B为 Y=y Y=y,即 P(A∩B) P(A∩B)。
找到所有可能取值组合的概率,就找到了这两个随机变量的联合分布:
| X X | Y Y | P(X,Y) P(X,Y) | 对应子集 |
| 0 | 0 | 0 | Φ Φ |
| 1 | 0 | 1/8 | tth |
| 2 | 0 | 2/8 | thh, hth |
| 3 | 0 | 1/8 | hhh |
| 0 | 1 | 1/8 | ttt |
| 1 | 1 | 2/8 | htt, tht |
| 2 | 1 | 1/8 | hht |
| 3 | 1 | 0 | Φ Φ |
联合分布
联合分布描述了所有可能的取值情况。因此,联合概率密度函数的累积和为1。
连续随机变量的联合分布
我们知道,单个连续随机变量的概率是变量在某个区间(某段线的“长度”)取值的概率。做类似的推广,多个连续随机变量的概率,是这多个随机变量在多维区间的概率。比如两个随机变量,我们需要表达一个二维区间的概率,比如 P(a≤X≤b,c≤Y≤d) P(a≤X≤b,c≤Y≤d)。这个二维区间可以有一个类似于一个小补丁的“面积”。二维区间对应的概率是一个体积。

面积对应的体积
在单变量情况下,概率是一个“面积”,是由区间的“长度”和密度函数(一条曲线)围成的。这里的“体积”是二维区间的“面积”和密度函数(一个曲面)围成的。我们可以使用联合概率密度函数(joint PDF, joint probability density function)来表达多随机变量的分布。对于双变量的联合分布来说,它等于无穷小块的概率,除以无穷小块的面积。
用微积分的语言来说,就是
f(x,y) f(x,y)就是描述X和Y的联合分布的联合概率密度函数。
联合概率密度函数描述了所有可能取值的情况,因此有
实例
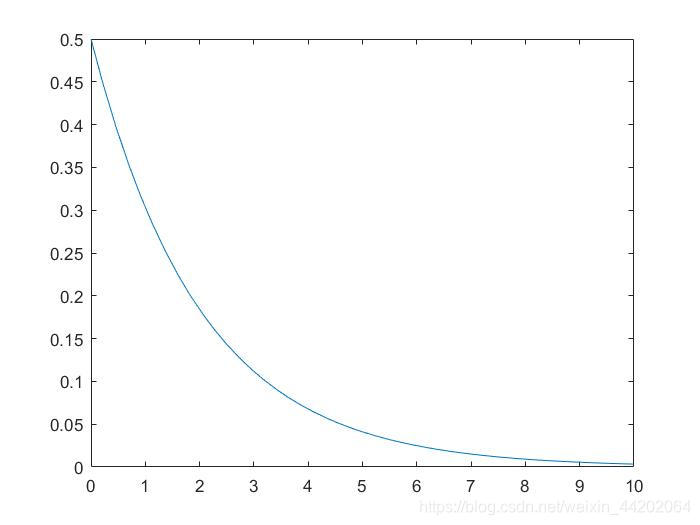
下面是两个连续随机变量的联合PDF:
通过积分,计算X在0到0.5,而Y在0到1的概率:
我们之间也说到,单个随机变量的概率对应线段到概率密度曲线之间的面积。而两个随机变量的概率对应小块到概率密度面之间的体积。
我们可以绘制 f(x,y) f(x,y)的分布图形,即一个二维的平面。图中的颜色标记了f(x, y)值的大小。如下:
 可以看到,f(x, y)随X增大而增大,在X值确定时,f(x, y)不随Y变化。
可以看到,f(x, y)随X增大而增大,在X值确定时,f(x, y)不随Y变化。
边缘概率
联合分布包含了多个随机变量的分布信息。我们当然可以从联合分布中,提取出任意一个单一随机变量的分布,也就是所谓的边缘分布(marginal distribution)。
对于离散随机变量,可以获得边缘概率质量函数(marginal pmf):
在求X的单一边缘分布时, 我们累加了相同x值、不同y值时的多个联合概率,从而获得该x值的的总体概率,即边缘概率。
连续随机变量X的边缘密度函数(marginal pdf, marginal probability density function)可以定义为
fX(x) fX(x)是联合密度函数对Y的积分。通过积分,我们将不同Y取值时的联合概率加在一起,就获得纯粹的单一X的分布状况。
类似的,Y的边缘密度函数为
取离散随机分布的例子,即掷三次硬币
| 0 | 1 | 2 | 3 | p(y) | |
| 0 | 0 | 1/8 | 2/8 | 1/8 | 1/2 |
| 1 | 1/8 | 2/8 | 1/8 | 0 | 1/2 |
| p(x) | 1/8 | 3/8 | 3/8 | 1/8 |
边缘概率是对各行和列的累加。最后一列p(y)是Y的分布,Y有1/2的概率取0,1/2的概率取1。最后一行p(x)是X的分布。
取连续随机分布的例子,即下面的连续分布:
可以得到:
条件分布
我们之前基于事件介绍了条件概率,即如果事件B发生,那么事件A发生的概率。相同的概念可以引申到随机变量。随机变量取某个值,这可以看做一个事件。我们想知道,随机变量Y取值y,另一个随机变量X为x的概率。
与事件的条件概率类似,假设 pY(y)≠0 pY(y)≠0,在 Y=y Y=y的条件下,随机变量X取值为x的概率定义为:
即 X=x,Y=y X=x,Y=y同时发生的概率,除以Y取值为y的的概率。
以掷三次硬币为例。条件为Y值取值0,即最后一次投掷为正面时。此时,X取值为2有两种可能,即前两次为ht和th。由于前两次投掷有四种组合,所以概率为0.5。
我们可以通过条件概率的公式计算并验证:
如果说概率是分一个总和为1的大饼,如果大饼分八块,每块就是1/8。假设半个饼上撒胡椒,另半个饼上撒辣椒。那么在胡椒饼(相当于我们的条件)上选取一块的概率,就是1/4。此时,也就是用原来的概率除以胡椒饼所占的比重。
对于连续随机变量,假设 fY(y)≠0 fY(y)≠0,给定Y=y,随机变量X的条件分布为:
独立随机变量
正如事件之间可以相互独立一样,随机变量之间也可以相互独立。当X独立于Y时,我们可以相像,Y的取值,将不影响X的概率。也就是说
这意味着,当且仅当
时,X和Y相互独立。
可以验证,连续投掷三次硬币的例子中,X和Y并不独立,比如
因此,
X和Y并不独立。
对于连续随机变量来说,当且仅当
时,X和Y相互独立。
对于分布
使用之前获得的边际分布,可以验证
因此,对于该分布来说,X和Y相互独立。