机器学习——决策树算法

article/2025/11/11 1:42:57

文章目录

  • 一、决策树介绍
  • 二、利用信息增益选择最优划分属性
  • 三、ID3代码实现
    • 1.jupyter下python实现
    • 2. 使用sklearn实现ID3
  • 四、C4.5算法实现
  • 五、CART算法实现
  • 六、总结
  • 参考文献

一、决策树介绍

  • 决策树是一种基于树结构来进行决策的分类算法，我们希望从给定的训练数据集学得一个模型（即决策树），用该模型对新样本分类。决策树可以非常直观展现分类的过程和结果，一旦模型构建成功，对新样本的分类效率也相当高。

  • 最经典的决策树算法有ID3、C4.5、CART，其中ID3算法是最早被提出的，它可以处理离散属性样本的分类，C4.5和CART算法则可以处理更加复杂的分类问题。使用算法ID3, C4.5和C5.0生成树算法使用熵。这一度量是基于信息学理论中熵的概念。

  • 分类树（决策树）是一种十分常用的分类方法。它是一种监督学习，所谓监督学习就是给定一堆样本，每个样本都有一组属性和一个类别，这些类别是事先确定的，那么通过学习得到一个分类器，这个分类器能够对新出现的对象给出正确的分类。这样的机器学习就被称之为监督学习。

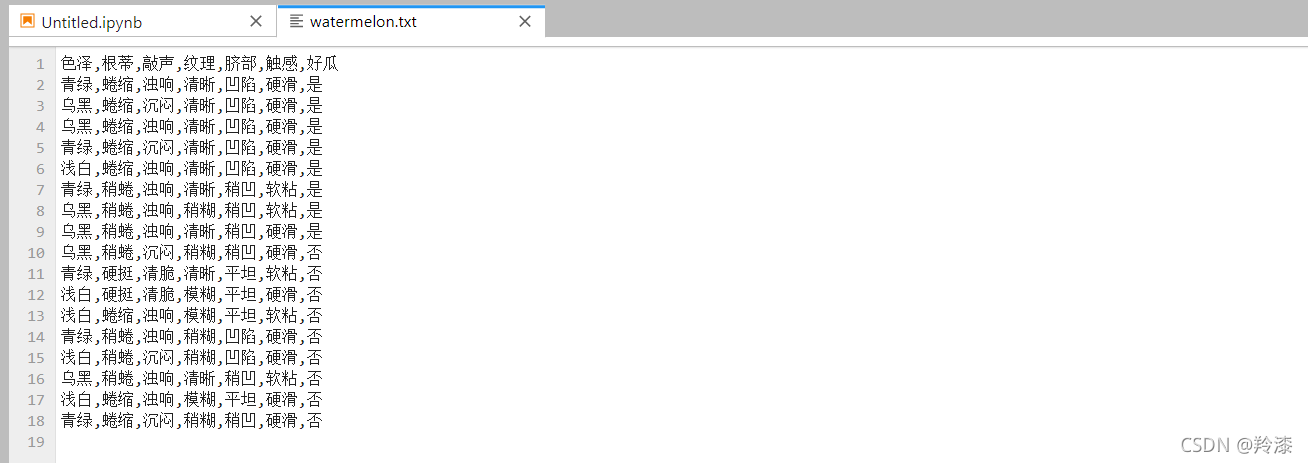
  • 下面，我们就对以下表格中的西瓜样本构建决策树模型。

色泽根蒂敲声纹理脐部触感好瓜
青绿蜷缩浊响清晰凹陷硬滑是
乌黑蜷缩沉闷清晰凹陷硬滑是
乌黑蜷缩浊响清晰凹陷硬滑是
青绿蜷缩沉闷清晰凹陷硬滑是
浅白蜷缩浊响清晰凹陷硬滑是
青绿稍蜷浊响清晰稍凹软粘是
乌黑稍蜷浊响稍糊稍凹软粘是
乌黑稍蜷浊响清晰稍凹硬滑是
乌黑稍蜷沉闷稍糊稍凹硬滑否
青绿硬挺清脆清晰平坦软粘否
浅白硬挺清脆模糊平坦硬滑否
浅白蜷缩浊响模糊平坦软粘否
青绿稍蜷浊响稍糊凹陷硬滑否
浅白稍蜷沉闷稍糊凹陷硬滑否
乌黑稍蜷浊响清晰稍凹软粘否
浅白蜷缩浊响模糊平坦硬滑否
青绿蜷缩沉闷稍糊稍凹硬滑否

二、利用信息增益选择最优划分属性

样本有多个属性，该先选哪个样本来划分数据集呢？原则是随着划分不断进行，我们希望决策树的分支节点所包含的样本尽可能属于同一分类，即“纯度”越来越高。

  • 信息熵
    所谓信息熵，是一个数学上颇为抽象的概念，在这里不妨把信息熵理解成某种特定信息的出现概率。
    样本集合D中第k类样本所占的比例p_k（k=1,2,…,|Y|），|Y|为样本分类的个数，则D的信息熵为：
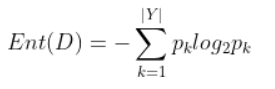
    在这里插入图片描述
    Ent(D)的值越小，则D的纯度越高。
  • 信息增益
    使用属性a对样本集D进行划分所获得的“信息增益”的计算方法是，用样本集的总信息熵减去属性a的每个分支的信息熵与权重（该分支的样本数除以总样本数）的乘积，通常，信息增益越大，意味着用属性a进行划分所获得的“纯度提升”越大。因此，优先选择信息增益最大的属性来划分。
    西瓜样本集中，以属性“色泽”为例，它有3个取值{青绿、乌黑、浅白}
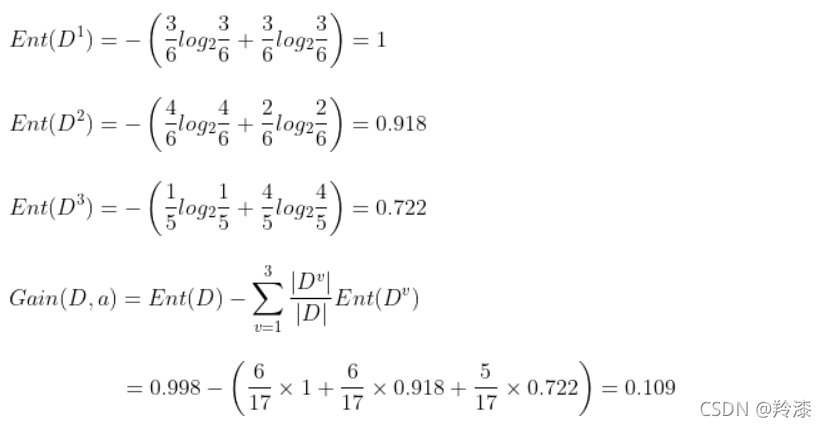
    在这里插入图片描述
    同理也可以计算出其他几个属性的信息增益，选择信息增益最大的属性作为根节点来进行划分，然后再对每个分支做进一步划分。

三、ID3代码实现

在代码路径下新建watermelon.txt文件
在这里插入图片描述

1.jupyter下python实现

  • 导入模块
    用pandas模块的read_csv()函数读取数据文本；用numpy模块将dataframe转换为list（列表）；用Counter来完成计数；用math模块的log2函数计算对数。
#导入模块
import numpy as np
import pandas as pd
import math
import collections
  • 导入数据
def import_data():data = pd.read_csv('..watermelon.txt')data.head(10)data=np.array(data).tolist()# 特征值列表labels = ['色泽', '根蒂', '敲击', '纹理', '脐部', '触感']# 特征对应的所有可能的情况labels_full = {}for i in range(len(labels)):labelList = [example[i] for example in data]uniqueLabel = set(labelList)labels_full[labels[i]] = uniqueLabelreturn data,labels,labels_full
  • 调用函数获取数据
data,labels,labels_full=import_data()
  • 计算初始的信息熵，就是不分类之前的信息熵值
def calcShannonEnt(dataSet):"""计算给定数据集的信息熵(香农熵):param dataSet::return:"""# 计算出数据集的总数numEntries = len(dataSet)# 用来统计标签labelCounts = collections.defaultdict(int)# 循环整个数据集，得到数据的分类标签for featVec in dataSet:# 得到当前的标签currentLabel = featVec[-1]# # 如果当前的标签不再标签集中，就添加进去（书中的写法）# if currentLabel not in labelCounts.keys():#     labelCounts[currentLabel] = 0## # 标签集中的对应标签数目加一# labelCounts[currentLabel] += 1# 也可以写成如下labelCounts[currentLabel] += 1# 默认的信息熵shannonEnt = 0.0for key in labelCounts:# 计算出当前分类标签占总标签的比例数prob = float(labelCounts[key]) / numEntries# 以2为底求对数shannonEnt -= prob * math.log2(prob)return shannonEnt
  • 查看初始信息熵
print(calcShannonEnt(data)) # 输出为：0.9975025463691153

在这里插入图片描述

  • 获取每个特征值的数量，这是为后面计算信息增益做准备
def splitDataSet(dataSet, axis, value):"""按照给定的特征值，将数据集划分:param dataSet: 数据集:param axis: 给定特征值的坐标:param value: 给定特征值满足的条件，只有给定特征值等于这个value的时候才会返回:return:"""# 创建一个新的列表，防止对原来的列表进行修改retDataSet = []# 遍历整个数据集for featVec in dataSet:# 如果给定特征值等于想要的特征值if featVec[axis] == value:# 将该特征值前面的内容保存起来reducedFeatVec = featVec[:axis]# 将该特征值后面的内容保存起来，所以将给定特征值给去掉了reducedFeatVec.extend(featVec[axis + 1:])# 添加到返回列表中retDataSet.append(reducedFeatVec)return retDataSet
  • 计算信息增益来确定最好的数据集划分
def chooseBestFeatureToSplit(dataSet, labels):"""选择最好的数据集划分特征，根据信息增益值来计算:param dataSet::return:"""# 得到数据的特征值总数numFeatures = len(dataSet[0]) - 1# 计算出基础信息熵baseEntropy = calcShannonEnt(dataSet)# 基础信息增益为0.0bestInfoGain = 0.0# 最好的特征值bestFeature = -1# 对每个特征值进行求信息熵for i in range(numFeatures):# 得到数据集中所有的当前特征值列表featList = [example[i] for example in dataSet]# 将当前特征唯一化，也就是说当前特征值中共有多少种uniqueVals = set(featList)# 新的熵，代表当前特征值的熵newEntropy = 0.0# 遍历现在有的特征的可能性for value in uniqueVals:# 在全部数据集的当前特征位置上，找到该特征值等于当前值的集合subDataSet = splitDataSet(dataSet=dataSet, axis=i, value=value)# 计算出权重prob = len(subDataSet) / float(len(dataSet))# 计算出当前特征值的熵newEntropy += prob * calcShannonEnt(subDataSet)# 计算出“信息增益”infoGain = baseEntropy - newEntropy#print('当前特征值为：' + labels[i] + '，对应的信息增益值为：' + str(infoGain)+"i等于"+str(i))#如果当前的信息增益比原来的大if infoGain > bestInfoGain:# 最好的信息增益bestInfoGain = infoGain# 新的最好的用来划分的特征值bestFeature = i#print('信息增益最大的特征为：' + labels[bestFeature])return bestFeature
  • 判断各个样本集的各个属性是否一致
def judgeEqualLabels(dataSet):"""判断数据集的各个属性集是否完全一致:param dataSet::return:"""# 计算出样本集中共有多少个属性，最后一个为类别feature_leng = len(dataSet[0]) - 1# 计算出共有多少个数据data_leng = len(dataSet)# 标记每个属性中第一个属性值是什么first_feature = ''# 各个属性集是否完全一致is_equal = True# 遍历全部属性for i in range(feature_leng):# 得到第一个样本的第i个属性first_feature = dataSet[0][i]# 与样本集中所有的数据进行对比，看看在该属性上是否都一致for _ in range(1, data_leng):# 如果发现不相等的，则直接返回Falseif first_feature != dataSet[_][i]:return Falsereturn is_equal
  • 绘制决策树（字典）
def createTree(dataSet, labels):"""创建决策树:param dataSet: 数据集:param labels: 特征标签:return:"""# 拿到所有数据集的分类标签classList = [example[-1] for example in dataSet]# 统计第一个标签出现的次数，与总标签个数比较，如果相等则说明当前列表中全部都是一种标签，此时停止划分if classList.count(classList[0]) == len(classList):return classList[0]# 计算第一行有多少个数据，如果只有一个的话说明所有的特征属性都遍历完了，剩下的一个就是类别标签，或者所有的样本在全部属性上都一致if len(dataSet[0]) == 1 or judgeEqualLabels(dataSet):# 返回剩下标签中出现次数较多的那个return majorityCnt(classList)# 选择最好的划分特征，得到该特征的下标bestFeat = chooseBestFeatureToSplit(dataSet=dataSet, labels=labels)print(bestFeat)# 得到最好特征的名称bestFeatLabel = labels[bestFeat]print(bestFeatLabel)# 使用一个字典来存储树结构，分叉处为划分的特征名称myTree = {bestFeatLabel: {}}# 将本次划分的特征值从列表中删除掉del(labels[bestFeat])# 得到当前特征标签的所有可能值featValues = [example[bestFeat] for example in dataSet]# 唯一化，去掉重复的特征值uniqueVals = set(featValues)# 遍历所有的特征值for value in uniqueVals:# 得到剩下的特征标签subLabels = labels[:]subTree = createTree(splitDataSet(dataSet=dataSet, axis=bestFeat, value=value), subLabels)# 递归调用，将数据集中该特征等于当前特征值的所有数据划分到当前节点下，递归调用时需要先将当前的特征去除掉myTree[bestFeatLabel][value] = subTreereturn myTree
  • 调用函数并打印，就可以看到一个字典类型的树了
mytree=createTree(data,labels)
print(mytree)

在这里插入图片描述

  • 绘制可视化树
import matplotlib.pylab as plt
import matplotlib# 能够显示中文
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['font.serif'] = ['SimHei']# 分叉节点，也就是决策节点
decisionNode = dict(boxstyle="sawtooth", fc="0.8")# 叶子节点
leafNode = dict(boxstyle="round4", fc="0.8")# 箭头样式
arrow_args = dict(arrowstyle="<-")def plotNode(nodeTxt, centerPt, parentPt, nodeType):"""绘制一个节点:param nodeTxt: 描述该节点的文本信息:param centerPt: 文本的坐标:param parentPt: 点的坐标，这里也是指父节点的坐标:param nodeType: 节点类型,分为叶子节点和决策节点:return:"""createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',xytext=centerPt, textcoords='axes fraction',va="center", ha="center", bbox=nodeType, arrowprops=arrow_args)def getNumLeafs(myTree):"""获取叶节点的数目:param myTree::return:"""# 统计叶子节点的总数numLeafs = 0# 得到当前第一个key，也就是根节点firstStr = list(myTree.keys())[0]# 得到第一个key对应的内容secondDict = myTree[firstStr]# 递归遍历叶子节点for key in secondDict.keys():# 如果key对应的是一个字典，就递归调用if type(secondDict[key]).__name__ == 'dict':numLeafs += getNumLeafs(secondDict[key])# 不是的话，说明此时是一个叶子节点else:numLeafs += 1return numLeafsdef getTreeDepth(myTree):"""得到数的深度层数:param myTree::return:"""# 用来保存最大层数maxDepth = 0# 得到根节点firstStr = list(myTree.keys())[0]# 得到key对应的内容secondDic = myTree[firstStr]# 遍历所有子节点for key in secondDic.keys():# 如果该节点是字典，就递归调用if type(secondDic[key]).__name__ == 'dict':# 子节点的深度加1thisDepth = 1 + getTreeDepth(secondDic[key])# 说明此时是叶子节点else:thisDepth = 1# 替换最大层数if thisDepth > maxDepth:maxDepth = thisDepthreturn maxDepthdef plotMidText(cntrPt, parentPt, txtString):"""计算出父节点和子节点的中间位置，填充信息:param cntrPt: 子节点坐标:param parentPt: 父节点坐标:param txtString: 填充的文本信息:return:"""# 计算x轴的中间位置xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]# 计算y轴的中间位置yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]# 进行绘制createPlot.ax1.text(xMid, yMid, txtString)def plotTree(myTree, parentPt, nodeTxt):"""绘制出树的所有节点，递归绘制:param myTree: 树:param parentPt: 父节点的坐标:param nodeTxt: 节点的文本信息:return:"""# 计算叶子节点数numLeafs = getNumLeafs(myTree=myTree)# 计算树的深度depth = getTreeDepth(myTree=myTree)# 得到根节点的信息内容firstStr = list(myTree.keys())[0]# 计算出当前根节点在所有子节点的中间坐标,也就是当前x轴的偏移量加上计算出来的根节点的中心位置作为x轴（比如说第一次：初始的x偏移量为：-1/2W,计算出来的根节点中心位置为：(1+W)/2W，相加得到：1/2），当前y轴偏移量作为y轴cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)# 绘制该节点与父节点的联系plotMidText(cntrPt, parentPt, nodeTxt)# 绘制该节点plotNode(firstStr, cntrPt, parentPt, decisionNode)# 得到当前根节点对应的子树secondDict = myTree[firstStr]# 计算出新的y轴偏移量，向下移动1/D，也就是下一层的绘制y轴plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD# 循环遍历所有的keyfor key in secondDict.keys():# 如果当前的key是字典的话，代表还有子树，则递归遍历if isinstance(secondDict[key], dict):plotTree(secondDict[key], cntrPt, str(key))else:# 计算新的x轴偏移量，也就是下个叶子绘制的x轴坐标向右移动了1/WplotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW# 打开注释可以观察叶子节点的坐标变化# print((plotTree.xOff, plotTree.yOff), secondDict[key])# 绘制叶子节点plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)# 绘制叶子节点和父节点的中间连线内容plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))# 返回递归之前，需要将y轴的偏移量增加，向上移动1/D，也就是返回去绘制上一层的y轴plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalDdef createPlot(inTree):"""需要绘制的决策树:param inTree: 决策树字典:return:"""# 创建一个图像fig = plt.figure(1, facecolor='white')fig.clf()axprops = dict(xticks=[], yticks=[])createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)# 计算出决策树的总宽度plotTree.totalW = float(getNumLeafs(inTree))# 计算出决策树的总深度plotTree.totalD = float(getTreeDepth(inTree))# 初始的x轴偏移量，也就是-1/2W，每次向右移动1/W，也就是第一个叶子节点绘制的x坐标为：1/2W，第二个：3/2W，第三个：5/2W，最后一个：(W-1)/2WplotTree.xOff = -0.5/plotTree.totalW# 初始的y轴偏移量，每次向下或者向上移动1/DplotTree.yOff = 1.0# 调用函数进行绘制节点图像plotTree(inTree, (0.5, 1.0), '')# 绘制plt.show()if __name__ == '__main__':createPlot(mytree)

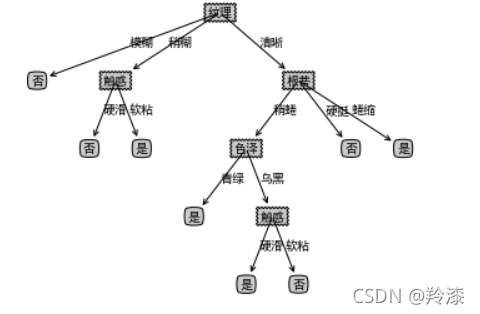
在这里插入图片描述

  • 这里树少了一些标签，需要补全树之后再次输出
def makeTreeFull(myTree, labels_full, default):"""将树中的不存在的特征标签进行补全，补全为父节点中出现最多的类别:param myTree: 生成的树:param labels_full: 特征的全部标签:param parentClass: 父节点中所含最多的类别:param default: 如果缺失标签中父节点无法判断类别则使用该值:return:"""# 这里所说的父节点就是当前根节点，把当前根节点下不存在的特征标签作为子节点# 拿到当前的根节点root_key = list(myTree.keys())[0]# 拿到根节点下的所有分类，可能是子节点（好瓜or坏瓜）也可能不是子节点（再次划分的属性值）sub_tree = myTree[root_key]# 如果是叶子节点就结束if isinstance(sub_tree, str):return# 找到使用当前节点分类下最多的种类，该分类结果作为新特征标签的分类，如：色泽下面没有浅白则用色泽中有的青绿分类作为浅白的分类root_class = []# 把已经分好类的结果记录下来for sub_key in sub_tree.keys():if isinstance(sub_tree[sub_key], str):root_class.append(sub_tree[sub_key])# 找到本层出现最多的类别，可能会出现相同的情况取其一if len(root_class):most_class = collections.Counter(root_class).most_common(1)[0][0]else:most_class = None# 当前节点下没有已经分类好的属性# print(most_class)# 循环遍历全部特征标签，将不存在标签添加进去for label in labels_full[root_key]:if label not in sub_tree.keys():if most_class is not None:sub_tree[label] = most_classelse:sub_tree[label] = default# 递归处理for sub_key in sub_tree.keys():if isinstance(sub_tree[sub_key], dict):makeTreeFull(myTree=sub_tree[sub_key], labels_full=labels_full, default=default)

调用并再次绘制树

makeTreeFull(mytree,labels_full,default='未知')
createPlot(mytree)

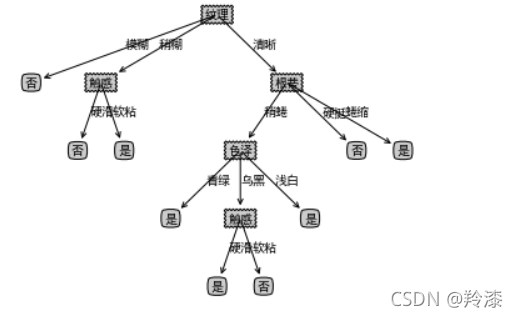
在这里插入图片描述

2. 使用sklearn实现ID3

  • 导入包
# 导入包
import pandas as pd
from sklearn import tree
import graphviz
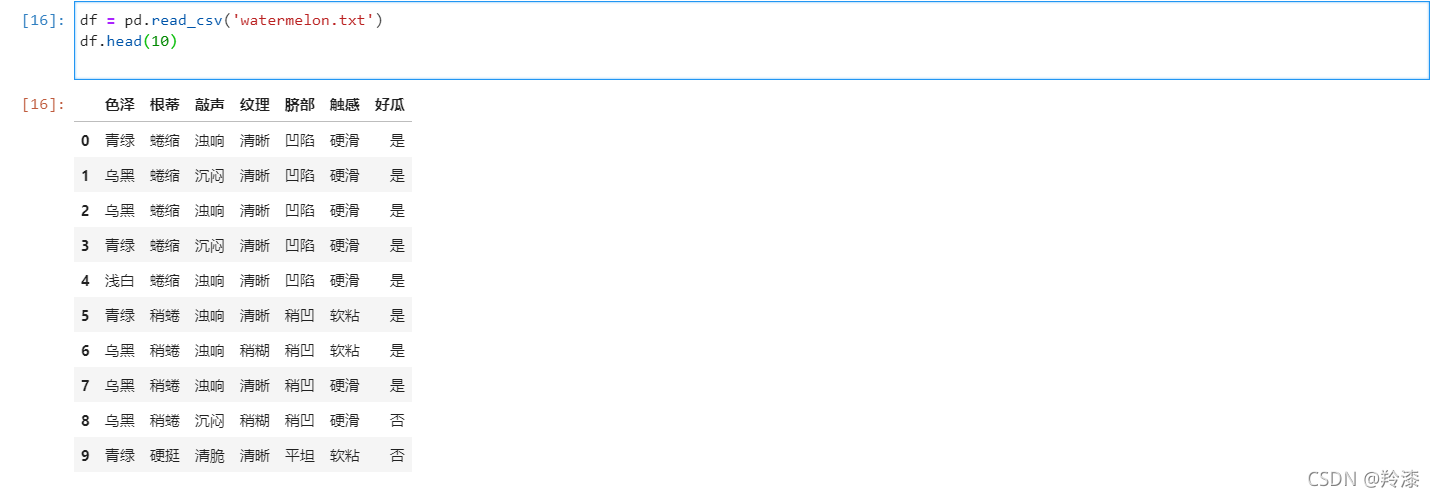
  • 读取文件，可以看到读出来的数据
df = pd.read_csv('watermelon.txt')
df.head(10)

在这里插入图片描述

  • 将特征值全部转化为数字
df['色泽']=df['色泽'].map({'浅白':1,'青绿':2,'乌黑':3})
df['根蒂']=df['根蒂'].map({'稍蜷':1,'蜷缩':2,'硬挺':3})
df['敲声']=df['敲声'].map({'清脆':1,'浊响':2,'沉闷':3})
df['纹理']=df['纹理'].map({'清晰':1,'稍糊':2,'模糊':3})
df['脐部']=df['脐部'].map({'平坦':1,'稍凹':2,'凹陷':3})
df['触感'] = np.where(df['触感']=="硬滑",1,2)
df['好瓜'] = np.where(df['好瓜']=="是",1,0)
x_train=df[['色泽','根蒂','敲声','纹理','脐部','触感']]
y_train=df['好瓜']
print(df)
id3=tree.DecisionTreeClassifier(criterion='entropy')
id3=id3.fit(x_train,y_train)
print(id3)

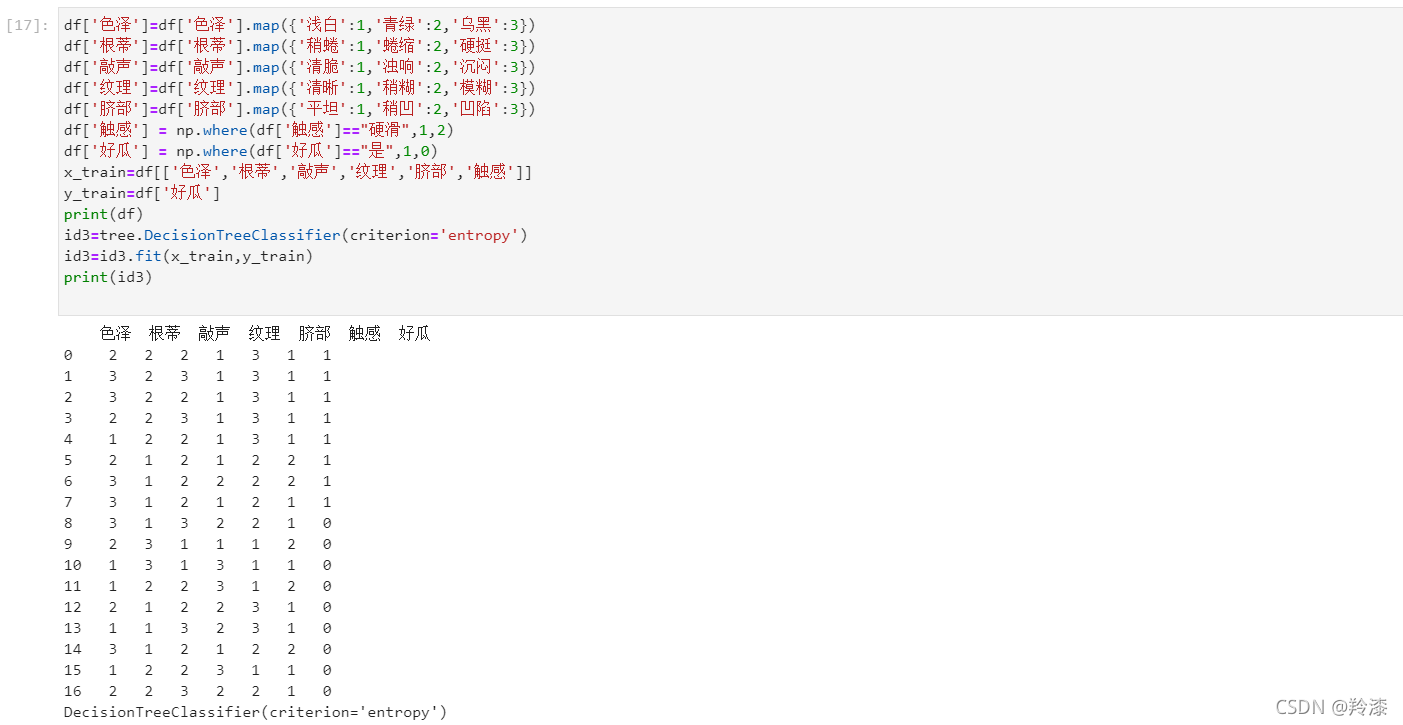
在这里插入图片描述

  • 训练并进行可视化，DecisionTreeClassifier的参数为entropy时是id3算法，默认是CART算法，没有C4.5算法
id3=tree.DecisionTreeClassifier(criterion='entropy')
id3=id3.fit(x_train,y_train)
labels = ['色泽', '根蒂', '敲击', '纹理', '脐部', '触感']
dot_data = tree.export_graphviz(id3
,feature_names=labels
,class_names=["好瓜","坏瓜"]
,filled=True
,rounded=True
)
graph = graphviz.Source(dot_data)
graph

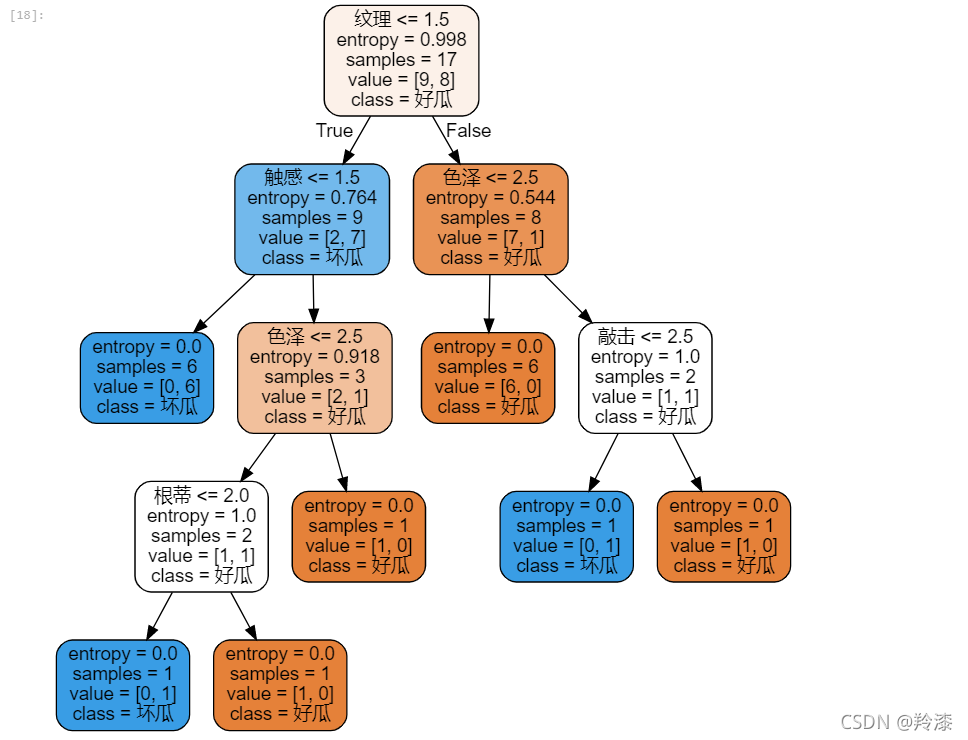
在这里插入图片描述

四、C4.5算法实现

  • C4.5算法介绍
    C4.5是决策树核心算法ID3的改进算法，所以步骤和ID3是一样的，只是把信息增益变为信息增益率了，就是算出来信息增益之后再除以该特征的信息熵。
  • 由于变得不多，只是把得到信息增益的那步再增加一步，得到信息增益率
## 实现C4.5算法
def chooseBestFeatureToSplit_4(dataSet, labels):"""选择最好的数据集划分特征，根据信息增益值来计算:param dataSet::return:"""# 得到数据的特征值总数numFeatures = len(dataSet[0]) - 1# 计算出基础信息熵baseEntropy = calcShannonEnt(dataSet)# 基础信息增益为0.0bestInfoGain = 0.0# 最好的特征值bestFeature = -1# 对每个特征值进行求信息熵for i in range(numFeatures):# 得到数据集中所有的当前特征值列表featList = [example[i] for example in dataSet]# 将当前特征唯一化，也就是说当前特征值中共有多少种uniqueVals = set(featList)# 新的熵，代表当前特征值的熵newEntropy = 0.0# 遍历现在有的特征的可能性for value in uniqueVals:# 在全部数据集的当前特征位置上，找到该特征值等于当前值的集合subDataSet = splitDataSet(dataSet=dataSet, axis=i, value=value)# 计算出权重prob = len(subDataSet) / float(len(dataSet))# 计算出当前特征值的熵newEntropy += prob * calcShannonEnt(subDataSet)# 计算出“信息增益”infoGain = baseEntropy - newEntropyinfoGain = infoGain/newEntropy#print('当前特征值为：' + labels[i] + '，对应的信息增益值为：' + str(infoGain)+"i等于"+str(i))#如果当前的信息增益比原来的大if infoGain > bestInfoGain:# 最好的信息增益bestInfoGain = infoGain# 新的最好的用来划分的特征值bestFeature = i#print('信息增益最大的特征为：' + labels[bestFeature])return bestFeature
  • 创建树的函数还是改了一下，免得混淆
def createTree_4(dataSet, labels):"""创建决策树:param dataSet: 数据集:param labels: 特征标签:return:"""# 拿到所有数据集的分类标签classList = [example[-1] for example in dataSet]# 统计第一个标签出现的次数，与总标签个数比较，如果相等则说明当前列表中全部都是一种标签，此时停止划分if classList.count(classList[0]) == len(classList):return classList[0]# 计算第一行有多少个数据，如果只有一个的话说明所有的特征属性都遍历完了，剩下的一个就是类别标签，或者所有的样本在全部属性上都一致if len(dataSet[0]) == 1 or judgeEqualLabels(dataSet):# 返回剩下标签中出现次数较多的那个return majorityCnt(classList)# 选择最好的划分特征，得到该特征的下标bestFeat = chooseBestFeatureToSplit_4(dataSet=dataSet, labels=labels)print(bestFeat)# 得到最好特征的名称bestFeatLabel = labels[bestFeat]print(bestFeatLabel)# 使用一个字典来存储树结构，分叉处为划分的特征名称myTree = {bestFeatLabel: {}}# 将本次划分的特征值从列表中删除掉del(labels[bestFeat])# 得到当前特征标签的所有可能值featValues = [example[bestFeat] for example in dataSet]# 唯一化，去掉重复的特征值uniqueVals = set(featValues)# 遍历所有的特征值for value in uniqueVals:# 得到剩下的特征标签subLabels = labels[:]subTree = createTree(splitDataSet(dataSet=dataSet, axis=bestFeat, value=value), subLabels)# 递归调用，将数据集中该特征等于当前特征值的所有数据划分到当前节点下，递归调用时需要先将当前的特征去除掉myTree[bestFeatLabel][value] = subTreereturn myTree
  • 调用函数，看一下字典型的树
mytree_4=createTree_4(data,labels)
print(mytree_4)

在这里插入图片描述

  • 然后补全之后再可视化
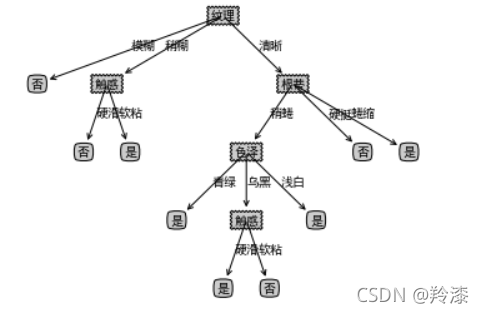
makeTreeFull(mytree_4,labels_full,default='未知')
createPlot(mytree_4)

在这里插入图片描述

五、CART算法实现

  • CART介绍
    CART算法是一种二分递归分割技术，把当前样本划分为两个子样本，使得生成的每个非叶子结点都有两个分支，因此CART算法生成的决策树是结构简洁的二叉树。由于CART算法构成的是一个二叉树，它在每一步的决策时只能是“是”或者“否”，即使一个feature有多个取值，也是把数据分为两部分。
  • 使用sklearn库实现，导入包
import pandas as pd
from sklearn import tree
import graphviz
  • 导入数据并读取
df = pd.read_csv('watermelon.txt')
df.head(10)
  • 将特征值化为数字
df['色泽']=df['色泽'].map({'浅白':1,'青绿':2,'乌黑':3})
df['根蒂']=df['根蒂'].map({'稍蜷':1,'蜷缩':2,'硬挺':3})
df['敲声']=df['敲声'].map({'清脆':1,'浊响':2,'沉闷':3})
df['纹理']=df['纹理'].map({'清晰':1,'稍糊':2,'模糊':3})
df['脐部']=df['脐部'].map({'平坦':1,'稍凹':2,'凹陷':3})
df['触感'] = np.where(df['触感']=="硬滑",1,2)
df['好瓜'] = np.where(df['好瓜']=="是",1,0)
x_train=df[['色泽','根蒂','敲声','纹理','脐部','触感']]
y_train=df['好瓜']
  • 训练得到树，并且可视化
# 构建模型并训练
labels = ['色泽', '根蒂', '敲击', '纹理', '脐部', '触感']
gini=tree.DecisionTreeClassifier()
gini=gini.fit(x_train,y_train)
#实现决策树的可视化
gini_data = tree.export_graphviz(gini
,feature_names=labels
,class_names=["好瓜","坏瓜"]
,filled=True
,rounded=True
)
gini_graph = graphviz.Source(gini_data)
gini_graph

在这里插入图片描述

六、总结

决策树理解还是不难的，就是要清楚每种算法的划分依据，步骤大致是先计算评判标准，后面再根据评判结果排序，最后根据顺序来递归建树。

参考文献

机器学习笔记（4）——ID3决策树算法及其Python实现
挑选西瓜（决策树实现）


http://chatgpt.dhexx.cn/article/N5D8OSSh.shtml

相关文章

机器学习算法:决策树算法

机器学习算法:决策树算法

1.基本定义 决策树(Decision Tree)是一种基本的分类和回归算法。该算法模型呈树形结构&#xff0c;主要由结点和有向边组成。结点又分为两种类型&#xff1a;内部结点和叶子结点。内部结点表示在一个属性或特征上的测试&#xff0c;每一个结点分枝代表一个测试输出&#xff0c;…
阅读更多...
决策树算法应用及结果解读

决策树算法应用及结果解读

作者&#xff1a;林骥 来源&#xff1a;林骥 引言 本文是我写的人工智能系列的第 8 篇文章&#xff0c;文末有前面 7 篇文章的链接&#xff0c;推荐你阅读、分享和交流。 1. 决策树算法简介 决策树是一种应用非常广泛的算法&#xff0c;比如语音识别、人脸识别、医疗诊断、模式…
阅读更多...
机器学习算法（3）之决策树算法

机器学习算法（3）之决策树算法

前言&#xff1a;首先&#xff0c;在了解树模型之前&#xff0c;自然想到树模型和线性模型有什么区别呢&#xff1f;其中最重要的是&#xff0c;树形模型是一个一个特征进行处理&#xff0c;之前线性模型是所有特征给予权重相加得到一个新的值。决策树与逻辑回归的分类区别也在…
阅读更多...
机器学习基础 决策树算法

机器学习基础 决策树算法

文章目录 一、决策树算法简介二、决策树分类原理1. 熵1.1 概念1.2 案例 2. 决策树的划分依据一----信息增益2.1 概念2.2 案例 3. 决策树的划分依据二----信息增益率3.1 概念3.2 案例3.2.1 案例一3.2.2 案例二 3.3 为什么使用C4.5要好 4. 决策树的划分依据三 ----基尼值和基尼指…
阅读更多...
【机器学习常见算法】决策树算法(含示例代码)

【机器学习常见算法】决策树算法(含示例代码)

决策树(Decision Tree)是一种非参数的有监督学习方法&#xff0c;它能够从一系列有特征和标签的数据中总结出决策规 则&#xff0c;并用树状图的结构来呈现这些规则&#xff0c;以解决分类和回归问题。决策树算法容易理解&#xff0c;适用各种数据&#xff0c;在解决各 种问题时…
阅读更多...
【决策树】深入浅出讲解决策树算法（原理、构建）

【决策树】深入浅出讲解决策树算法（原理、构建）

本文收录于《深入浅出讲解自然语言处理》专栏&#xff0c;此专栏聚焦于自然语言处理领域的各大经典算法&#xff0c;将持续更新&#xff0c;欢迎大家订阅&#xff01;​个人主页&#xff1a;有梦想的程序星空​个人介绍&#xff1a;小编是人工智能领域硕士&#xff0c;全栈工程…
阅读更多...
协方差矩阵推导

协方差矩阵推导

协方差定义&#xff1a;&#xff0c;其中分别为向量的均值。 设已知矩阵 则 样本自由度m-1&#xff0c;设&#xff0c;&#xff0c;则
阅读更多...
协方差矩阵到底有什么用？

协方差矩阵到底有什么用？

我们知道&#xff0c;线性代数&#xff0c;可以完成空间上的线性变换——旋转&#xff0c;缩放。对于协方差&#xff0c;我们隐约可以想到&#xff0c;它能解释一个随机变量&#xff0c;它在各个维度的变化程度。但是&#xff0c;这种认识其实还是处于比较浅层次的。数学嘛&…
阅读更多...
22协方差矩阵 matlab,协方差协方差矩阵【matlab实例】

22协方差矩阵 matlab,协方差协方差矩阵【matlab实例】

[今天看论文的时候又看到了协方差矩阵这个破东西，以前看模式分类的时候就特困扰，没想到现在还是搞不清楚，索性开始查协方差矩阵的资料，恶补之后决定马上记录下来，嘿嘿~ 协方差矩阵 协方差也只能处理二维问题，那维数多了自然就需要计算多个协方差，比如n维的数据集就需要计…
阅读更多...
透彻理解协方差矩阵

透彻理解协方差矩阵

2018-12-30 11:27:05 协方差及协方差矩阵有着特别广泛的应用&#xff0c;在多元高斯分布、高斯过程、卡尔曼滤波等算法中多有用到&#xff0c;本文从协方差、协方差矩阵讲起&#xff0c;并重点讲解协方差矩阵在高斯分布中的用法及意义&#xff0c;也是讲解高斯过程、贝叶斯优化…
阅读更多...
使用matlab编写协方差矩阵计算矩阵

使用matlab编写协方差矩阵计算矩阵

Dr.Can在他的教学视频&#xff08;【卡尔曼滤波器】2_数学基础_数据融合_协方差矩阵_状态空间方程_观测器问题&#xff09;中使用了足球运动员的数据介绍了协方差矩阵的概念和计算方法&#xff0c;原始数据如下图&#xff0c;那么协方差矩阵到底是什么&#xff1f;他有什么用&a…
阅读更多...
PCA与协方差矩阵

PCA与协方差矩阵

一、协方差矩阵 一个维度上方差的定义&#xff1a; 协方差的定义&#xff1a; &#xff08;a&#xff09; 协方差就是计算了两个维度之间的相关性&#xff0c;即这个样本的这两个维度之间有没有关系。 协方差为0&#xff0c;证明这两个维度之间没有关系&#xff0c;协方差为正&…
阅读更多...
浅谈协方差矩阵2

浅谈协方差矩阵2

在之前的博客中介绍过一次协方差矩阵&#xff1a; 浅谈协方差矩阵_Yunlong_Luo的博客-CSDN博客 这次希望在之前的基础上&#xff0c;把协方差矩阵介绍的更清楚一些&#xff0c;本文的很多素材来自于&#xff1a; A geometric interpretation of the covariance matrix 期望和…
阅读更多...
浅析协方差矩阵

浅析协方差矩阵

统计学的基本概念 概率论里面有几个基本的概念&#xff0c;分别是&#xff1a;样本的均值、方差、标准差。首先&#xff0c;我们给定一个含有n个样本的集合&#xff0c;下面给出这些概念的公式描述&#xff1a; 均值&#xff1a; 标准差&#xff1a; 方差&#xff1a; 均值描述…
阅读更多...
协方差矩阵用途

协方差矩阵用途

协方差两个用途&#xff1a; 各有缺陷 第二个用途&#xff1a;马氏距离&#xff08;曼哈顿距离&#xff09; 例如 欧式距离定义 马氏距离&#xff1a; 马氏距离意义&#xff1a; 案例&#xff1a; 鸢尾花案例 随机向量的变换 实际案例&#xff1a; 随机变量的线性组合
阅读更多...
协方差矩阵-Covariance Matrix

协方差矩阵-Covariance Matrix

首先我们要明白&#xff0c;协方差实际是在概率论和统计学中用于衡量两个变量的总体误差,当然方差是协方差的一种特殊情况&#xff0c;即当两个变量是相同情况。它表示的是两个变量的总体的误差&#xff0c;这与只表示一个变量误差的方差不同。如果两个变量的变化趋势一致&…
阅读更多...
协方差矩阵（Covariance Matrix）

协方差矩阵（Covariance Matrix）

群体均值和协方差矩阵定义 &#xff08;Population Mean and Covariance Matrix&#xff09; 1、学术定义 2、常规定义 协方差矩阵中每个元素的求法 用中文来描述&#xff0c;就是&#xff1a; 协方差(i,j)&#xff08;第i列的所有元素-第i列的均值&#xff09;*&#xff…
阅读更多...
超全面的协方差矩阵介绍

超全面的协方差矩阵介绍

阅读本文需要具备一定的线性代数基础&#xff0c;通过本文&#xff0c;你将对协方差矩阵有全面的理解。 定义 一组随机变量&#xff0c;共n个&#xff1a; X ( X 1 , X 2 , . . . , X n ) T \mathbf{X}(X_1,X_2,...,X_n)^T X(X1​,X2​,...,Xn​)T 两个随机变量的协方差&am…
阅读更多...
统计篇（四）-- 协方差矩阵的理解

统计篇（四）-- 协方差矩阵的理解

本文将针对协方差矩阵做一个详细的介绍&#xff0c;其中包括协方差矩阵的定义、数学背景与意义、计算公式的推导、几何解释&#xff0c;主要整理自下面两篇博客&#xff1a; peghoty-关于协方差矩阵的理解&#xff1a;http://blog.csdn.net/itplus/article/details/11452743协…
阅读更多...
欧拉函数的两种求法

欧拉函数的两种求法

引入&#xff1a;互质的概念&#xff1a;如果 正整数 a 与b 之间只有一个公约数1 则称a与 b 互为质数。 欧拉函数的定义&#xff1a; 1-N 中 与N 互质的数的个数 记作 Phi&#xff08;N&#xff09; 在算数基本定理中任意自然数能进行质因数拆分&#xff0c;那么由容斥原理&a…
阅读更多...
推荐文章

Copyright @ 2022~2023