二叉树是一种常见的数据结构，理解二叉树对于理解AVL树、红黑树都有重要意义，索性再重新梳理一下思路，加深印象。本文重点介绍二叉查找树。

1.二叉树与二叉查找树

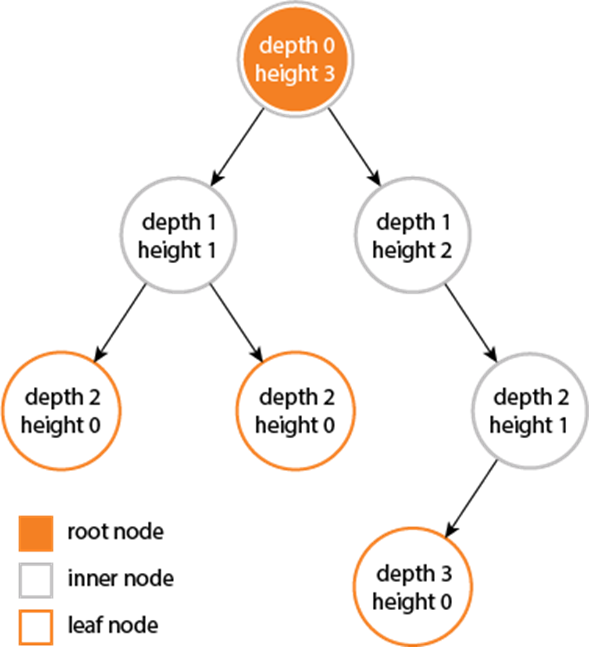
二叉树（binary tree）是树的一种特殊形式，这种树的每个节点做多只有两个孩子节点，二叉树结构如图：

二叉树的树形结构使它很适合扮演索引的角色，因此出现了一种特殊的二叉树—二叉查找树（binary search tree），二叉查找树在二叉树的基础上，又增加了几个条件：
1)如果左子树不为空，则左子树上所有的节点值均小于根节点值；
2）如果右子树不为空，则右子树上所有节点的值均大于根节点的值；
3）左右子树也都是二叉查找树
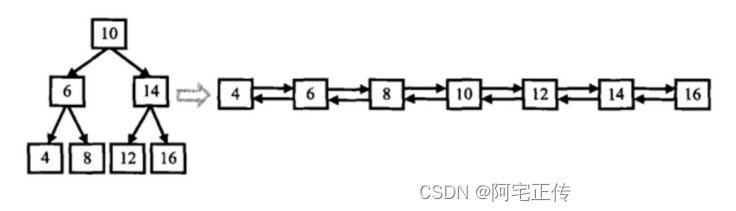
下图就是一个典型的二叉查找树:

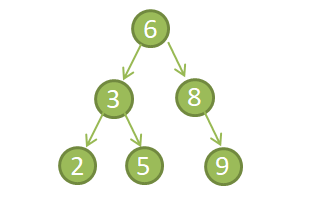
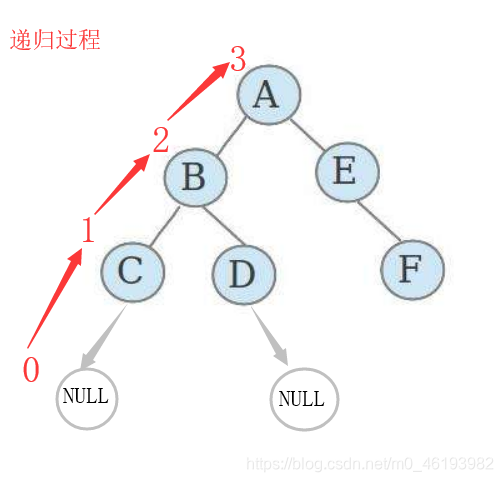
2.二叉树的深度优先遍历

2.1前序遍历

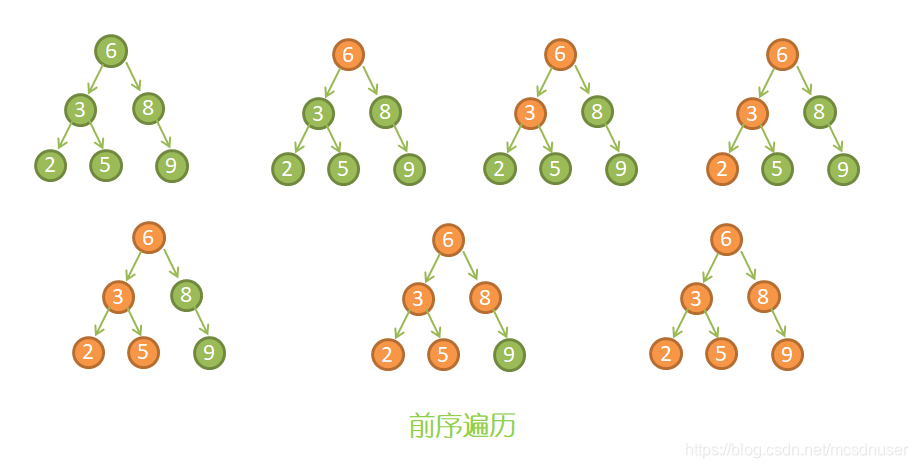
二叉树的前序遍历，输出顺序是根节点、左子树、右子树。示意图如图所示：
1）首先输出根节点6；
2）由于根节点6存在左子节点，输出左子节点3；
3）由于节点3也存在子节点，输出左子节点2；
4）节点2没有左子节点，也没右子节点，回到节点3，输出节点3右子节点5；
5）节点5既没左子节点，也没右子节点，回到节点6，输出节点6的右子节点8；
6）节点8没有左子节点，有右子节点，因此输出节点8的右子节点9；
到此为止，所有节点输出完毕。

2.2中序遍历

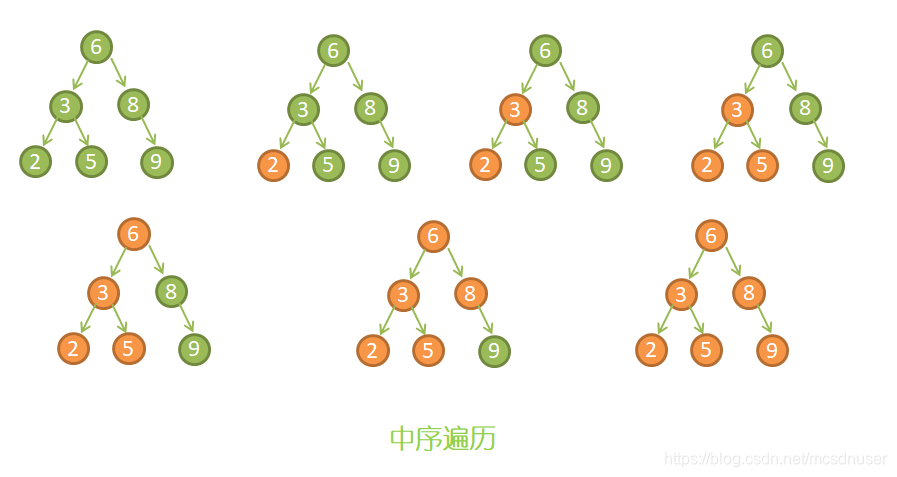
二叉树的前序遍历，输出顺序是左子树、根节点、右子树。示意图如图所示：
1）首先访问左子节点，如果左子节点还有左子节点，则继续深入访问，一直找到不再有左子节点的节点，输出节点2；
2）输出节点2的父节点节点3；
3）输出节点2的右节点节点5；
4）以节点2为根的左子树已输出完毕，这时输出整个二叉树的根节点节点6；
5）由于节点8没左子节点，直接输出节点8；
6）最后输出节点8的右子树节点9；
到此为止，所有节点输出完毕。

2.3后序遍历

二叉树的前序遍历，输出顺序是左子树、右子树、根节点。示意图如图所示：
1）首先访问左子节点，如果左子节点还有左子节点，则继续深入访问，一直找到不再有左子节点的节点，输出节点2；
2）输出节点2的右节点节点5；
3）输出节点2的父节点节点3；
4）以节点2为根的左子树已输出完毕，开始查找根节点的右子树，节点8没有左子节点，但有右子节点，输出右子节点9；
5）输出右子节点的父节点节点8；
6）最后输出节根节点节点6；
到此为止，所有节点输出完毕。

3.配套代码

三种遍历方式，用递归实现会非常简单。

/*** 二叉查找树*/
public class BinarySearchTree {//根节点TreeNode root;/*** 构建二叉查找树* @param node* @param data*/public void createTree(TreeNode node, int data){if(root == null){root = new TreeNode(data);}else{if(data < node.data){if(node.left == null){node.left = new TreeNode(data);}else{createTree(node.left,data);}}else{if(node.right == null){node.right = new TreeNode(data);}else{createTree(node.right,data);}}}}/***二叉树前序遍历* @param node*/public void preOrderTraversal(TreeNode node){if(node == null){return ;}System.out.println(node.data);preOrderTraversal(node.left);preOrderTraversal(node.right);}/***二叉树中序遍历* @param node*/public void middleOrderTraversal(TreeNode node){if(node == null){return ;}middleOrderTraversal(node.left);System.out.println(node.data);middleOrderTraversal(node.right);}/***二叉树后序遍历* @param node*/public void postOrderTraversal(TreeNode node){if(node == null){return ;}postOrderTraversal(node.left);postOrderTraversal(node.right);System.out.println(node.data);}
}
/*** 二叉树节点*/
class TreeNode {//节点数据int data;//左子树TreeNode1 left;//右子树TreeNode1 right;public TreeNode(int data) {this.data = data;}
}

测试类：

public  static void main(String[] args){int[] arr = {10,2,3,1,11};BinarySearchTree tree = new BinarySearchTree();for(int data : arr){tree.createTree(tree.root,data);}//前序遍历System.out.println("********前序遍历********");tree.preOrderTraversal(tree.root);//中序遍历System.out.println("********中序遍历********");tree.middleOrderTraversal(tree.root);//后序遍历System.out.println("********后序遍历********");tree.postOrderTraversal(tree.root);}