一、深度优先遍历

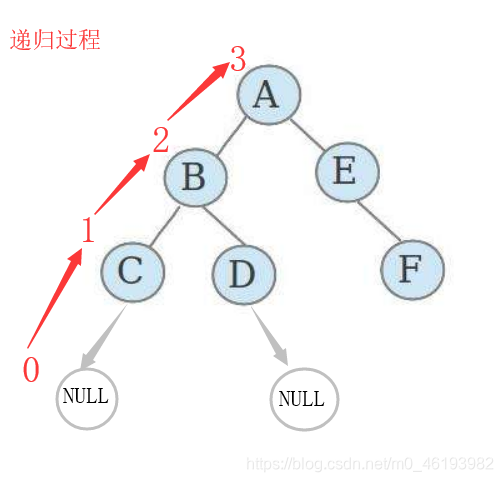
对每一个可能的分支路径深入到不能再深入为止，而且每个结点只能访问一次。
要特别注意的是，二叉树的深度优先遍历比较特殊，可以细分为先序遍历、中序遍历、后序遍历。具体说明如下：
先序遍历：对任一子树，先访问根，然后遍历其左子树，最后遍历其右子树。即：根、左、右
中序遍历：对任一子树，先遍历其左子树，然后访问根，最后遍历其右子树。即：左、根、右
后序遍历：对任一子树，先遍历其左子树，然后遍历其右子树，最后访问根。即：左、右、根
注：二叉树的具体构建详见此篇文章

二、先序遍历

1.算法思路

先序遍历就是在访问二叉树的结点的时候采用，先根，再左，再右的方式。

上图所示二叉树先序遍历即为：ABDGHCEIF
实现先序遍历思路非常简单，只需要巧妙的利用“递归”即可：

//树的先序遍历 Preorder traversal
void preorder(Node* node){if (node != NULL) {printf("%d ",node->data); // 根preorder(node->left); // 左子树preorder(node->right); // 右子树}
}

2.代码实现

// 先序遍历let preorderArr = [] // 存放遍历结果的数组function preorder(node) {if (node) {preorderArr.push(node.data);preorder(node.lChild);preorder(node.rChild);}}preorder(tree);console.log(preorderArr);

运行结果：

三、中序遍历

1.算法思路

中序遍历就是在访问二叉树的结点的时候采用，先左，再根，再右的方式。

上图所示二叉树中序遍历即为：GDHBAEICF
巧妙利用递归，与先序的代码只有一个顺序的区别：

//树的中序遍历 In-order traversal
void inorder(Node* node){if (node != NULL){inorder(node->left);printf("%d ",node->data);inorder(node->right);}
}

2.代码实现

// 中序遍历let inorderArr = []function inorder(node) {if (node) {inorder(node.lChild); // 左子树inorderArr.push(node.data); // 根inorder(node.rChild); // 右子树}}inorder(tree)console.log(inorderArr);

运行结果：

四、后序遍历

1.算法思路

后序遍历就是在访问二叉树的结点的时候采用，先左，再右，再根的方式。

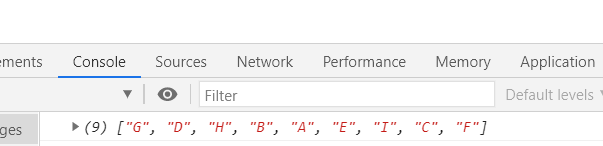
上图所示二叉树后序遍历即为：GHDBIEFCA
巧妙利用递归，与先序的代码只有一个顺序的区别：

//树的中序遍历 In-order traversal
void inorder(Node* node){if (node != NULL){inorder(node->left);inorder(node->right);printf("%d ",node->data);}
}

2.代码实现

// 后序遍历let postorderArr = []function postorder(node) {if (node) {postorder(node.lChild); // 左子树postorder(node.rChild); // 右子树postorderArr.push(node.data); // 根}}postorder(tree)console.log(postorderArr);

运行结果：