[算法步骤]

如果是空树，递归结束，深度为0；否则执行一下操作

• 递归计算左子树的深度计为m;
• 递归计算右子树的深度计为n;
• 如果m大于n，二叉树的深度为m+1，否则为n+1；

[算法描述]

int Depth(BiTree T)
{int m, n;if (T == NULL)return 0; //如果是空树，深度为0，递归结束else{m = Depth(T->lchild); //递归计算左子树的深度记为mn = Depth(T->rchild); //递归计算右子树的深度记为nif (m > n)return (m + 1); //二叉树的深度为m 与n的较大者加1elsereturn (n + 1);}
}

完整代码实现

//计算二叉树的深度
#include <iostream>
using namespace std;//二叉树的二叉链表存储表示
typedef struct BiNode
{char data;                      //结点数据域struct BiNode *lchild, *rchild; //左右孩子指针
} BiTNode, *BiTree;//建立二叉链表
void CreateBiTree(BiTree &T)
{//按先序次序输入二叉树中结点的值（一个字符），创建二叉链表表示的二叉树Tchar ch;cin >> ch;if (ch == '#')T = NULL; //递归结束，建空树else{T = new BiTNode;T->data = ch;            //生成根结点CreateBiTree(T->lchild); //递归创建左子树CreateBiTree(T->rchild); //递归创建右子树}                            //else
} //CreateBiTreeint Depth(BiTree T)
{int m, n;if (T == NULL)return 0; //如果是空树，深度为0，递归结束else{m = Depth(T->lchild); //递归计算左子树的深度记为mn = Depth(T->rchild); //递归计算右子树的深度记为nif (m > n)return (m + 1); //二叉树的深度为m 与n的较大者加1elsereturn (n + 1);}
}int main()
{BiTree tree;cout << "请输入建立二叉链表的序列：\n";CreateBiTree(tree);cout << "数的深度为：" << Depth(tree) << endl;
}

二叉树：

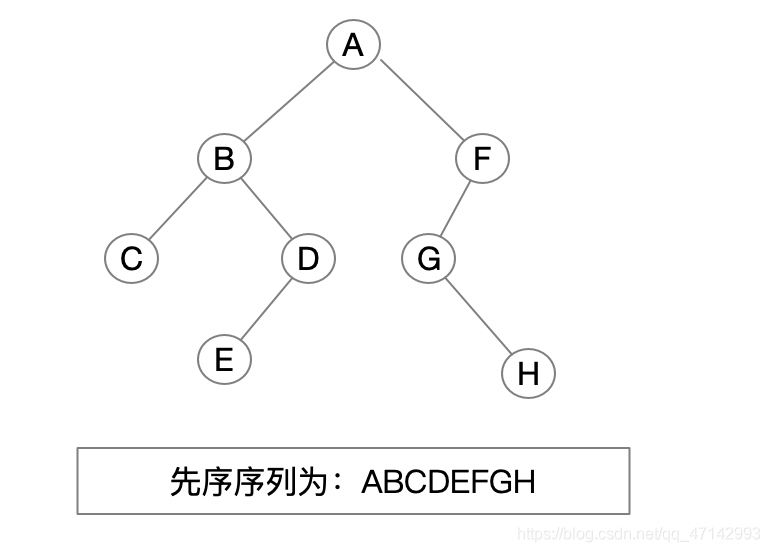
运行结果：