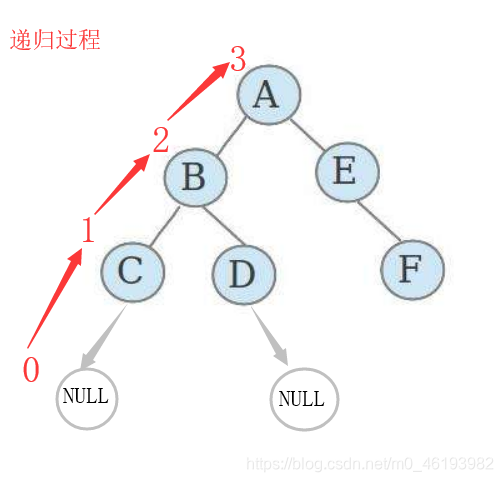
1.二叉树的max deep
1. 高度与深度
二叉树的高度: 任意一个节点到叶节点的max距离
深度: 任意一个节点到根节点的max距离
求深度: 后续 left right mid 先求子节点的深度,+1即为父节点深度
求高度 lef mid right +1 +1 +1逼近高度
2.求高度
1.递归思路
1+max(left,right)
递归函数 max f(root)
终止条件 if(root==null) return 0;
2.代码
// 法1 递归public int maxDepth(TreeNode root) {if (root==null) return 0;int maxleft=maxDepth(root.left);int maxright=maxDepth(root.right);return Math.max(maxleft,maxright)+1;}
3. 为什么深度=高度
二叉树根节点的高度与树的最大深度相等,高度叶到当前节点,深度当前节点到根,高度后续,深度前序
法二: 层序遍历
// 法二 层序遍历public int maxDepth02(TreeNode root) {if (root==null){return 0;}int dept=0;ArrayDeque<TreeNode> queue = new ArrayDeque<>();queue.offer(root);while (!queue.isEmpty()){int size=queue.size();// 一层元素的数量,来装下一层的元素for (int i = 0; i < size; i++) {TreeNode poll = queue.poll();if (poll.left!=null){queue.offer(poll.left);}if (poll.right!=null){queue.offer(poll.right);}}dept++;}return dept;}3. 法三: 直接求深度
前序 中左右+回溯
先求中间节点深度,left深度=right深度=中间+1,此时求右节点时需要回溯(我写的代码自带回溯,dept+1后不变了)
// 法3 直接求深度 前序 中左右int maxDept=0;public void maxDepth03(TreeNode root,int dept) {// dept是当前节点高度if (root==null){return ;}maxDept= maxDept>dept ? maxDept : dept;dept++;// 子节点高度maxDepth03(root.left,dept);maxDepth03(root.right,dept);}public int maxDepth03(TreeNode root) {maxDepth03(root,1);return maxDept;}
2. 二叉树最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
111.二叉树的最小深度1
返回它的最小深度 2
1. 法一 递归

public int minDepth(TreeNode root) {if (root==null){return 0;}int left = minDepth(root.left);int right = minDepth(root.right);if (root.left!=null&&root.right==null){return 1+left;}if (root.right!=null&&root.left==null){return 1+right;}return 1+Math.min(left,right);}法二 层序遍历
public int minDepth(TreeNode root) {if (root == null) {return 0;}int dept = 0;ArrayDeque<TreeNode> queue = new ArrayDeque<>();queue.offer(root);while (!queue.isEmpty()) {int size = queue.size();// 一层元素的数量,来装下一层的元素dept++;for (int i = 0; i < size; i++) {TreeNode poll = queue.poll();if (poll.left == null && poll.right == null) {return dept;}if (poll.left != null) {queue.offer(poll.left);}if (poll.right != null) {queue.offer(poll.right);}}}return dept;}
}
```
在这里插入代码片
`
## 3. 判断平衡二叉树
### 1. 衡二叉树,左右子树高度相差<=1
1. height f(node) // 返回节点高度,当不是平衡二叉树,返回-1
2. if(node==null) return 0;
3. 单层
left=f(left)
if(left==-1) return -1; 剪枝
right=f(right)
if(rght==-1){return -1}return abs(left-right)<=1 ? Max(left+right)+1;// 29. 平衡二叉树public boolean isBalanced(TreeNode root) {int balancedDG = isBalancedDG(root);return balancedDG==-1 ? false : true;}//public int isBalancedDG(TreeNode root) {if (root == null) {return 0;}int left = isBalancedDG(root.left);if (left==-1){ //剪枝return -1;}int right = isBalancedDG(root.right);if(right==-1){ // 防 左子树为0,右子树一串return -1; }return Math.abs(left-right)>1 ?-1 : Math.max(left,right)+1; }为什么right还要判断防