在帮助大家运维EDI平台的这几年中,常常有些客户反馈为什么之前发送的数据页面上都没有了呢?我想查询下之前的数据是否有成功发送给我们的客户应该怎么确认呢?业务数据量太大,文件占用磁盘空间太多,我如何快速地确认一些不需要的数据来清理释放磁盘空间呢?
回答上述问题,就需要给大家好好解释下知行之桥对文件存储的一个常常被大家忽略但是又非常重要的功能:文件归档。本文将介绍什么是文件归档功能以及如何使用它。
在了解知行之桥的文件归档功能前,首先您需要了解知行之桥对数据的处理逻辑,知行之桥将处理的所有数据以文件的形式存储在部署知行之桥应用程序的服务器上,这些数据通过工作流中的功能端口进行转换。知行之桥每个端口对数据的处理通过以下几个文件夹进行存储:
Send文件夹:存储该端口待发送的文件
Sent文件夹:存储该端口已成功处理的文件
Receive文件夹:存储该端口成功接收的文件
Logs文件夹:存储文件处理日志
Archive文件夹:存储归档的文件
同时,每个端口可以在高级设置页面设置是否对消息副本和Sent文件夹下的文件进行保留,如下图是AS2端口的设置页面:
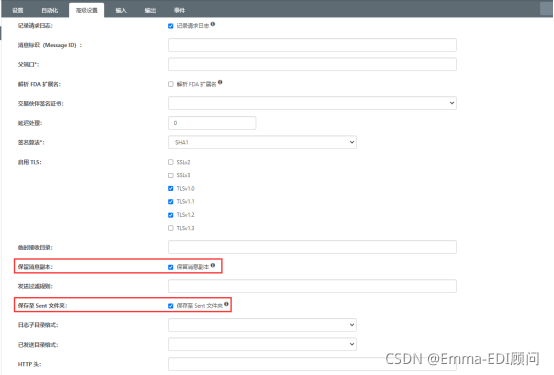
了解这些信息后,针对开头的几个问题,也就没有那么难懂了。
知行之桥每个端口处理数据时,都会将处理记录存入自带的Derby数据库,同时会显示在UI上,通过Web页面访问便可以查看数据的处理过程,但是当数据量达到一定程度后,比如百万条、千万条甚至更多时,通过Web页面登录知行之桥,UI页面显示加载时间过长,导致访问缓慢或者失败。同时,当数据量很大时,也会占用服务器更多的磁盘空间,当磁盘空间不足时,会导致知行之桥运行异常,从而影响业务数据的传输。
针对上述情况,知行之桥提供了文件归档功能,通过在个人设置→高级设置→清理选项中设置:
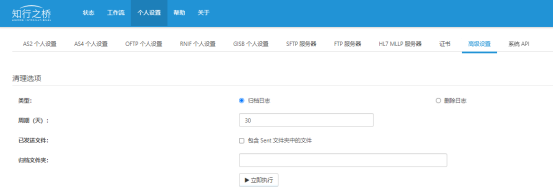
类型:勾选“归档日志”,启动归档功能。默认是归档日志。
周期(天):归档周期,即每次归档指定天数前的数据。默认是30天。
已发送文件:设置是否对每个端口下Sent文件夹下的文件进行归档。默认是不勾选的。
归档文件夹:自定义归档文件存储在服务器上的目录。默认将文件归档在每个端口下的Archive文件夹中。
注意:修改默认的配置后,点击“立即执行”按钮即生效。
那么归档文件是按照怎么样的逻辑存储的,如果在这里查看数据呢?
知行之桥在每天的凌晨00:00对文件执行归档操作的。
如果未设置归档文件夹,默认将文件归档在每个端口下的Archive文件夹中;如果设置了归档文件夹,将在设置的目录下按照“端口名称/Archive”自动创建归档文件夹。
Archive文件夹下将按照“执行日期/Logs/Sent/MessageID/文件”、“执行日期/Logs/Receive/MessageID/文件”归档每个端口的日志文件,如果勾选了“包含Sent文件夹的文件”,则还将自动创建“执行日期/Sent/文件”文件夹归档。
如下图使用的X12端口下的Archive文件夹对该端口的处理成功文件进行的归档:
端口名称:X12
归档设置:勾选“已发送文件”、归档文件夹设置为:E:\C-ArcESBCN\ArcESB(7867)\BackUp
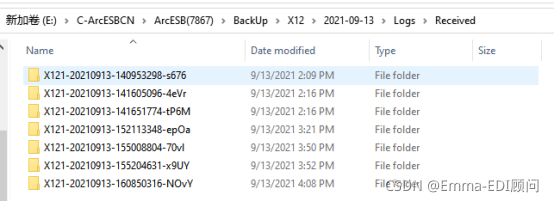
我们可以根据每个文件唯一的MessageID查看文件夹,每个文件夹下有对应的log文件和原始文件(一般是.eml形式存在,文件头部会带有一些Header信息,比如MessageID、文件名等)
最后,如何更好的使用归档功能呢?
实际使用知行之桥的归档功能,可以根据服务器磁盘大小、数据量合理设置归档周期,一般建议设置为180天(半年)。同时建议设置归档文件夹,这样在发生服务器磁盘空间不足,需要清理数据时,可以优先清理归档数据或者将其备份到其他服务器上,设置了归档文件夹将方便快捷的进行这些操作。