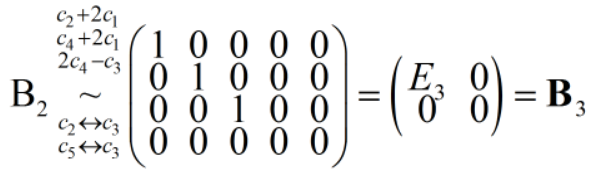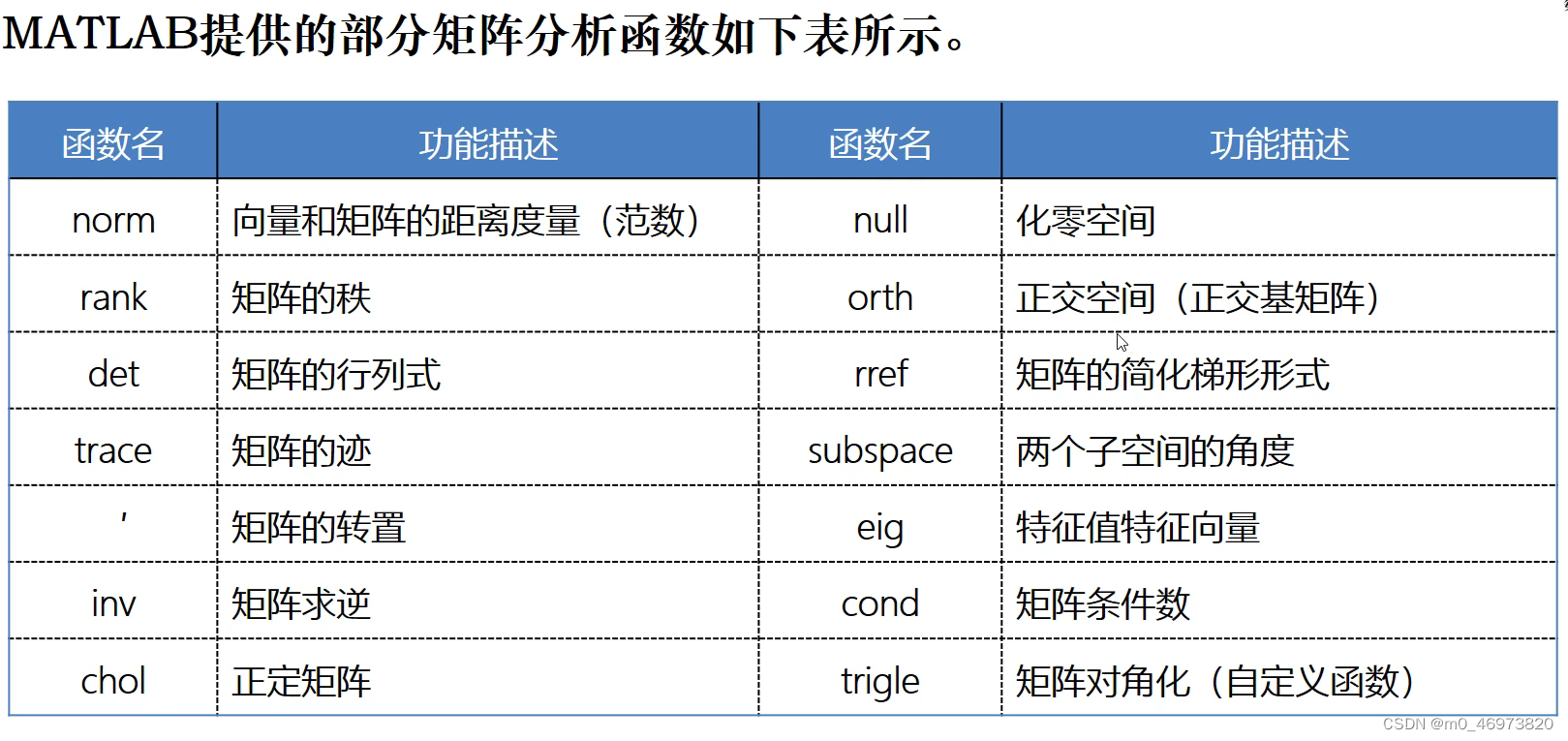
矩阵的逆
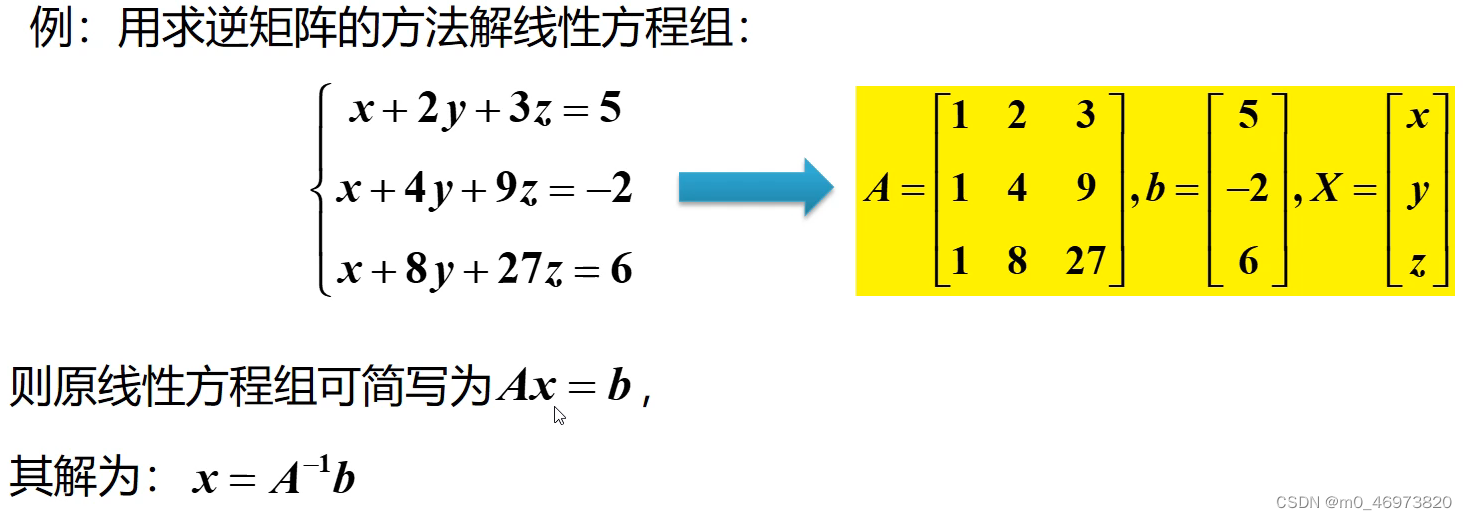
>> A*inv(A)
ans =
1.0000 0 -0.0000
-0.0000 1.0000 -0.0000
-0.0000 0 1.0000>> norm((ans-eye(3)))
ans =
1.8620e-15
一个矩阵中行(列)的最大线性无关组的行(列)向量的个数。线性变换后还能保持非零体积的最大维度。rank(A)
范数

>> A=randi([1,5],3,3);
>> n2=norm(A,2)n2 =
10.6827
>> sqrt(eig(A'*A))
ans =
0.5284
4.0744
10.6827
一范数,二范数,无穷范数
>> normA=[norm(A,1);norm(A);norm(A,inf)]
normA =
11.0000
10.6827
12.0000
矩阵A的条件数,矩阵A的范数与A的逆矩阵的范数的乘积。条件数越接近于1,矩阵性能越好。(矩阵的病态程度) cond(A,1)对应1范数。
矩阵的迹是矩阵对角线的元素的和,trace(A)。也是矩阵的特征值之和。
迹、特征值、行列式都是相似不变量。与坐标基变换无关。

>> A=round(5*randn(5))
>> [V,D]=eig(A)
测试矩阵 - MATLAB gallery - MathWorks 中国
矩阵的特征值与特征向量 与特征多项式
>> A=[3 1 5;6 1 2;9 2 1]
A =
3 1 5
6 1 2
9 2 1>> p=poly(A)
p =
1.0000 -5.0000 -48.0000 -18.0000
>> y=poly2sym(p)
y =
x^3 - 5*x^2 - 48*x - 18
>> r=roots(p)r =
9.9868
-4.5945
-0.3923>> [V,D]=eig(A)
V =
-0.5470 -0.5506 0.2087
-0.5125 0.3140 -0.9765
-0.6619 0.7735 0.0537
D =9.9868 0 0
0 -4.5945 0
0 0 -0.3923
矩阵初等变换及二次型
1、求行阶梯矩阵 及向量的基
>> A=[1 -1 -1 1 0;0 1 2 -4 1;2 -2 -4 6 -1;3 -3 -5 7 -1]
A =
1 -1 -1 1 0
0 1 2 -4 1
2 -2 -4 6 -1
3 -3 -5 7 -1>> [R,jb]=rref(A)
R = 行阶梯
1.0000 0 0 -1.0000 0.5000
0 1.0000 0 0 0
0 0 1.0000 -2.0000 0.5000
0 0 0 0 0
jb =1 2 3
>> r=length(jb) 相当于A的秩
r =
3
>> A(:,jb)
ans = 极大线性无关组
1 -1 -1
0 1 2
2 -2 -4
3 -3 -5

>> a1=[1;-2;2;3];a2=[-2;4;-1;3];a3=[-1;2;0;3];a4=[0;6;2;3];a5=[2;-6;3;4];
>> a1a1 =
1
-2
2
3>> A=[a1,a2,a3,a4,a5]
A =
1 -2 -1 0 2
-2 4 2 6 -6
2 -1 0 2 3
3 3 3 3 4>> [R,jb]=rref(A)
R =
1.0000 0 0.3333 0 1.7778
0 1.0000 0.6667 0 -0.1111
0 0 0 1.0000 -0.3333
0 0 0 0 0
jb =1 2 4
>> A(:,jb)
ans =
1 -2 0
-2 4 6
2 -1 2
3 3 3
2、正交基,正交矩阵orth()
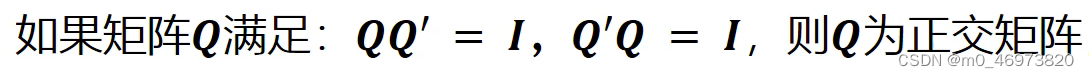

>> Q=orth(A) A的正交矩阵
>> A=round(3*randn(3,3));
>> q=orth(A);
>> norm(eye(rank(A)) - q'*q ,'fro')ans =
3.3891e-16
3、正定矩阵:在对称矩阵的基础上,如果一个对称矩阵所有的主子行列式均为正数,则称该矩阵为正定矩阵。p=0,为正定矩阵。
>> [D,p]=chol(A)
D =
1.0000 -1.0000 0
0 1.0000 1.0000
0 0 1.4142
p =0
4、矩阵对角化:nxn的矩阵对角化的条件是其具有n个线性无关的特征向量。存在一个可逆矩阵P使得P的逆*A*P是对角矩阵,则称A可对角化。
>> A=[11 -6 4 -10 -4;-3 5 -2 4 1;-8 12 -3 12 4;1 6 -2 3 -1;8 -18 8 -14 -1];
>> [V,D]=eig(A)V =
0.3244 -0.6922 0.0408 0.5536 0.0086
-0.1622 0.1831 0.1280 -0.2955 -0.1880
-0.6489 0.5493 0.3840 -0.5161 0.3588
-0.1622 -0.1428 0.4248 0.3330 0.5554
0.6489 -0.4065 -0.8088 0.4785 -0.7262
D = 特征值各不相同,一定可以对角化(5是二重根)3.0000 0 0 0 0
0 5.0000 0 0 0
0 0 5.0000 0 0
0 0 0 1.0000 0
0 0 0 0 1.0000>> rank(V)
ans =
5
求基础解系
>> A1=5*eye(rank(A)) -A
A1 =
-6 6 -4 10 4
3 0 2 -4 -1
8 -12 8 -12 -4
-1 -6 2 2 1
-8 18 -8 14 6>> x1=null(A1,'r') 零空间
x1 =
2.0000 1.0000
-0.3333 -0.3333
-1.0000 -1.0000
1.0000 0
0 1.0000>> inv(V)*A*V
ans =
3.0000 0.0000 0.0000 -0.0000 -0.0000
0.0000 5.0000 -0.0000 0.0000 -0.0000
0.0000 0.0000 5.0000 0.0000 -0.0000
0.0000 -0.0000 -0.0000 1.0000 0.0000
-0.0000 0.0000 0.0000 -0.0000 1.0000
实对称阵都可对角化,对角线元素为A的特征值 。

5、二次型化为标准型

>> A=[17 -2 -2;-2 14 -4;-2 -4 14];
>> [P,D]=eig(A);
>> syms y1 y2 y3
>> y=[y1;y2;y3];
>> X=vpa(P*y,3) 设置有效数字为3位
X = 正交变换X=Py
0.333*y1 - 0.298*y2 + 0.894*y3
0.667*y1 - 0.596*y2 - 0.447*y3
0.667*y1 + 0.745*y2
>> fn=[y1,y2,y3]*D*y 标准型
fn =
9*y1^2 + 18*y2^2 + 18*y3^2
问题注意