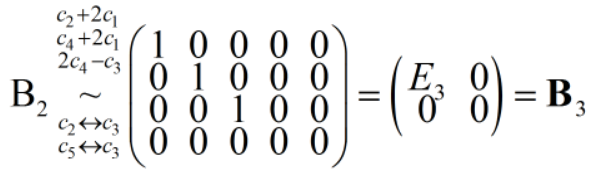(完整的程序附在文末)
1、问题描述:
用C/C++设计一个算法,把矩阵M化为行最简形梯形矩阵A。矩阵A应该满足以下几个条件:
1)若有零行,则零行应在最下方;
2)非零首元(即非零行的第一个不为零的元素)的列标号随行标号的增加而严格递增;
3)非零首元所在的列除了非零首元外,其余元素全为0;
4)非零首元都为1.
输入是一个文件input.txt
1)第一行会输入样本数k;
2)每个样本的第一行会输入n, m,表示矩阵M是nm维的;
3)接下来的n行里,每一行会输入m个元素,以空格隔开.
输出是一个文件output.txt
2)每个样本的第一行会输出n, m,表示最简形梯形矩阵A是nm维的;
3)接下来的n行里,每一行会输出m个元素,以空格隔开.
2、算法流程:
依据题目描述,我们要写出一个能够依次处理多组数据的、能把任意矩阵化为简化阶梯形形式的程序。考虑到矩阵化为简化阶梯形的过程较为繁琐,所以把化简过程分为将矩阵化为阶梯型、将阶梯型化为简化阶梯型两部分。
1)txt文件的读入和输出的实现

2)实现多组数据的处理
为了使程序能处理多组数据,要用到计数循环,即:
(1) 输入要处理的数据有多少组,在我的程序中记为k;
(2) 定义并赋值k1=1,这里的k1表示正在处理第几组数据;
(3) 每处理完一组数据后,使得k1增加1;
(4) k1=k时处理完最后一组数据,此时k1再加1,即k1>1,跳出循环.

3)矩阵的输入
考虑到矩阵包含行和列,是一个二次数列的集合,采用数组记录矩阵会比较方便。这里记为a[m][n].
(1)输入数组的总行数m和总列数n;
(2)定义i、j分别表示当前讨论的数是在数组的第i行、第j列(在我的程序中还
定义了i2、j2等参数,即在i、j已经有特定的意义,表示第i行第j列时,进而分析第i2行、第j2列的数。总之,i表示行,j表示列);
(3)使i=1,开始一个循环,每次循环结束后i增加1,i>m后跳出循环。在这个循
环中使j=1,开始另一个循环,每次循环结束后j增加1,j>n后跳出循环.
(4)在上述循环中,依次从键盘读取a[i][j].
这样,我们就做到了从上往下、从左往右依次输入数字,使得数字在数组中的位置与在矩阵中的位置完全相同。

以一个3x3,从上往下、从左至右数字依次递增的矩阵为例,我们得到的数组的各个存储格存储的数据如下图:


4)将一般矩阵化为阶梯型
要想化矩阵为阶梯型,必须从左至右找到每个主元列中的主元,再用主元消去主元正下方的数。首先需要找主元,我采用了类似将矩阵各数字输入数组的类似的方法:用两个循环语句实现:从左至右逐列分析,分析每列时自上而下依次分析每个数字。
(1) 换行
主元位置的数不能为零,所以分析某一列的时候,我们自上而下找第一个不为零的数,让这个数存在的一行与含有该列的主元位置的那一行交换,即换行,这样一来就保证了主元位置不为0。
那么问题来了。若第一列已经处理好,我们要进行第二列的操作时,我们要从第二个数开始自上而下进行判断某个数是否为零。因为若这一列存在主元位置,必然是该列的第二个数。主元位置上方的排序已经完成,不能再动了。那么第三列呢?有两种情况:(a)若第二列找到了主元,第三列有主元位置的话必定是该列第三个;(b)若第二行没有主元,第三列有主元位置的话必定是从上往下数第二个。而我们要从主元位置开始自上而下找非零值,也就是说前面的非主元列会对之后的分析造成影响。经深入思考,我发现当判断到第j列时,用v代表第j列之前有多少非主元列,若第j列有主元,必然是该列第(j-v)个。
但是,我们并不知道某一列是否是主元列,如果不是,这一列不需要进行行交换。如何判断呢?我们自上而下找非零元素,若全部的数均为零,则该列为非主元列,此时v++,并用break跳出循环。

换行比较简单,我利用了一个新的数组b来临时存储数据。

(2)利用主元消除该列下方其他行元素
这里我一开始打算将各个主元化为1后再把该列其他数化为0,但是考虑到含有主元的行可能会出现小数,导致之后的处理出现偏差,最终还是决定放大各个数而不是缩小。假设我要用含有某个主元的一行消除第i行,第i行每个数乘以该主元,含有主元的一行乘以主元列中第i行的元素,两行相减赋给第i行。为了避免含主元的一行数据过大,我们在操作结束后除以原来乘的那个数。(因为数据会改变,一开始用一个变量s2来存储这个数。)之后用break跳出循环。

至此,我们将矩阵化为了阶梯型。
5)将阶梯型化为简化阶梯型
我们从最后一行开始向上逐行分析,每一行从左至右第一个非零元素必为主元。

将主元化为1,把主元上方的数全部化为0.当然,如果上面的数为零则不处理。
在这里,因为数据处理后会变动,这里利用v记录信息。v等不等于-1是用来记录该数是否为零的一个标准。至此,数据处理全部完成。

6)矩阵的输出。和输入类似,逐行、逐列输出。(保留三位小数)

3、实验结果
将一个input.txt文件放在与程序相同的文件夹下,运行程序,输出output.txt。


在数学里,将一个简单的矩阵化为简化阶梯型很简单,我们的思路也相当明确。但是,当我们要为程序设计一个算法,让程序自己能够用特定的方式解决问题时,却觉得相当的复杂。主元的寻找,一眼就能看出来的,但要让程序做到,不得不绞尽脑汁想出那几行代码。所以,我们要学会探究解决问题的方法的本质。很多显然的事在深究后并不是那么的“显然”,但是一旦我们发现了其中的原理,思想的理解上和之后解决问题的能力上就会有很大的飞越。
完整程序如下:
#include<stdio.h>
int main(){int k,k1,m,n,i,j,i2,j2,i3,j3,v,s1,s2;float a[100][100],b[100][100];FILE *fpRead=fopen("input.txt","r");FILE *fpWrite=fopen("output.txt","w");if(fpRead== NULL){ return 0; } fscanf(fpRead,"%d",&k);for(k1=1;k1<=k;k1++){fscanf(fpRead,"%d %d",&m,&n);for(i=1;i<=m;i++){for(j=1;j<=n;j++)fscanf(fpRead,"%f",&a[i][j]);}v=0;for(j=1;j<=n;j++){for(i=j-v;i<=m;i++){if(i== m&&a[i][j]== 0){v++;break;}else if(a[i][j]= =0)continue;else{for(j2=1;j2<=n;j2++){b[i][j2]=a[i][j2];a[i][j2]=a[j-v][j2];a[j-v][j2]=b[i][j2];}s1=a[j-v][j];for(i2=j-v+1;i2<=m;i2++){s2=a[i2][j];for(j2=1;j2<=n;j2++){if(s2==0)break;else{a[i2][j2]*=s1;a[j-v][j2]*=s2;a[i2][j2]-=a[j-v][j2];a[j-v][j2]/=s2;}}}break;}}}for(i=m;i>=1;i--){for(j=1;j<=n;j++){if(a[i][j]== 0)continue;else{s1=a[i][j];for(j2=j;j2<=n;j2++)a[i][j2]/=s1;for(i2=i-1;i2>=1;i2--){if(a[i2][j]!=0){s1=a[i2][j];v=-1;}if(v!=-1)s1=0;for(j2=j;j2<=n;j2++)a[i2][j2]=a[i2][j2]-a[i][j2]*s1;}break;}}} if(fpWrite== NULL){ return 0; } if(k1== 1)fprintf(fpWrite,"%d\n",k);fprintf(fpWrite,"%d %d\n",m,n);for(i3=1;i3<=m;i3++){for(j3=1;j3<=n;j3++){if(a[i3][j3]==-0)a[i3][j3]=0;fprintf(fpWrite,"%.3f ",a[i3][j3]);}fprintf(fpWrite,"\n"); }}return 0;
}