首先这里我们先了解两个概念归档和压缩,归档就相当于将文件批量打包在一块,便于之后工作查找文件的位置,但是总体文件的大小是不变的,例如我们将10个不通路径下且每个大小都是10M的文件打包在一块,那么归档后的大小就是100M。而压缩的意思是,将文件归档在一块,并且利用某种技术将这个归档好的文件进行压缩,那么它总体的大小是有变化的,一般都是变小了。
1)那么我们一般对文件进行归档使用的命令是tar命令,下面我将列出该命令下各选项的作用:
- -c:创建新文档
- -x:释放备份文档
- -f:指定文档名称
- -z:处理".gz"格式
- -j:处理".bz2q"格式
- -J:处理".xz"格式
- -v:显示压缩或解压的过程
- -t:显示文档列表
- -p:保持原有权限
- -P:保持绝对路径
- -C:指定释放备份文件时的目标位置
- --exclude:排除的子目录
2)tar制作备份文件,可以通过“file 文件名”命令查看其压缩格式。
- tar -zvcf 备份文件名.tar.gz 被备份文档
- tar -jvcf 备份文件名.tar.bz2 被备份文档
- tar -Jvcf 备份文件名.tar.xz 被备份文档
那这些选项是怎么使用的呢,下面请看如下的例子:
例1:若要包当前目录下anaconda-ks.cfg和out.txt两个文件归档到new.tar文件里,命令如图1,其中选项“-f”后面记得带上归档文件的名称。可以使用“tar -t new.tar”查看归档列表包含什么文件,这里同样不要忘记在文件前添加选项“-f”。

图1
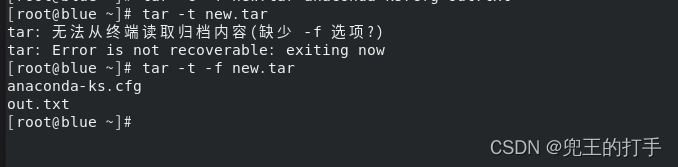
例2:结合例1,如果想看归档时备份了什么内容,可以加选项“-v”

例3:如果我们对一个目录下的文件做备份,记得加上选项“-P”,此选项的作用是保持绝对路径,那么我们在还原的时候,就不用指定原来的路径了,会自动帮助我们还原到原来的路径,当然你也可以用“-C”选项指定其他的目标位置。如图1,如果我们在备份的时候,没有加上“-P”选项,那么会把“/”删除,如图1,这里的选项是“-cvf”,可以看到会出现提示:从成员名中删除开头的“/”,这时候我们再输入“tar -tvf backup.tar”查看,如图2,红框处可以清晰看到已经不是绝对路径了。
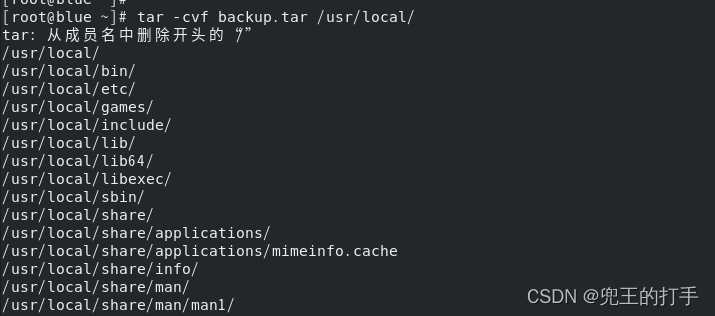
图1
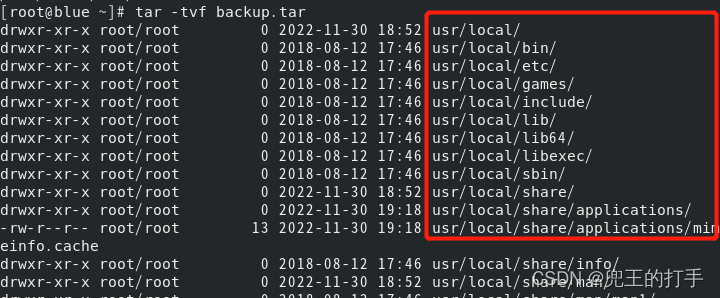
例4:结合例3,那么我们加上“-P”参数试一下,看会不会有原始路径的出现,这里我们输入“tar -cPvf backup2.tar /usr/local/ ”,如图1,然后再输入“tar -tvf backup2.loacl”,如图2,可以清晰看到对应的路径是原始路径。
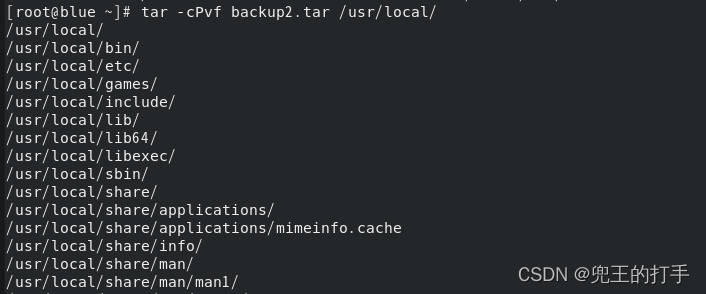
图1
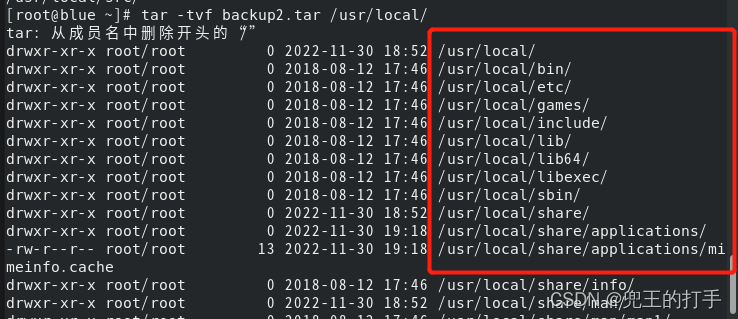
图2
例5:结合例1,我们看到将anaconda-ks.cfg和out.txt两个文件归档到new.tar文件里,其new.tar的大小变为10k,那么这个时候输入"gzip new.tar",可以看到所占容量变小了,但此时当前目录下存在的是“new.tar.gz”而不是“new.tar”

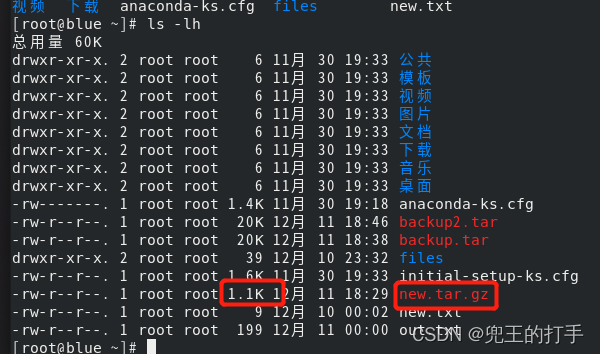
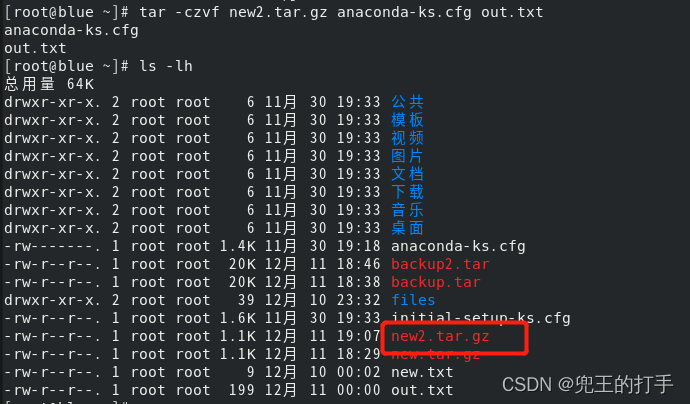
例6:如我们想把anaconda-ks.cfg和out.txt两个文件归档并压缩为new2.tar.gz,那要如何使用选项呢?如图所示:
例7:创建一个名为/root/backup,tar.bz2的tar文档,其应该包含/usr/local/的内容。次归档文件必须使用bz2进行压缩。