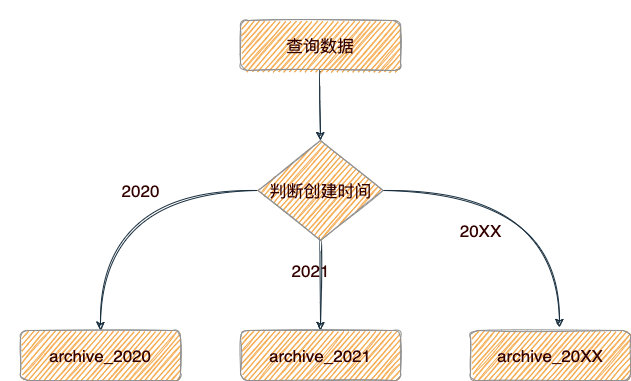
前言介绍

`
pt-archiver是用来归档表的工具，可以做到低影响、高性能的归档工具，从表中删除旧数据，而不会对 OLTP 查询产生太大影响。可以将数据插入到另一个表中，该表不需要在同一台服务器上。可以将其写入适合 LOAD DATA INFILE 的格式的文件中。或者两者都不做，只做一个增量删除。
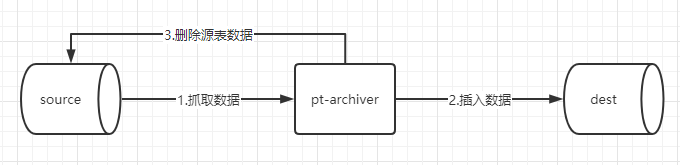
在这里插入图片描述
特点：

1.可以根据where条件获取需要清理的数据

2.支持事务批次提交，数据批次抓取

3.支持插入成功后，在删除的逻辑处理

4.支持文档备份

5.批量模式，自动匹配主键，支持重复归档

6.归档速度是存储过程脚本的6倍左右（本地测试）

7.支持归档不写binlog，杜绝无用数据占用空间问题以及报表解析问题

一、示例

一，条件归档，不删除源表数据，非批量插入方式

pt-archiver --source h=127.0.0.1,P=3306,u=root,p=091013,D=course-temp,t=t_course_info,A=utf8 --dest h=127.0.0.1,P=3306,u=root,p=091013,D=course-study,t=t_course_info,A=utf8 --charset=utf8 --where "f_course_time < 100000 " --progress=10000 --txn-size=5000 --limit=5000 --statistics --no-delete
在这里插入图片描述
二，条件归档，不删除源表数据，批量插入方式
pt-archiver --source h=127.0.0.1,P=3306,u=root,p=091013,D=course-temp,t=t_course_info,A=utf8 --dest h=127.0.0.1,P=3306,u=root,p=091013,D=course-study,t=t_course_info,A=utf8 --charset=utf8 --where "f_course_time < 100000 " --progress=5000 --txn-size=5000 --limit=1000 --statistics --no-delete --bulk-insert --ask-pass
在这里插入图片描述
三，条件归档，删除元源表数据，非批量插入，非批量删除
pt-archiver --source h=127.0.0.1,P=3306,u=root,p=091013,D=course-study,t=t_course_info,A=utf8 --dest h=127.0.0.1,P=3306,u=root,p=091013,D=course-temp,t=t_course_info,A=utf8 --charset=utf8 --where "f_course_time < 100000 " --progress=5000 --txn-size=5000 --limit=1000 --statistics --purge
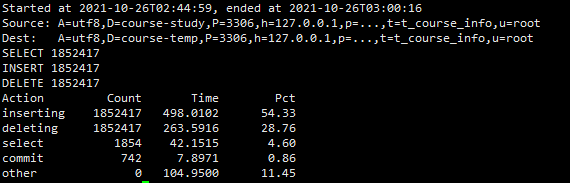
在这里插入图片描述
四，条件归档，删除元源表数据，批量插入，批量删除
pt-archiver --source h=127.0.0.1,P=3306,u=root,p=091013,D=course-temp,t=t_course_info,A=utf8 --dest h=127.0.0.1,P=3306,u=root,p=091013,D=course-study,t=t_course_info,A=utf8 --charset=utf8 --where "f_course_time < 100000 " --progress=5000 --txn-size=5000 --limit=1000 --bulk-insert --bulk-delete --statistics --purge
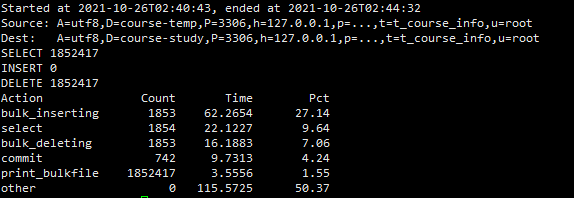
在这里插入图片描述
五，关联表条件归档
pt-archiver --source h=127.0.0.1,P=3306,u=root,p=091013,D=course-temp,t=t_course_info,A=utf8 --dest h=127.0.0.1,P=3306,u=root,p=091013,D=course-study,t=t_course_info,A=utf8 --charset=utf8 --where "f_course_time < 1000 and exists (select 1 from t_course_category where t_course_category.f_id= t_course_info.f_category_id and t_course_category.f_state = ‘1’ ) " --progress=5000 --txn-size=5000 --limit=1000 --statistics --no-delete --bulk-insert --ask-pass

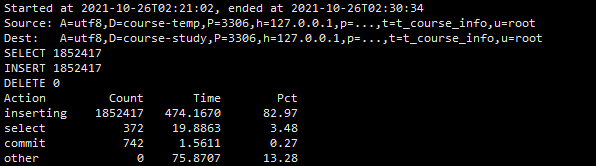
二、性能比较

在这里插入图片描述

三、备份到外部文件

导出到外部文件，不删除源表里的数据
pt-archiver --source h=127.0.0.1,D=course-study,t=t_course_info,u=root,p=123456 --where ‘1=1’ --no-check-charset --no-delete --file=“/tmp/source/archiver.dat”

四、安装

安装：
#先下载Percona Toolkit工具编译包
wget “https://www.percona.com/downloads/percona-toolkit/3.0.3/binary/tarball/percona-toolkit-3.0.3_x86_64.tar.gz”
#解压
tar xf percona-toolkit-3.0.3.tar.gz
#进入目录安装
cd percona-toolkit-3.0.3
#开始编译安装
yum install perl-ExtUtils-CBuilder perl-ExtUtils-MakeMaker
perl Makefile.PL
make
make install
#安装完了就有命令了
ll /usr/local/bin/pt-*
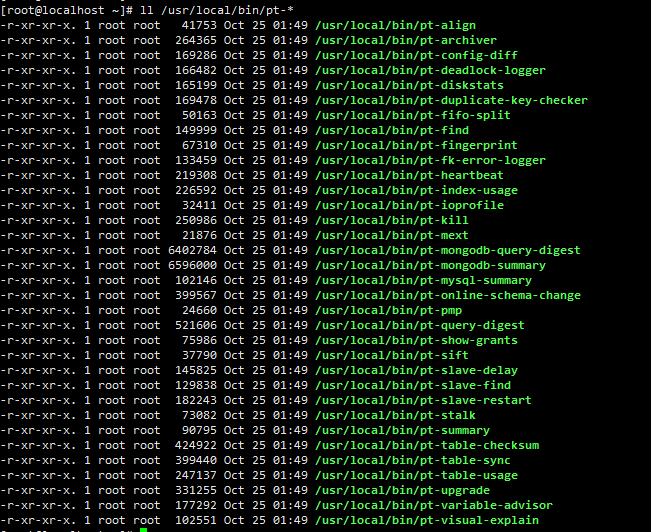
在这里插入图片描述

四、常用命令

在这里插入图片描述
-where ‘id<3000’ 设置操作条件
–limit 10000 每次取1000行数据给pt-archive处理
–txn-size 1000 设置1000行为一个事务提交一次
–progress 5000 每处理5000行输出一次处理信息
–statistics 结束的时候给出统计信息：开始的时间点，结束的时间点，查询的行数，归档的行数，删除的行数，以及各个阶段消耗的总的时间和比例，便于以此进行优化。只要不加上–quiet，默认情况下pt-archive都会输出执行过程的
–charset=UTF8 指定字符集为UTF8，字符集需要对应当前库的字符集来操作
–no-delete 表示不删除原来的数据，注意：如果不指定此参数，所有处理完成后，都会清理原表中的数据
–bulk-delete 批量删除source上的旧数据
–bulk-insert 批量插入数据到dest主机 (看dest的general log发现它是通过在dest主机上LOAD DATA LOCAL INFILE插入数据的)
–dry-run 模拟执行
–source 源数据
–dest 目标数据
–local：添加NO_WRITE_TO_BINLOG参数，OPTIMIZE 和 ANALYZE不写binlog
–analyze=ds 操作结束后，优化表空间（d表示dest，s表示source）