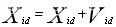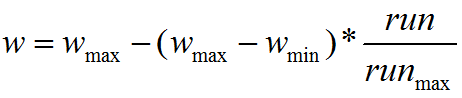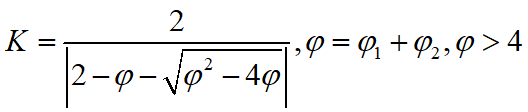文章目录
- 一、理论基础
- 二、案例背景
- 1、问题描述
- 2、解题思路及步骤
- 三、MATLAB程序实现
- 1、PSO算法参数设置
- 2、种群初始化
- 3、寻找初始极值
- 4、迭代寻优
- 5、结果分析
- 四、惯性权重
- 1、惯性权重的选择
- 2、 ω \omega ω变化的算法性能分析
- 五、参考文献
一、理论基础
粒子群算法(particle swarm optimization,PSO)是计算智能领域一种群体智能的优化算法。该算法最早由Kennedy和Eberhart在1995年提出的。PSO算法源于对鸟类捕食行为的研究,鸟类捕食时,找到食物最简单有效的策略就是搜寻当前距离食物最近的鸟的周围区域。PSO算法就是从这种生物种群行为特征中得到启发并用于求解优化问题的,算法中每个粒子都代表问题的一个潜在解,每个粒子对应一个由适应度函数决定的适应度值。粒子的速度决定了粒子移动的方向和距离,速度随自身及其他粒子的移动经验进行动态调整,从而实现个体在可解空间中的寻优。
假设在一个 D D D维的搜索空间中,由 n n n个粒子组成的种群 X = ( X 1 , X 2 , ⋯ , X n ) \boldsymbol{X}=(X_1,X_2,\dotsm,X_n) X=(X1,X2,⋯,Xn),其中第 i i i个粒子表示为一个 D D D维的向量 X i = ( X i 1 , X i 2 , ⋯ , X i D ) T \boldsymbol{X_i}=(X_{i1},X_{i2},\dotsm,X_{iD})^T Xi=(Xi1,Xi2,⋯,XiD)T,代表第 i i i个粒子在 D D D维搜索空间中的位置,亦代表问题的一个潜在解。根据目标函数即可计算出每个粒子位置 X i \boldsymbol{X_i} Xi对应的适应度值。第 i i i个粒子的速度为 V = ( V i 1 , V i 2 , ⋯ , V i D ) T \boldsymbol{V}=(V_{i1},V_{i2},\dotsm,V_{iD})^T V=(Vi1,Vi2,⋯,ViD)T,其个体最优极值为 P i = ( P i 1 , P i 2 , ⋯ , P i D ) T \boldsymbol{P_i}=(P_{i1},P_{i2},\dotsm,P_{iD})^T Pi=(Pi1,Pi2,⋯,PiD)T,种群的群体最优极值为 P g = ( P g 1 , P g 2 , ⋯ , P g D ) T \boldsymbol{P_g}=(P_{g1},P_{g2},\dotsm,P_{gD})^T Pg=(Pg1,Pg2,⋯,PgD)T。
在每次迭代过程中,粒子通过个体极值和群体极值更新自身的速度和位置,即 V i d k + 1 = ω V i d k + c 1 r 1 ( P i d k − X i d k ) + c 2 r 2 ( P g d k − X i d k ) (1) V_{id}^{k+1}=\omega V_{id}^k+c_1r_1(P_{id}^k-X_{id}^k)+c_2r_2(P_{gd}^k-X_{id}^k)\tag{1} Vidk+1=ωVidk+c1r1(Pidk−Xidk)+c2r2(Pgdk−Xidk)(1) X i d k + 1 = X i d k + V k + 1 i d (2) X_{id}^{k+1}=X_{id}^k+V_{k+1_{id}}\tag {2} Xidk+1=Xidk+Vk+1id(2)其中, ω \omega ω为惯性权重; d = 1 , 2 , ⋯ , n d=1,2,\dotsm,n d=1,2,⋯,n; k k k为当前迭代次数; V i d V_{id} Vid为粒子的速度; c 1 c_1 c1和 c 2 c_2 c2是非负的常数,称为加速度因子; r 1 r_1 r1和 r 2 r_2 r2是分布于 [ 0 , 1 ] [0,1] [0,1]区间的随机数。为防止粒子的盲目搜索,一般建议将其位置和速度限制在一定的区间 [ − X m a x , X m a x ] [-X_{max},X_{max}] [−Xmax,Xmax]、 [ − V m a x , V m a x ] [-V_{max},V_{max}] [−Vmax,Vmax]。
二、案例背景
1、问题描述
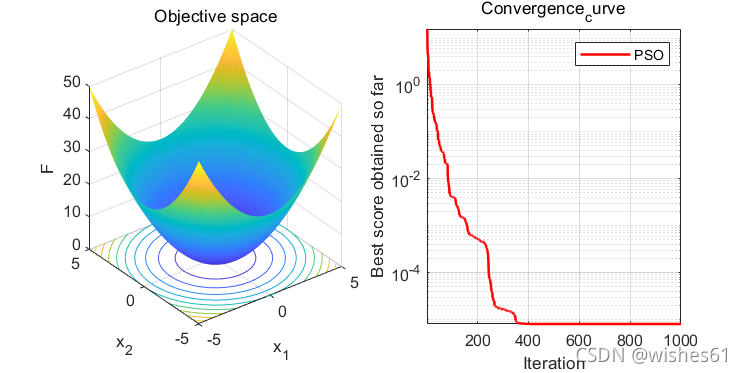
本案例寻优的非线性函数为 f ( x , y ) = s i n x 2 + y 2 x 2 + y 2 + e c o s 2 π x + c o s 2 π y 2 − 2.71289 (3) f(x,y)=\frac{sin\sqrt{x^2+y^2}}{\sqrt{x^2+y^2}}+e^{\frac{cos2\pi x+cos2\pi y}{2}}-2.71289\tag{3} f(x,y)=x2+y2sinx2+y2+e2cos2πx+cos2πy−2.71289(3)函数图形如图1所示。

从函数图形可以看出,该函数有很多局部极大值点,而极限位置为 ( 0 , 0 ) (0,0) (0,0),在 ( 0 , 0 ) (0,0) (0,0)附近取得极大值,极大值约为1.0054。
2、解题思路及步骤
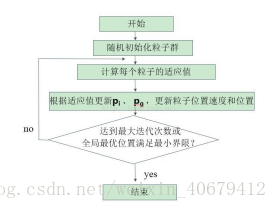
基于PSO算法的函数极值寻优算法流程图如图2所示。

其中,粒子和速度初始化是随机初始化粒子速度和粒子位置;根据式(3)计算粒子适应度值;根据初始粒子适应度值确定个体极值和群体极值;根据式(1)与式(2)更新粒子速度和位置;根据新种群中粒子适应度值更新个体极值和群体极值。
本案例中,适应度函数为函数表达式,适应度值为函数值。种群粒子数为20,每个粒子的维数为2,算法迭代进化次数为300。
三、MATLAB程序实现
1、PSO算法参数设置
设置PSO算法的运行参数,程序代码如下:
%% 清空环境
clc
clear%% 参数初始化
% 速度更新参数
c1 = 1.49445;
c2 = 1.49445;maxgen = 300; % 进化次数
sizepop = 20; % 种群规模% 个体和速度的最大最小值
popmax=2; popmin=-2;
Vmax=0.5; Vmin=-0.5;
2、种群初始化
随机初始化粒子位置和粒子速度,并根据适应度函数计算粒子适应度值。程序代码如下:
%% 随机产生初始粒子和速度
for i = 1:sizepop% 随机产生一个种群pop(i, :) = 2*rands(1, 2); % 初始种群V(i, :) = 0.5*rands(1, 2); % 初始化速度% 计算适应度fitness(i) = fun(pop(i, :)); % 染色体的适应度
end
适应度函数如下:
function y = fun(x)
% 函数用于计算粒子适应度值
% x input 输入粒子
% y output 粒子适应度值
y=sin( sqrt(x(1).^2+x(2).^2) )./sqrt(x(1).^2+x(2).^2)+...exp((cos(2*pi*x(1))+cos(2*pi*x(2)))/2)-2.71289;
3、寻找初始极值
根据初始粒子适应度值寻找个体极值和群体极值。
%% 个体极值和群体极值
[bestfitness, bestindex] = max(fitness);
zbest = pop(bestindex, :); % 全局最佳
gbest = pop; % 个体最佳
fitnessgbest = fitness; % 个体最佳适应度值
fitnesszbest = bestfitness; % 全局最佳适应度值
4、迭代寻优
根据式(1)与式(2)更新粒子位置和速度,并且根据新粒子的适应度值更新个体极值和群体极值。程序代码如下:
%% 迭代寻优
for i=1:maxgen% 粒子位置和速度更新for j=1:sizepop% 速度更新V(j,:) = V(j,:) + c1*rand*(gbest(j, :) - pop(j, :)) + c2*rand*(zbest - pop(j, :));V(j, find(V(j, :) > Vmax)) = Vmax;V(j, find(V(j, :) < Vmin)) = Vmin;% 种群更新pop(j, :) = pop(j, :)+V(j, :);pop(j, find(pop(j, :) > popmax)) = popmax;pop(j, find(pop(j, :) < popmin)) = popmin;% 适应度值fitness(j) = fun(pop(j, :)); end%% 个体和群体极值更新for j = 1:N% 个体最优更新if fitness(j) < fitnesspbest(j)pbest(j, :) = X(j, :);fitnesspbest(j) = fitness(j);end% 群体最优更新if fitnesspbest(j) > fitnessgbestgbest = pbest(j, :);fitnessgbest = fitnesspbest(j);endend% 每代最优值记录到yy数组中yy(i) = fitnesszbest;
end
5、结果分析
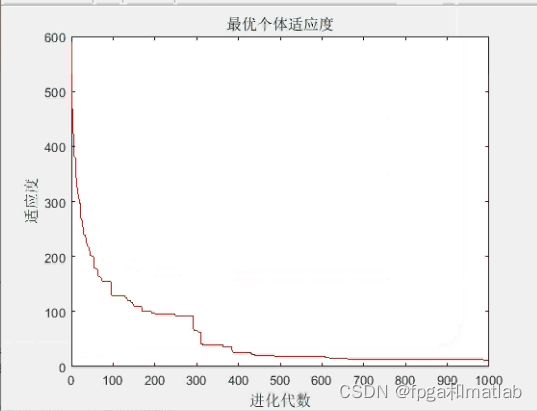
PSO算法反复迭代300次,画出每代最优个体适应度值变化图象。程序代码如下:
%% 画出每代个体最优适应度值
disp(['最优位置:', num2str(zbest)]);
disp(['最优极值:', num2str(fitnesszbest)]);
plot(yy)
title('最优个体适应度', 'fontsize', 12);
xlabel('进化代数', 'fontsize', 12);
ylabel('适应度', 'fontsize', 12);
Command Window中显示的结果为:
最优位置:-0.00015399 -0.00068763
最优极值:1.0054
最优个体适应度值变化如图3所示。

最终得到的最优个体适应度值为1.0054,对应的粒子位置为(-0.00015399,-0.00068763),PSO算法寻优得到最优值接近函数实际最优值,说明PSO算法具有较强的函数极值寻优能力。
四、惯性权重
1、惯性权重的选择
惯性权重 ω \omega ω体现的是粒子继承先前的速度的能力,Shi.Y最先将惯性权重 ω \omega ω引入PSO算法中,并分析指出一个较大的惯性权值有利于全局搜索,而一个较小的惯性权值则更利于局部搜索。为了更好地平衡算法的全局搜索与局部搜索的能力,Shi.Y提出了线性递减惯性权重(Linear decreasing inertia weight,LDIW),即 ω ( k ) = ω s t a r t − ( ω s t a r t − ω e n d ) ( T m a x − k ) / T m a x (4) \omega(k)=\omega_{start}-(\omega_{start}-\omega_{end})(T_{max}-k)/T_{max}\tag{4} ω(k)=ωstart−(ωstart−ωend)(Tmax−k)/Tmax(4)其中, ω s t a r t \omega_{start} ωstart为初始惯性权重; ω e n d \omega_{end} ωend为迭代至最大迭代次数时的惯性权重; k k k为当前迭代次数; T m a x T_{max} Tmax为最大迭代次数。一般来说,惯性权重 ω s t a r t = 0.9 , ω e n d = 0.4 \omega_{start}=0.9,\omega_{end}=0.4 ωstart=0.9,ωend=0.4时算法性能最好。这样,随着迭代次数的增大,惯性权重由0.9线性递减至0.4,迭代初期较大的惯性权重使得算法保持了较强的全局搜索能力,而迭代后期较小的惯性权重有利于算法进行更精准的局部搜寻。线性惯性权重只是一种经验做法,常用的惯性权重的选择还包括以下几种: ω ( k ) = ω s t a r t − ( ω s t a r t − ω e n d ) ( k T m a x ) 2 (5) \omega(k)=\omega_{start}-(\omega_{start}-\omega_{end})(\frac{k}{T_{max}})^2\tag{5} ω(k)=ωstart−(ωstart−ωend)(Tmaxk)2(5) ω ( k ) = ω s t a r t + ( ω s t a r t − ω e n d ) [ 2 k T m a x − ( k T m a x ) 2 ] (6) \omega(k)=\omega_{start}+(\omega_{start}-\omega_{end})[\frac{2k}{T_{max}}-(\frac{k}{T_{max}})^2]\tag{6} ω(k)=ωstart+(ωstart−ωend)[Tmax2k−(Tmaxk)2](6) ω ( k ) = ω e n d ( ω s t a r t ω e n d ) 1 / ( 1 + c k / T m a x ) (7) \omega(k)=\omega_{end}(\frac{\omega_{start}}{\omega_{end}})^{1/(1+ck/T_{max})}\tag{7} ω(k)=ωend(ωendωstart)1/(1+ck/Tmax)(7)几种 ω \omega ω的动态变化如图4所示。

2、 ω \omega ω变化的算法性能分析
算法参数设置:种群规模20,进化300代。每个实验设置运行100次,将100次的平均值作为最终结果。
在上述的参数设置下,运用5种 ω \omega ω取值方法对函数进行求解,并比较所得解的平均值、失效次数和接近最优值的次数,来分析其收敛精度、收敛速度等性能。
每种 ω \omega ω的算法进化曲线如图5所示。

本案例中,将距离最优解1.0054误差为0.01的解视为接近最优解,将0.8477及更小的解视为陷入局部最优解。
由图5和表1可以看出,惯性权重 ω \omega ω不变的粒子群优化算法虽然具有较快的收敛速度,但其后期容易陷入局部最优,求解精度低;而几种 ω \omega ω动态变化的算法虽然在算法初期收敛稍慢,但在后期局部搜索能力强,利于算法跳出局部最优而求的最优解,提高了算法的求解精度。
式(5) ω \omega ω动态变化方法,前期 ω \omega ω变化较慢,取值较大,维持了算法的全局搜索能力;后期 ω \omega ω变化较快,极大地提高了算法的局部搜索能力,从而取得了很好的求解效果。

五、参考文献
[1] J. Kennedy, R. Eberhart. Particle swarm optimization[C]. Proceedings of ICNN’95 - International Conference on Neural Networks, 1995, 4: 1942-1948.
[2] 张选平, 杜玉平, 秦国强, 等. 一种动态改变惯性权的自适应粒子群算法[J]. 西安交通大学学报, 2005(10): 1039-1042.
[3] 郁磊, 史峰, 王辉, 等. MATLAB智能算法30个案例分析(第2版)[M]. 北京: 北京航空航天大学出版社, 2015.