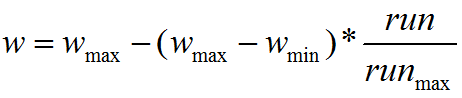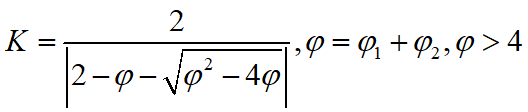1算法简介
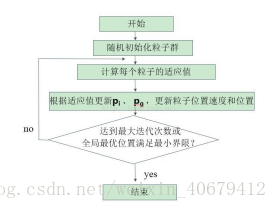
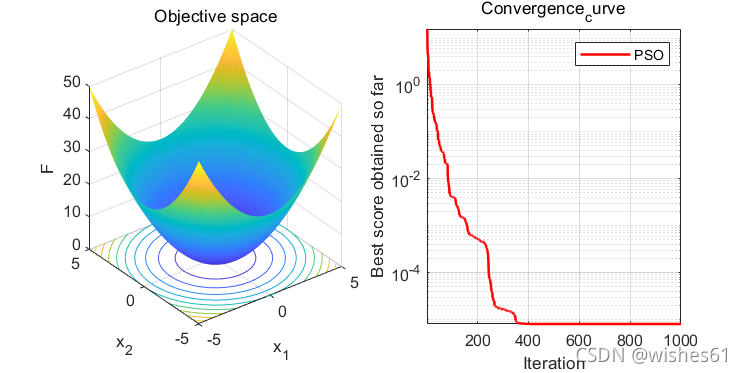
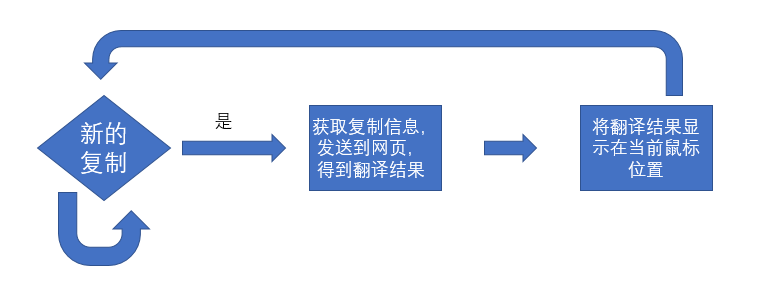
粒子群优化算法,在1995年由Eberhart博士和kennedy博士提出,源于对鸟群捕食的行为研究。该算法最初是受到飞鸟集群活动的规律性启发,进而利用群体智能建立的一个简化模型。算法流程图如下所示。

核心公式( 更新速度和位置):
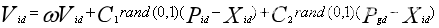
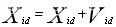
这里 w \ w w称为惯性因子, C 1 \ C1 C1 和 C 2 \ C2 C2 称为加速常数,一般取 [ 0 , 4 ] \ [0,4] [0,4] 。 P i d \ Pid Pid 表示第 i \ i i 个变量的个体极值的第 d \ d d 维。 P g d \ Pgd Pgd 表示全局最优解的第 d \ d d维。
2 算法优缺点
PSO算法是一种随机的、并行的优化算法。
优点 是:不要求被优化函数具有可微、可导、连续等性质,收敛速度较快,算法简单,容易编程实现。
然而,PSO算法的 缺点 在于:
(1)对于有多个局部极值点的函数,容易陷入到局部极值点中,得不到正确的结果。
造成这种现象的原因有两种,其一是由于待优化函数的性质;其二是由于微粒群算法中微粒的多样性迅速消失,造成早熟收敛。这两个因素通常密不可分地纠缠在一起。
(2)由于缺乏精密搜索方法的配合,PSO算法往往不能得到精确的结果。
造成这种问题的原因是PSO算法并没有很充分地利用计算过程中获得的信息,在每一步迭代中,仅仅利用了群体最优和个体最优的信息。
(3)PSO算法虽然提供了全局搜索的可能,但是并不能保证收敛到全局最优点上。
因此,PSO算法一般适用于一类高维的、存在多个局部极值点而并不需要得到很高精度解的优化问题。
3 算法原理伪代码(matlab)
for i=1:Nfor j=1:Dx=xmin+rand(N,D)*(xmax-xmin); %随机初始化位置v=rand(N,D); %随机初始化速度end end%------先计算各个粒子的适应度,并初始化Pi和Pg---------------------- for i=1:Np(i)=fitness(x(i,:)); %计算初始粒子的适应度值y(i,:)=x(i,:); %个体极值中的变量值等于粒子的初始值---为了后期进行保存全局最优值 end pg=x(N,:); %Pg为全局最优值---将初始位置的最后一列元素赋给全局最优值---目的在于保存全局最优值 for i=1:(N-1)if fitness(x(i,:)) <fitness(pg) pg=x(i,:); %更新全局最优值,保存最优值end end%------进入主要循环,按照公式依次迭代,直到满足精度要求------------ for t=1:M %做一个主循环,用于迭代time(t)=t;for i=1:N %更新速度、位移v(i,:)=w*v(i,:)+c1*rand*(y(i,:)-x(i,:))+c2*rand*(pg-x(i,:));if v(i,:)<xmin %防止越界v(i,:)=xmin;endif v(i,:)>xmaxv(i,:)=xmax;end x(i,:)=x(i,:)+v(i,:); % 更新之后的点if fitness(x(i,:))< p(i) % 使用选择函数p(i)=fitness(x(i,:));y(i,:)=x(i,:);%更新个体极值 endif p(i)<fitness(pg) %选择保存最优值pg=y(i,:);% pg=x(i,:);end endPbest(t)=fitness(pg); %将全局最优值赋给Pbest end