如何从在安卓Android手机获取微信小程序源代码

获取微信小程序源代码两种方法：

1、在手机中获取。但需要获取手机的root权限，获得微信小程序的wxapkg包；
2、运用模拟器，在电脑上运行微信小程序，获得微信小程序的wxapkg包；

第一个方法有点难，下文以第二种方法展开。

使用到的工具：

1、“电脑端的安卓模拟器”安装包：推荐使用“夜神模拟器”，可从其官方网站获得该安装包：https://www.yeshen.com/；
2、微信.apk：可从其官方网站获得该安装包：https://weixin.qq.com/；
3、RE管理器.apk：给我留言获得（这类资源经常被和谐）；
4、“Node.js”安装包:可从其官方网站获得该安装包：http://nodejs.cn/download/；
5、反编译的脚本：给我留言获得（这类资源经常被和谐）。

步骤一：在Windows下，安装“夜神安卓模拟器”

1.1 找到“夜神安卓模拟器”的官方网站：https://www.yeshen.com/；

1.2 在其官方首页中，下载最新的夜神安卓模拟器安装包，进行下载；

1.3 双击安装包，开始安装夜神安卓模拟器。安装过程中无特殊操作，等待提示“安装完成“；

步骤二：在模拟器中，安装“微信”App

2.1 双击运行“夜神安卓模拟器”（打开后效果如下）。

###

2.2 利用“夜神安卓模拟器”的浏览器，下载最新版本的“微信”(微信版本版本过低，会导致无法使用微信)。

2.3 在浏览器的地址栏输入微信官方网址：https://weixin.qq.com/,并敲回车键，打开该网站，找到下载微信的按钮；

2.4 和手机一样，下拉顶部显示相关信息。单击弹出项，开始安装微信（和手机上一样）；

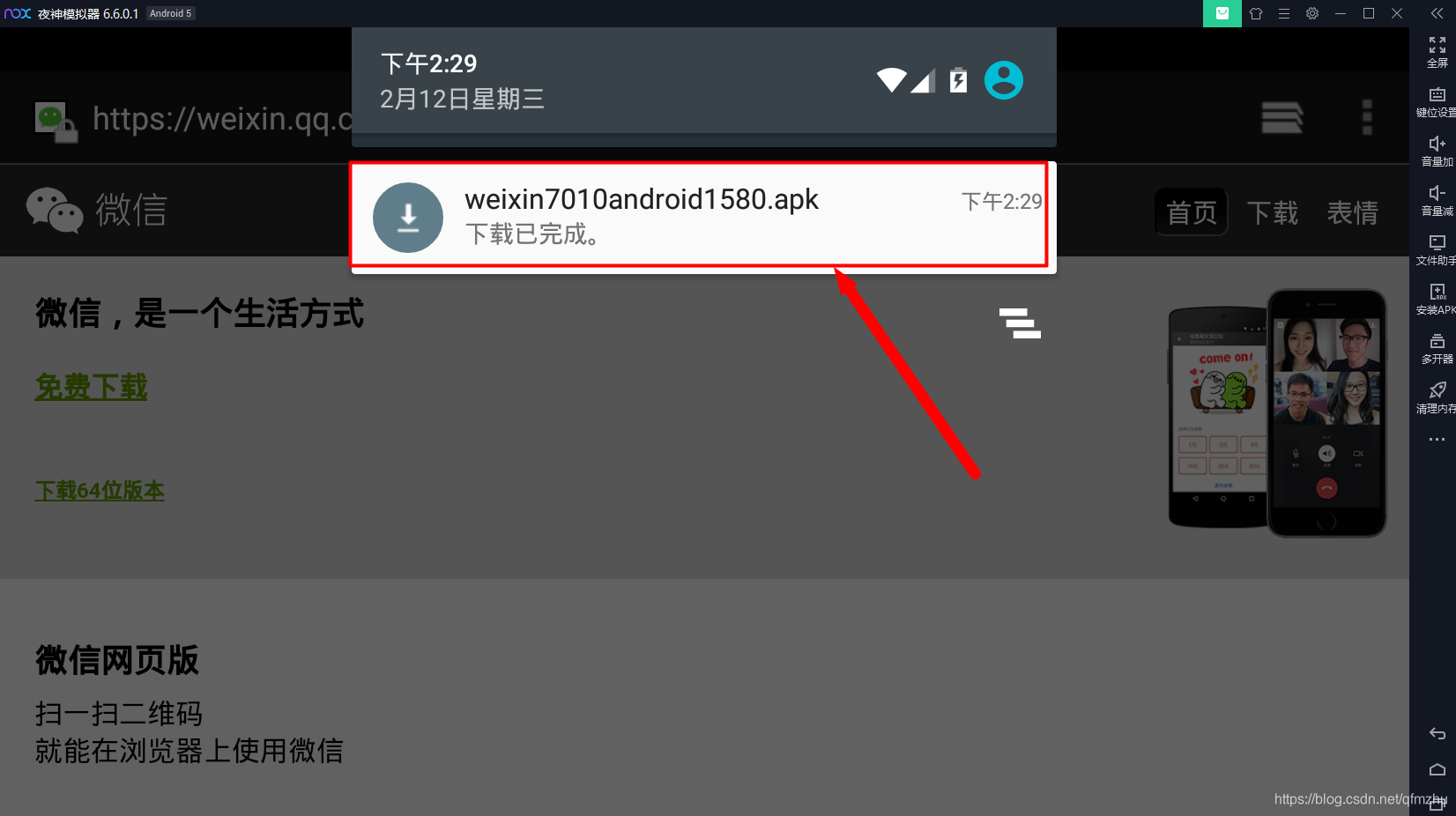
2.5 鼠标单击模拟器右下角“主页”按钮，返回模拟器主界面。会看到安卓好的微信；

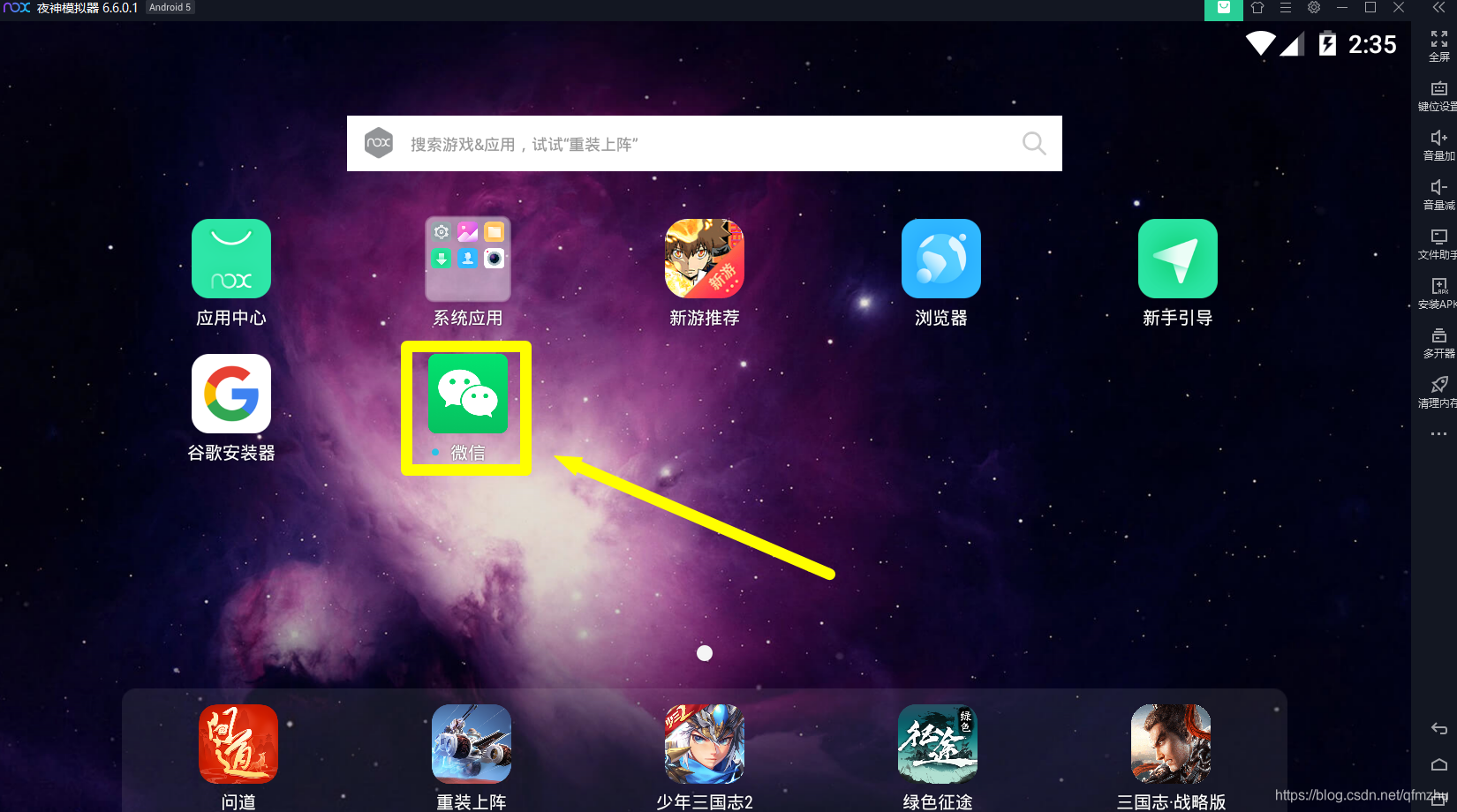
步骤三：在模拟器中登录微信，并打开需要获取源码的“小程序”

3.1 在模拟器中，登录微信。

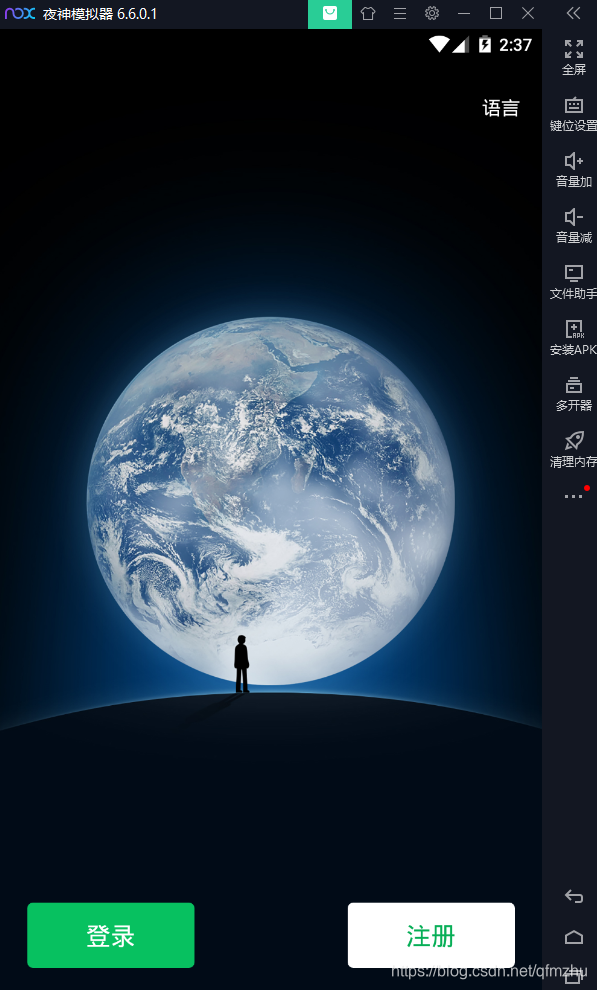
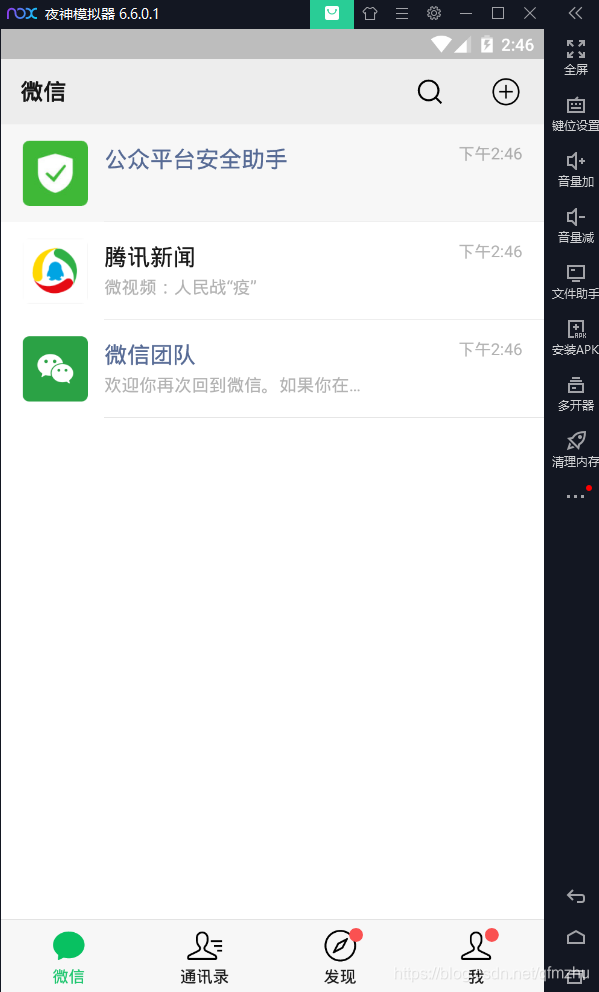
3.2 在微信的小程序中，搜索需要获取源代码的“小程序名称”，并打开。以“进制转换器”为例；

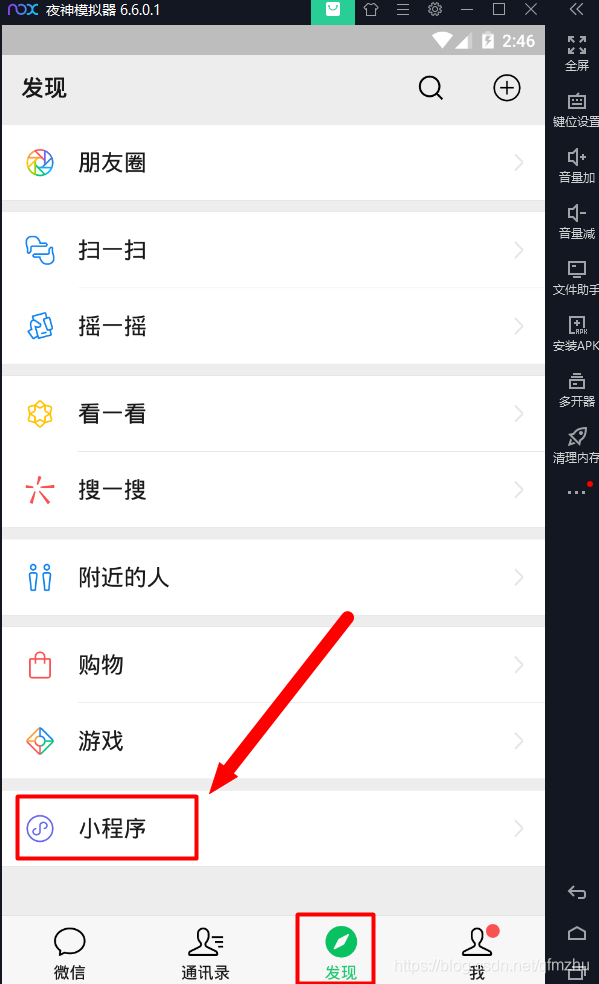
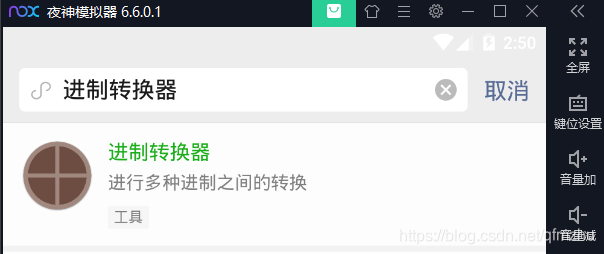
步骤四：在模拟器中，安装“Re管理器”App

4.1 获取“RE管理器.apk”可以向我留言，暂不提供下载路径，担心被和谐。

4.2 在模拟器中，安装“RE管理器.apk”。在模拟器的右侧有一个“安装APK”选项，找到“RE管理器.apk”在电脑中的存放路径，安装该App。

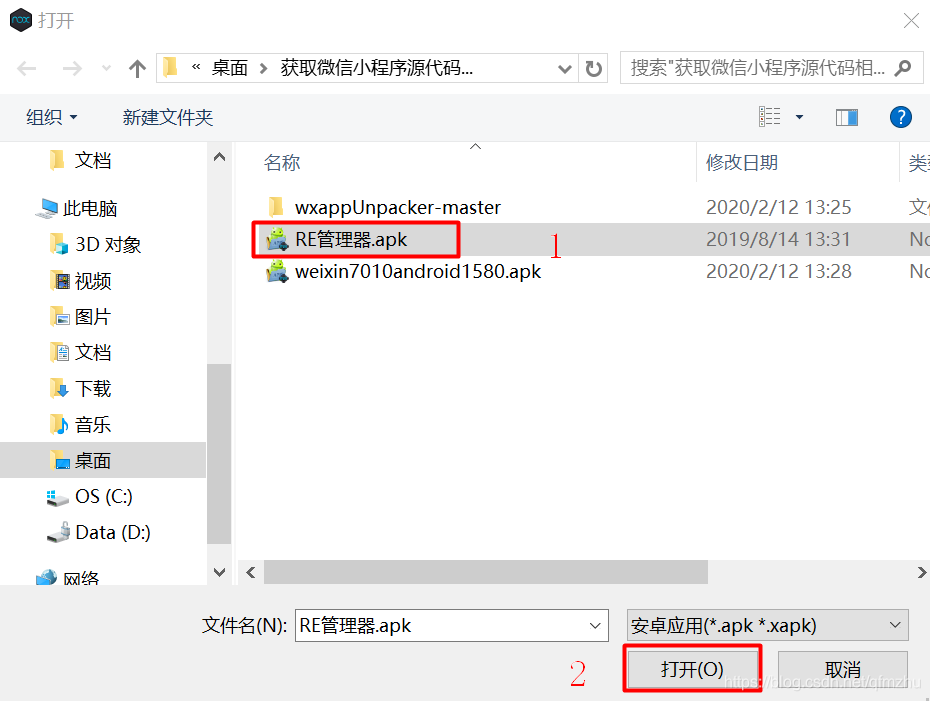
4.3 在模拟器中，打开“RE管理器.apk”。打开时候需要获取权限，允许授权即可。

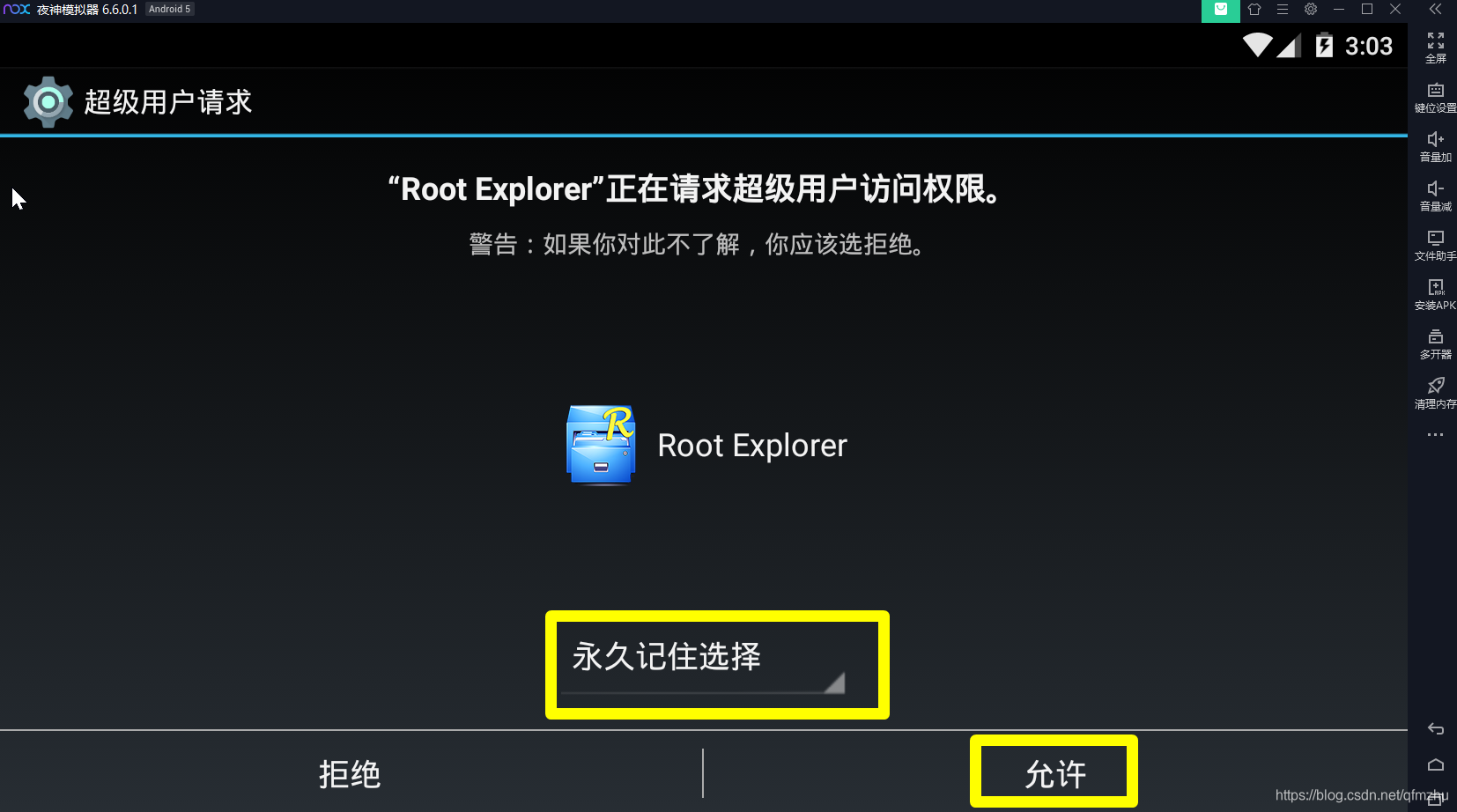
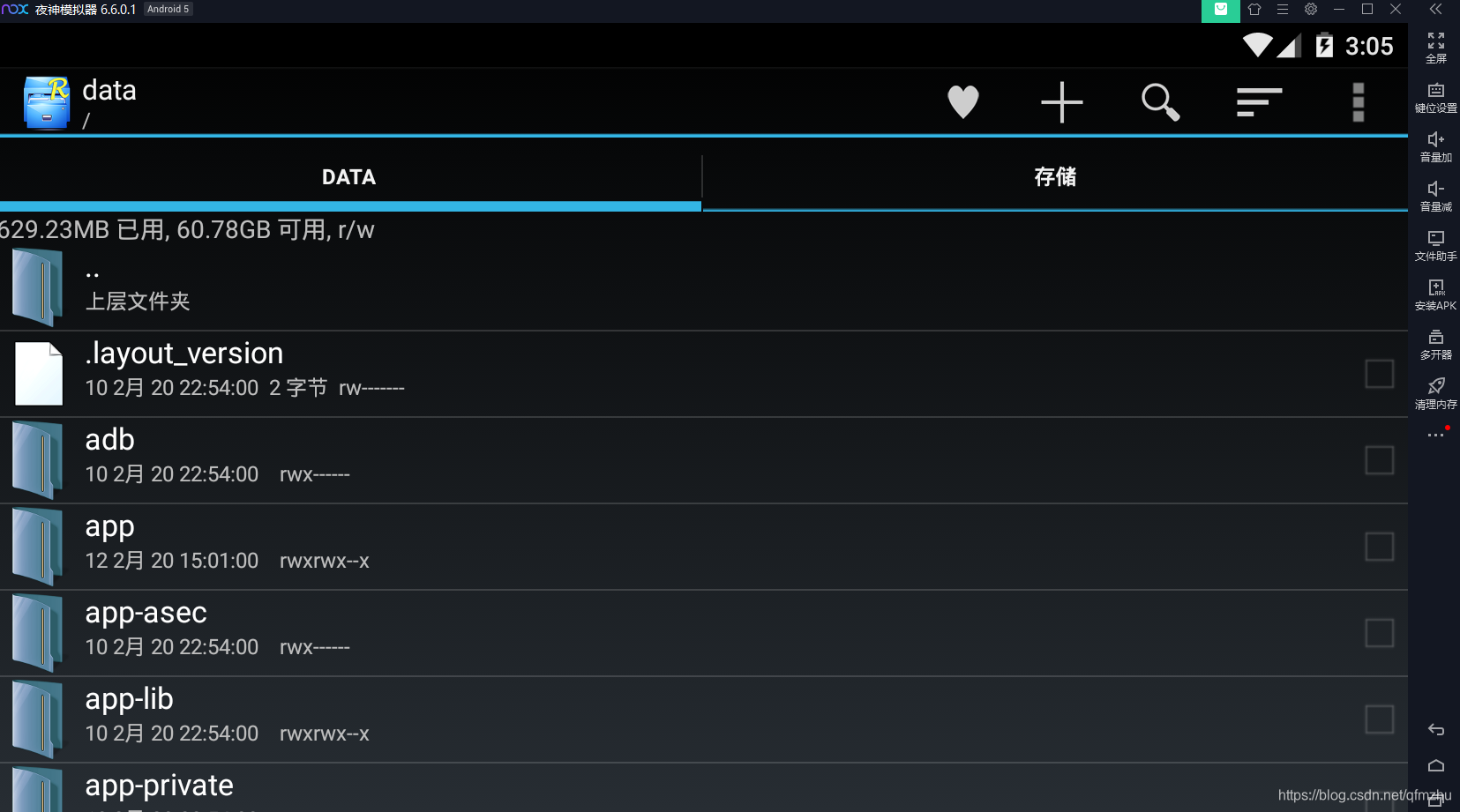
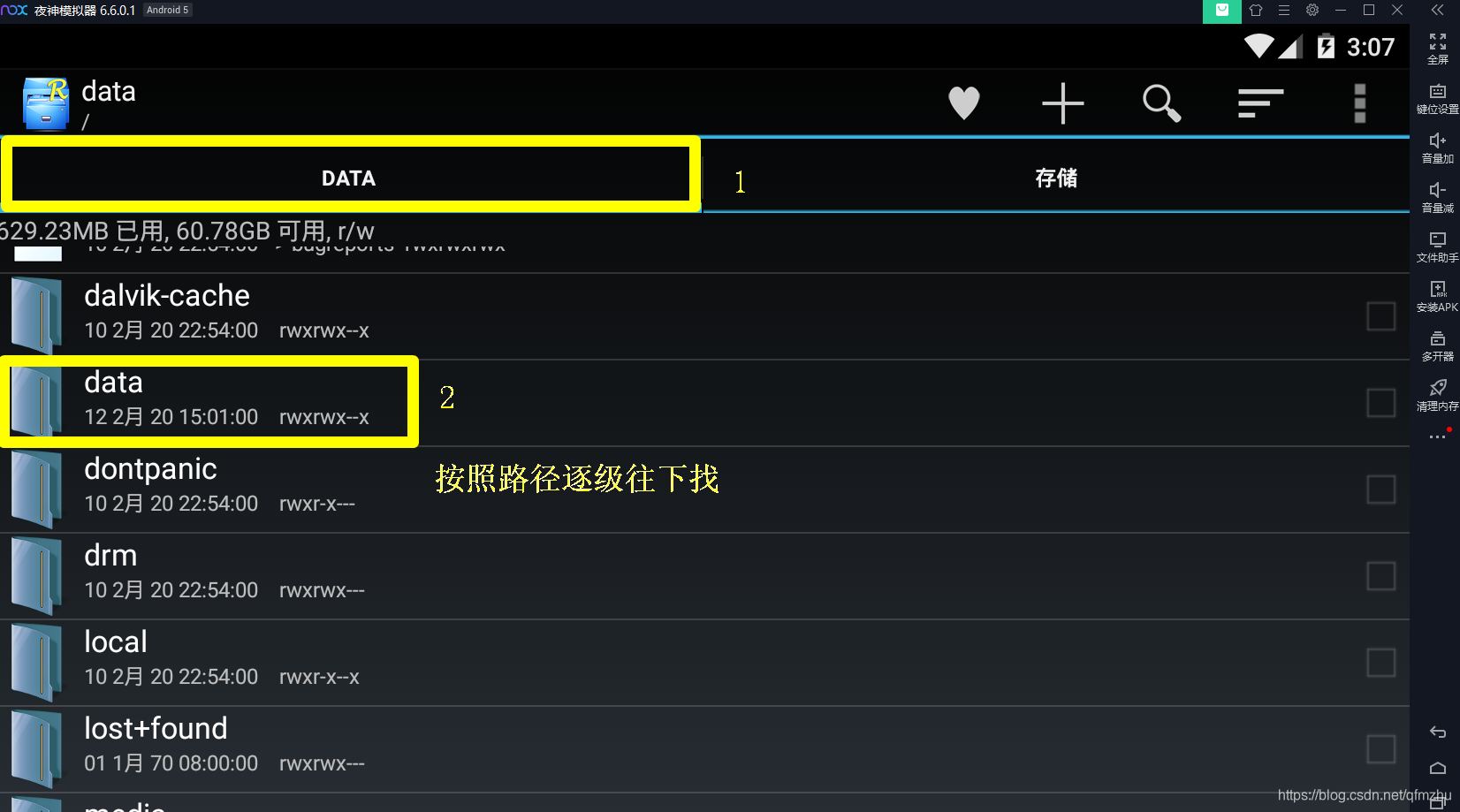
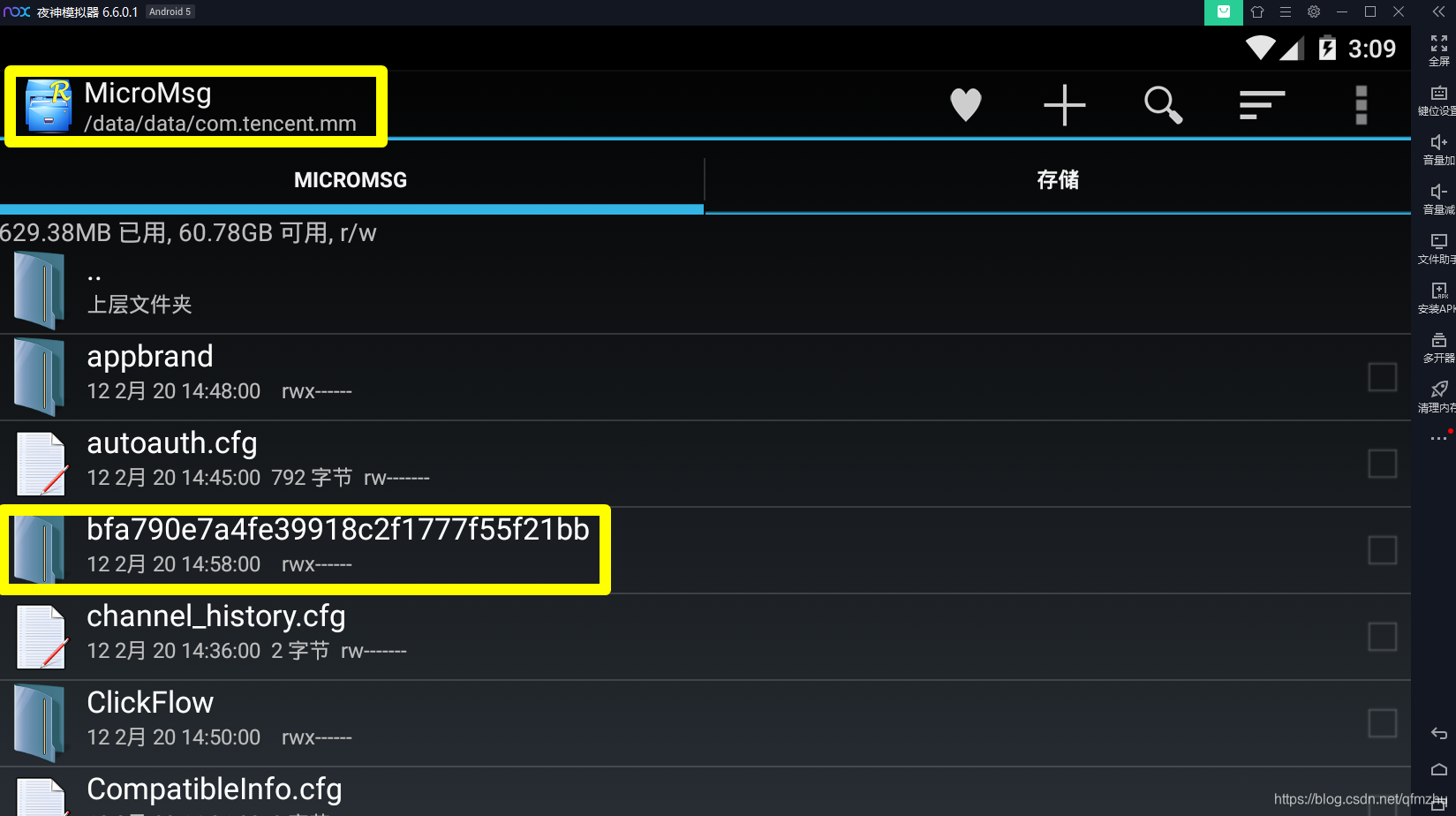
4.4 在“RE管理器”中，找到存放小程序源代码的目录/data/data/com.tencent.mm/MicroMsg/appbrand（类似一个a8b3488516c9d81e1d5f511891583cf9文件，别的教程是不会告诉你的）/pkg/就抵达了目的文件夹。

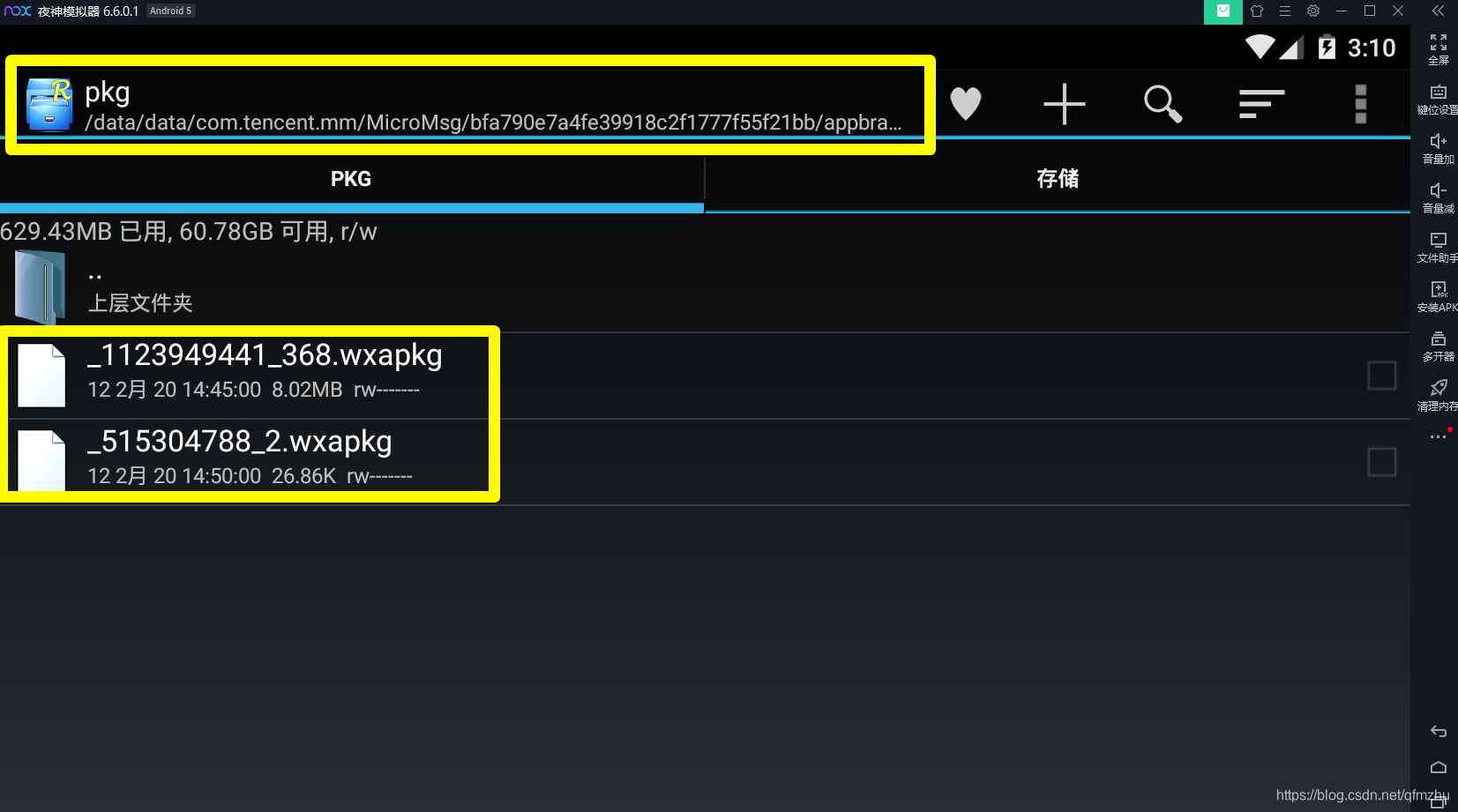
4.5 选中“*.wxapkg”文件，对这些文件进行压缩；

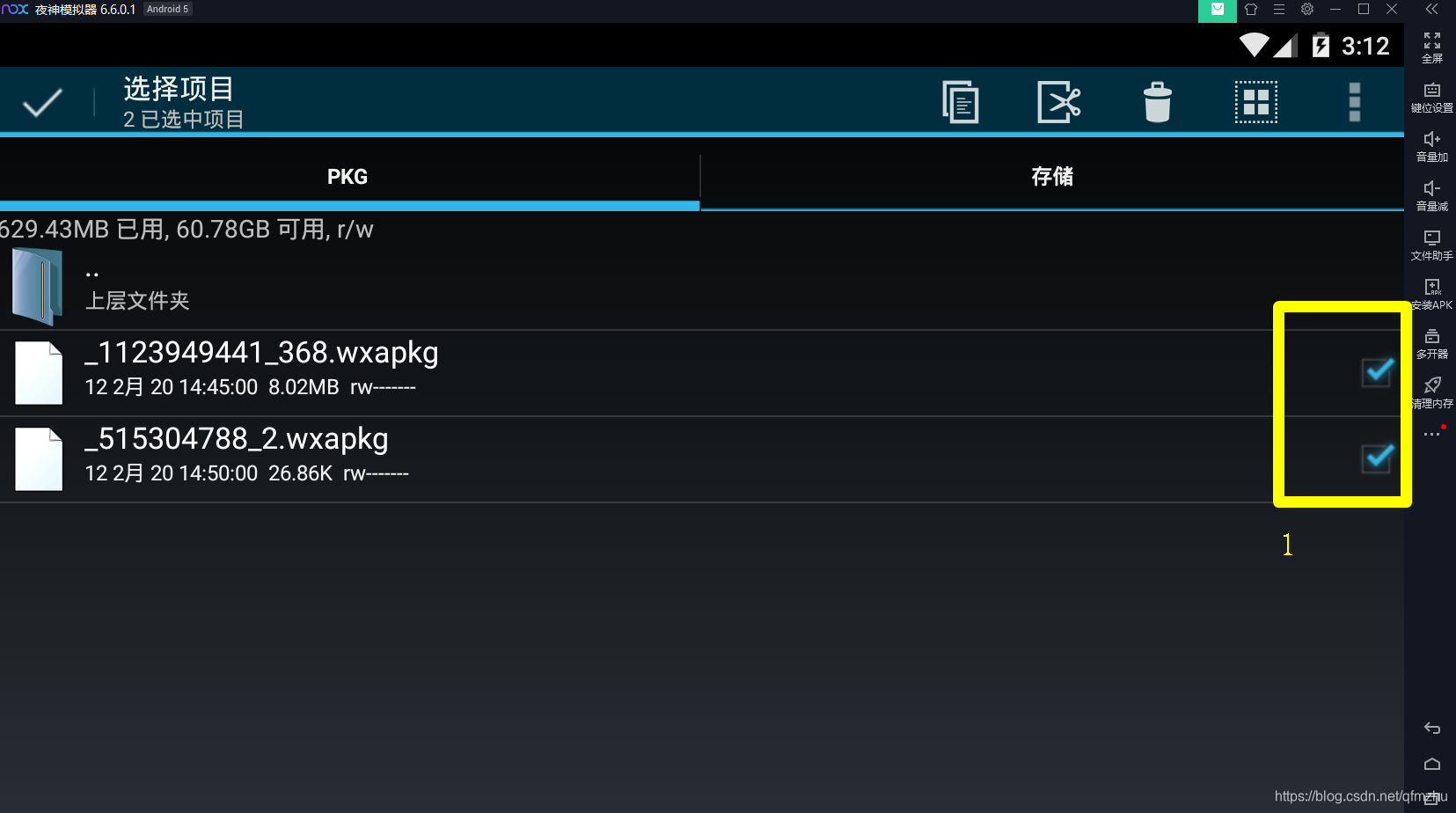
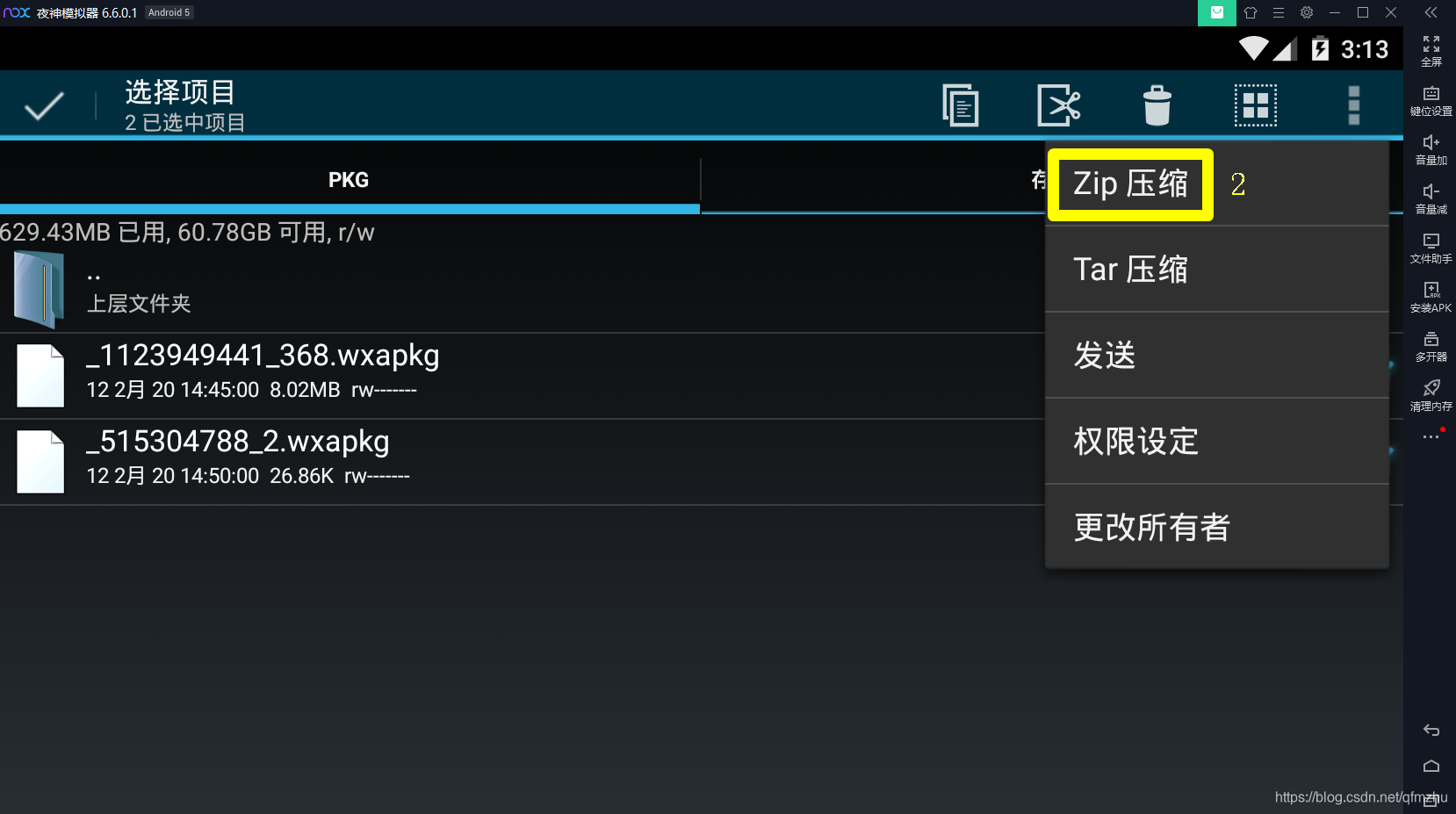
4.6 将压缩后的文件，发送至“邮箱”或者“微信”，从而获得小程序源代码；

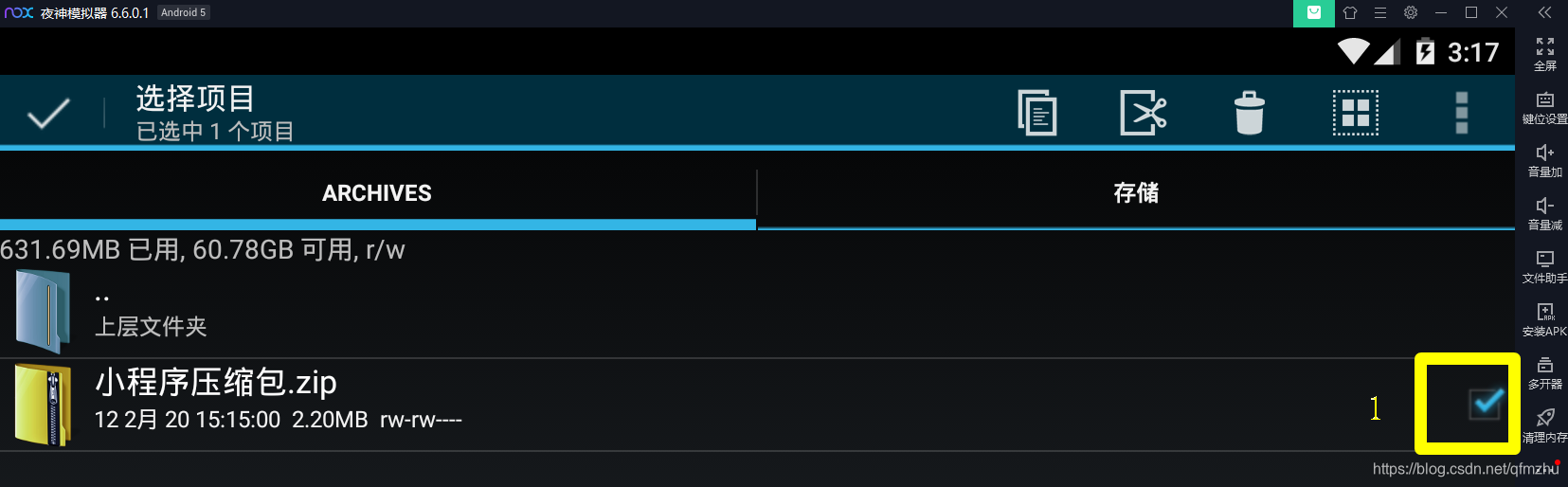
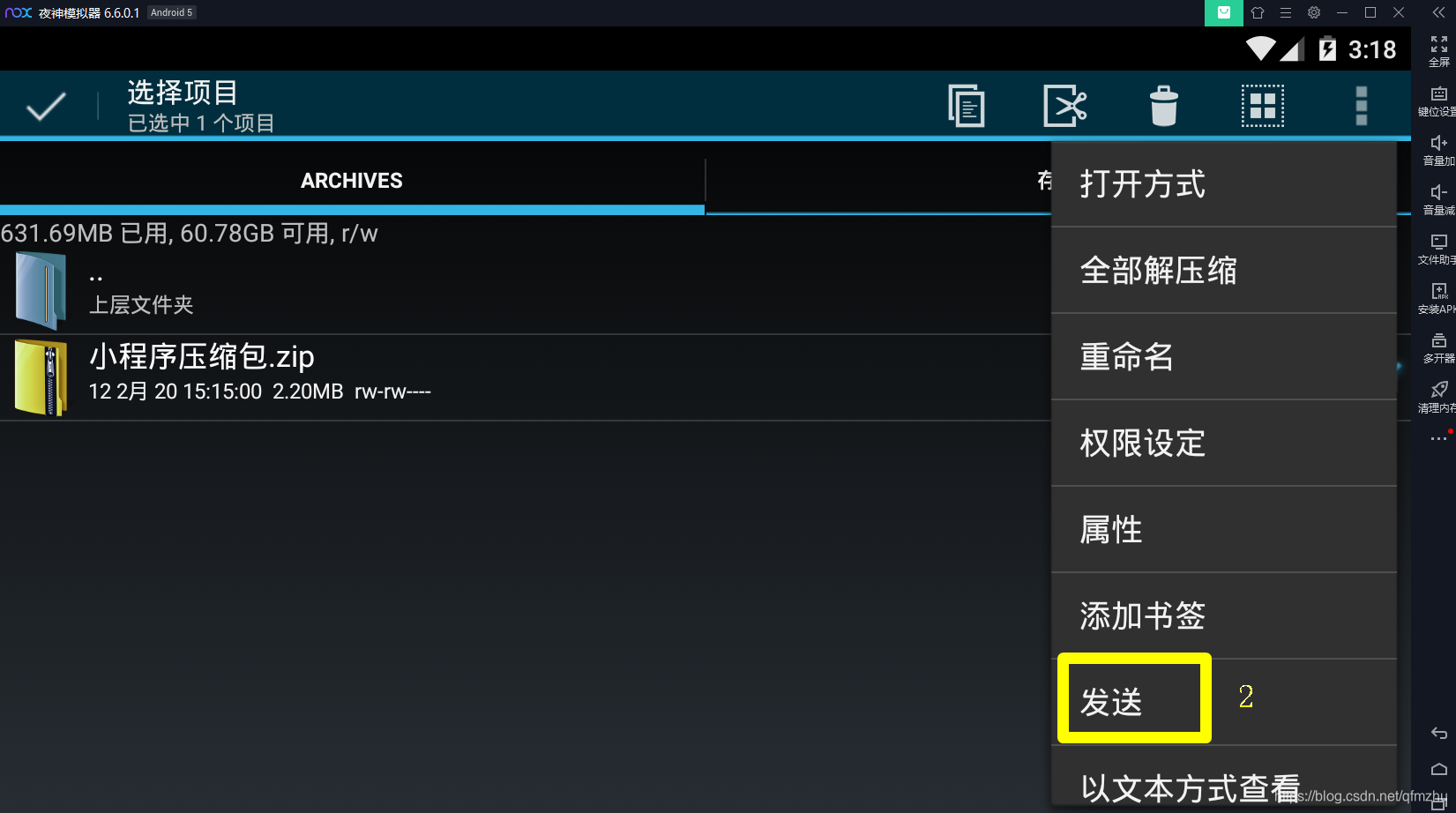
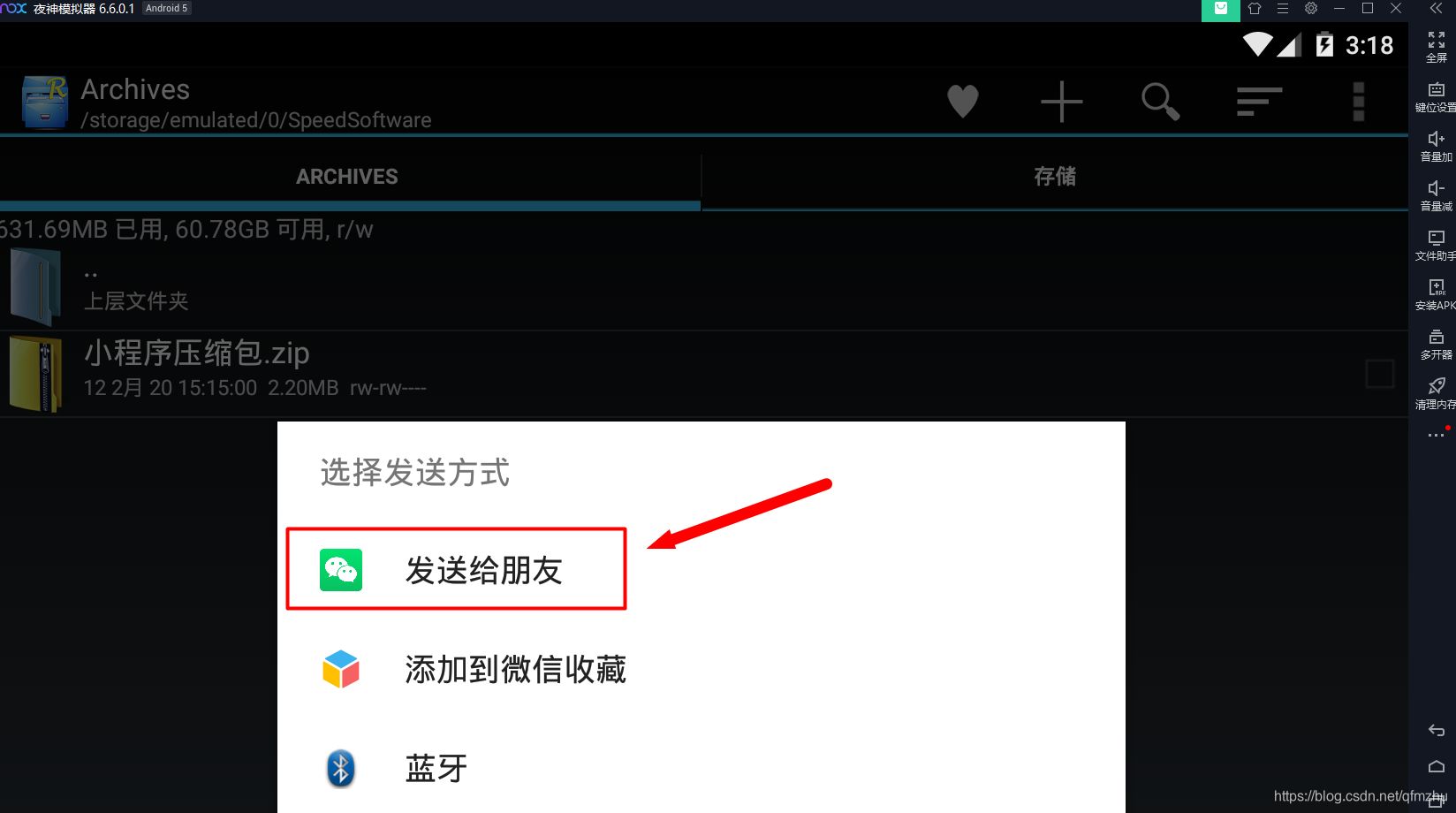
步骤五：下载并打开“Node.js”

5.1 “Node.js”官方网站：http://nodejs.cn/download/，下载适合自己的版本，并打开“Node.js”

步骤六：使用反编译脚本解包 wxapkg，获得小程序源代码

假设"*.wxapkg"存放在“C:\Users******\Desktop\abc\wxappUnpacker-master”路径下。在打开的node.js中依次输入相应的指令：

6.1 cd 到你clone或者下载好的反编译脚本目录下，输入指令：cd C:\Users***\Desktop\abc\wxappUnpacker-master；

6.2 输入指令：npm install esprima；

6.3 输入指令：npm install css-tree

6.4 输入指令：npm install cssbeautify；

6.5 输入指令：npm install vm2；

6.6 输入指令：“npm install uglify-es”;

6.7 输入指令：npm install js-beautify;

6.8 输入指令：npm install escodegen -g;

6.9 安装好依赖之后，反编译 .wxapkg 文件；

在当前目录下输入：
node wuWxapkg.js [-d] <files…> //files 就是你想要反编译的文件名
例如：我有一个需要反编译的文件 _-70156332_3.wxapkg已经解压到了D盘根目录下,那么就输出命令：
node wuWxapkg.js D:_-70156332_3.wxapkg

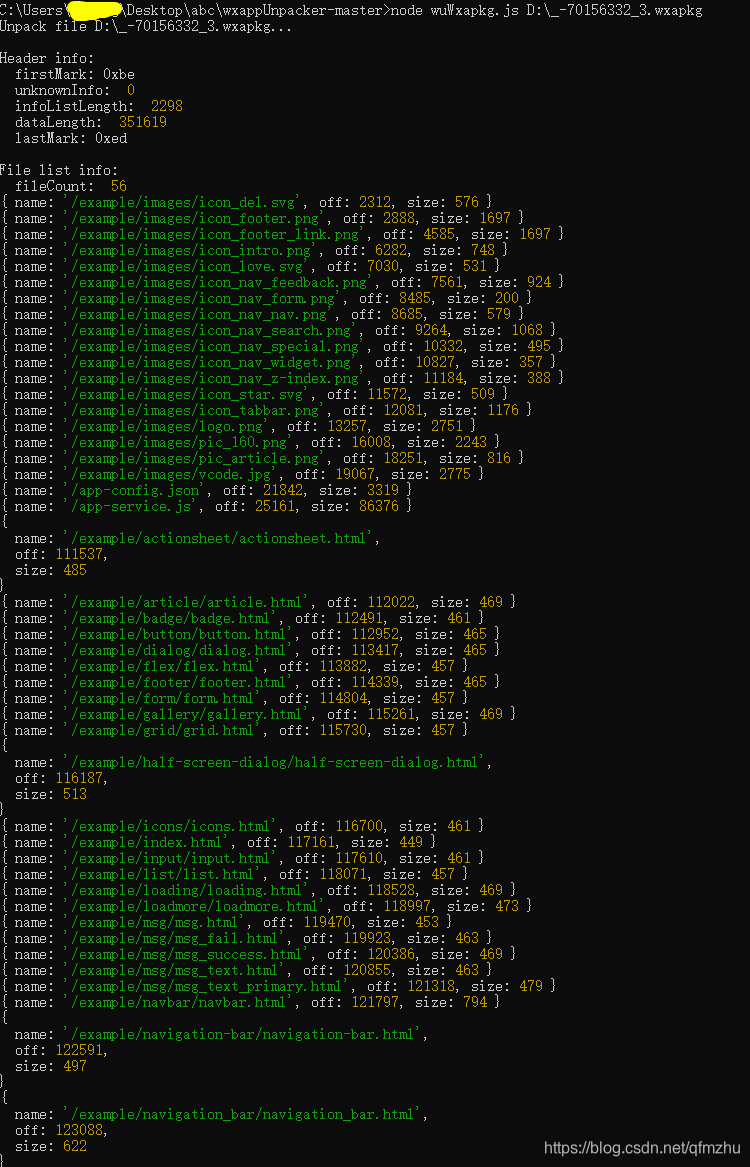
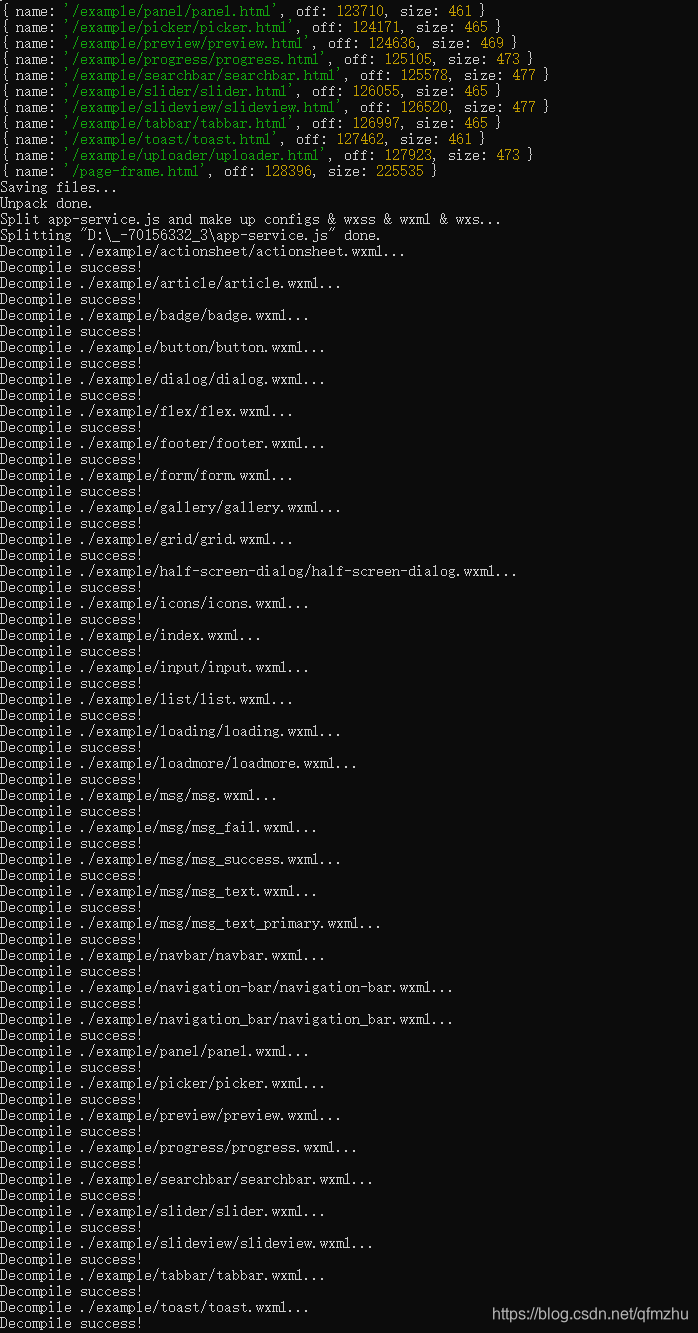
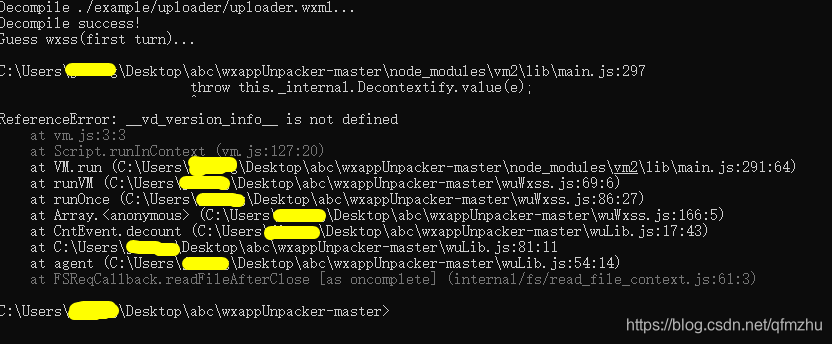
6.10 完成（6.9）后，在“*.wxapkg ” 文件的相同路径下，生成一个同名的文件夹，获得小程序源代码;

欢迎大家给我留言！！！
或关注我的微信公众号：汽车电子助手

END