1. 随机事件
1.1. 概念
1.1.1. 随机现象
在一定的条件下,并不总是出现相同的结果的现象称为随机现象,如抛一枚硬币与掷一颗骰子。随机现象有两个特点:
- 结果不止一个;
- 哪一个结果出现,人们事先不知道。
只有一个结果的现象称为确定性现象。
1.1.2. 样本空间
随机现象的一切可能基本结果组成的集合称为样本空间,即为 Ω = { ω } \Omega=\{\omega\} Ω={ω},其中 ω \omega ω表示基本结果,又称为样本点。需要注意的是:
- 样本空间中的元素可以是数,也可以不是数。
- 样本空间至少有两个样本点,仅含两个样本点的样本空间是最简单的样本空间。
- 从样本空间含有样本点的个数区分,样本空间可以分为有限与无限两类。另外,往往将样本点的个数为有限个或可列个的情况归为一类,称为离散样本空间。而将样本点的个数为不可列无限个的情况归为另一类,称为连续样本空间。
1.1.3. 随机事件
随机现象的某些样本点组成的集合称为随机事件,简称事件,常用大写字母 A , B , C , ⋯ A,B,C,\cdots A,B,C,⋯表示。要注意以下几点:
- 任一事件 A A A是相应样本空间的一个子集。
- 当子集 A A A中某个样本点出现了,就说事件 A A A发生了。
- 事件可以用集合表示,也可以用明白无误的语言描述。
- 由样本空间 Ω \Omega Ω中的单个元素组成的子集称为基本事件。而 Ω \Omega Ω称为必然事件,空间 ∅ \emptyset ∅称为不可能事件。
1.1.4. 随机变量
用来表示随机现象结果的变量称为随机变量,常用大写字母 X , Y , Z , ⋯ X,Y,Z,\cdots X,Y,Z,⋯表示。很多事件都可用随机变量表示,表示时关键应写明随机变量的含义。
例如:掷一颗骰子,可能出现1,2,3,4,5,6诸点,若设置 X = X= X=“掷一颗骰子出现的点数”,则随机变量 X X X的可能取值为1,2,3,4,5,6,这时
- 事件“出现3点”可用“ X = 3 X=3 X=3”表示。
- 事件“出现点数超过3”可用“ X > 3 X>3 X>3”表示。
- “ X ≤ 6 X\leq 6 X≤6”是必然事件 Ω \Omega Ω.
- “ X = 7 X=7 X=7”是不可能事件 ∅ \emptyset ∅.
1.1.5. 事件间的关系
一、包含关系
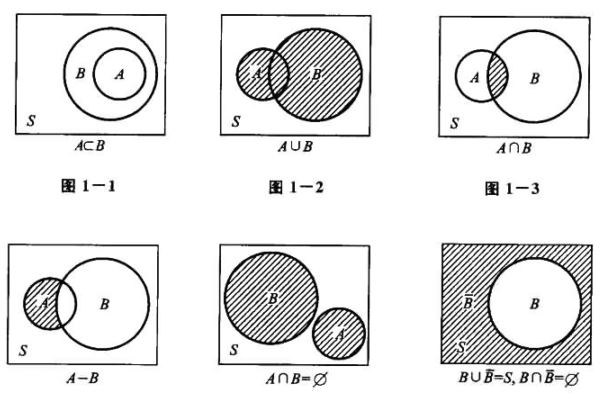
如果属于 A A A的样本点必属于 B B B,则称 A A A被包含在 B B B中,或称 B B B包含 A A A,记为 A ⊂ B A\subset B A⊂B.用概率论的语言说:事件 A A A发生必然导致事件 B B B发生。
二、相等关系
如果事件 A A A与事件 B B B满足:属于 A A A的样本点必属于 B B B,而且属于 B B B的样本点必属于 A A A,即 A ⊂ B A\subset B A⊂B且 B ⊂ A B\subset A B⊂A,则称事件 A A A与 B B B相等,即为 A = B A=B A=B.
三、互不相容
如果事件 A A A与事件 B B B没有相同的样本点,则称 A A A与 B B B互不相容。
1.1.6. 事件间的运算
一、事件 A A A与 B B B的并
事件 A A A与 B B B的并是由事件 A A A与 B B B中所有样本点(相同的只计入一次)组成的新事件,或用概率论的语言说,事件 A A A与 B B B中至少有一个发生,即为 A ∪ B A\cup B A∪B.
二、事件 A A A与 B B B的交
事件 A A A与 B B B的交是由事件 A A A与 B B B中公共的样本点组成的新事件,或用概率论的语言说,事件 A A A与 B B B同时发生,即为 A ∩ B A\cap B A∩B.
三、事件 A A A与 B B B的差
事件 A A A与 B B B的差是由在事件 A A A中而不在 B B B中的样本点组成的新事件,或用概率论的语言说,事件 A A A发生而 B B B不发生,即为 A − B A-B A−B.
四、对立事件
事件 A A A的对立事件,即为 A ‾ \overline{A} A,即由在 Ω \Omega Ω中而不在 A A A中的样本点组成的新事件,或用概率论的语言说, A A A不发生,即 A ‾ = Ω − A \overline{A}=\Omega-A A=Ω−A.事件 A A A与 B B B互为对立事件的充要条件是: A ∩ B = ∅ A\cap B=\emptyset A∩B=∅且 A ∪ B = Ω A\cup B=\Omega A∪B=Ω.
五、事件的运算性质
1.交换律
A ∪ B = B ∪ A , A B = B A A\cup B=B\cup A,\quad AB=BA A∪B=B∪A,AB=BA
2.结合律
( A ∪ B ) ∪ C = A ∪ ( B ∪ C ) (A\cup B)\cup C=A\cup (B\cup C) (A∪B)∪C=A∪(B∪C)
( A B ) C = A ( B C ) (AB)C=A(BC) (AB)C=A(BC)
3.分配律
( A ∪ B ) ∩ C = A C ∪ B C (A\cup B)\cap C=AC\cup BC (A∪B)∩C=AC∪BC
( A ∩ B ) ∪ C = ( A ∪ C ) ∩ ( B ∪ C ) (A\cap B)\cup C=(A\cup C)\cap (B\cup C) (A∩B)∪C=(A∪C)∩(B∪C)
4.对偶律(德摩根公式)
A ∪ B ‾ = A ‾ ∩ B ‾ \overline{A\cup B}=\overline{A}\cap \overline{B} A∪B=A∩B
A ∩ B ‾ = A ‾ ∪ B ‾ \overline{A\cap B}=\overline{A}\cup \overline{B} A∩B=A∪B
六、事件域
定义: 设 Ω \Omega Ω为一个样本空间, F \mathscr{F} F为 Ω \Omega Ω的某些子集组成的集合类。如果 F \mathscr{F} F满足:
- Ω ∈ F \Omega\in \mathscr{F} Ω∈F,
- 若 A ∈ F A\in \mathscr{F} A∈F,则对立事件 A ‾ ∈ F \overline{A}\in\mathscr{F} A∈F,
- 若 A n ∈ F , n = 1 , 2 , ⋯ A_n\in\mathscr{F},n=1,2,\cdots An∈F,n=1,2,⋯,则可列并 ∪ n = 1 ∞ A n ∈ F \cup_{n=1}^{\infty}A_n\in\mathscr{F} ∪n=1∞An∈F.
则称 F \mathscr{F} F为一个事件域,又称为 σ \sigma σ域或 σ \sigma σ代数。
1.2. 概率的定义及其确定方法
1.2.1. 概率的公理化定义
定义: 设 Ω \Omega Ω为一个样本空间, F \mathscr{F} F为 Ω \Omega Ω的某些子集组成的一个事件域。如果对任一事件 A ∈ F A\in \mathscr{F} A∈F,定义在 F \mathscr{F} F上的一个实值函数 P ( A ) P(A) P(A)满足:
(1) 非负性公理 若 A ∈ F A\in\mathscr{F} A∈F,则 P ( A ) ≥ 0 P(A)\geq 0 P(A)≥0,
(2) 正则性公理 P ( Ω ) = 1 P(\Omega)=1 P(Ω)=1,
(3) 可列可加性公理 若 A 1 , A 2 , A 3 , ⋯ , A n , ⋯ A_1,A_2,A_3,\cdots,A_n,\cdots A1,A2,A3,⋯,An,⋯互不相容,则
P ( ⋃ i = 1 ∞ A i ) = ∑ i = 1 ∞ P ( A i ) P(\bigcup_{i=1}^{\infty}A_i)=\sum_{i=1}^{\infty}P(A_i) P(i=1⋃∞Ai)=i=1∑∞P(Ai)
则称 P ( A ) P(A) P(A)为事件 A A A的概率,称三元素 ( Ω , F , P ) (\Omega,\mathscr{F},P) (Ω,F,P)为概率空间。
1.2.2. 概率的确定方法
一、频率方法
确定概率的频率方法是在大量重复试验中,用频率的稳定值去获得概率的一种方法,其基本思想是:
(1) 与考察事件 A A A有关的随机现象可大量重复进行。
(2) 在 n n n次重复试验中,即 n ( A ) n(A) n(A)为事件 A A A出现的次数,又称 n ( A ) n(A) n(A)为事件 A A A的频数。称
f n ( A ) = n ( A ) n f_n(A)=\frac{n(A)}{n} fn(A)=nn(A)
为事件 A A A出现的频率。
(3) 人们的长期实践表明:随着试验重复次数 n n n的增加,频率 f n ( A ) f_n(A) fn(A)会稳定在某一常数 a a a附近,我们称这个常数为频率的稳定值。这个频率的稳定值就是我们所求的概率。
二、古典方法
排列的定义: 从 n n n个不同元素中,任取 m m m( m ≤ n m\leq n m≤n, m m m与 n n n均为自然数,下同)个元素按照一定的顺序排成一列,叫做从 n n n个不同元素中取出 m m m个元素的一个排列;从 n n n个不同元素中取出 m m m( m ≤ n m\leq n m≤n)个元素的所有排列的个数,叫做从 n n n个不同元素中取出 m m m个元素的排列数,用符号 A n m A_n^m Anm表示,计算公式为
A n m = n ⋅ ( n − 1 ) ⋅ ( n − 2 ) ⋯ ( n − m + 1 ) = n ! ( n − m ) ! A_n^m=n\cdot(n-1)\cdot(n-2)\cdots(n-m+1)=\frac{n!}{(n-m)!} Anm=n⋅(n−1)⋅(n−2)⋯(n−m+1)=(n−m)!n!
组合的定义: 从 n n n个不同元素中,任取 m m m( m ≤ n m\leq n m≤n)个元素并成一组,叫做从 n n n个不同元素中取出 m m m个元素的一个组合;从 n n n个不同元素中取出 m m m( m ≤ n m\leq n m≤n)个元素的所有组合的个数,叫做从 n n n个不同元素中取出 m m m个元素的组合数。用符号$ C_n^m$表示,计算公式为
C n m = A n m m ! = n ! m ! ( n − m ) ! C_n^m=\frac{A_n^m}{m!}=\frac{n!}{m!(n-m)!} Cnm=m!Anm=m!(n−m)!n!
排列与组合都是计算“从 n n n个元素中任取 r r r个元素”的取法总数公式,其主要区别在于:如果不讲究取出元素间的次序,则用组合公式,否则用排列公式。排列与组合公式的推导都基于如下两条计数原理:
(1) 乘法原理 如果某件事需要经 k k k个步骤才能完成,做第一步有 m 1 m_1 m1种方法,做第二步有 m 2 m_2 m2种方法,……,做第 k k k步有 m k m_k mk种方法,那么完成这件事共有 m 1 × m 2 × ⋯ × m k m_1\times m_2\times\cdots\times m_k m1×m2×⋯×mk种方法。
(2) 加法原理 如果某件事可由 k k k类不同途径之一去完成,在第一类途径中有 m 1 m_1 m1种方法,在第二类途径中有 m 2 m_2 m2种完成方法,……,在第 k k k类途径中有 m k m_k mk种完成方法,那么完成这件事共有 m 1 + m 2 + ⋯ + m k m_1+m_2+\cdots+m_k m1+m2+⋯+mk种方法。
古典方法的思想如下:
- 所涉及的随机现象只有有限个样本点,譬如为 n n n个。
- 每个样本点发生的可能性相等。
- 若事件 A A A含有 k k k个样本点,则事件 A A A的概率为
P ( A ) = 事件 A 所含样本点个数 Ω 中所有样本点的个数 = k n P(A)=\frac{\text{事件}A\text{所含样本点个数}}{\Omega\text{中所有样本点的个数}}=\frac{k}{n} P(A)=Ω中所有样本点的个数事件A所含样本点个数=nk
三、几何方法
确定概率的几何方法的基本思想是:
- 如果一个随机现象的样本空间 Ω \Omega Ω充满整个区域,取度量大小可用 S Ω S_{\Omega} SΩ表示。
- 任意一点落在度量相同的子区域内是等可能的。
- 若事件 A A A为 Ω \Omega Ω中的某个子区域,且其度量大小可用 S A S_A SA表示,则事件 A A A的概率为
P ( A ) = S A S Ω P(A)=\frac{S_A}{S_{\Omega}} P(A)=SΩSA
四、主观方法
统计界的贝叶斯学派认为:一个事件的概率是人们根据经验对该事件发生的可能性所给出的个人信念,这样给出的概率称为主观概率。
1.3. 概率的性质
性质1: P ( ∅ ) = 0 P(\emptyset)=0 P(∅)=0
性质2:(有限可加性) 若有限个事件 A 1 , A 2 , ⋯ , A n A_1,A_2,\cdots,A_n A1,A2,⋯,An互不相容,则有
P ( ⋃ i = 1 ∞ A i ) = ∑ i = 1 ∞ P ( A i ) P(\bigcup_{i=1}^{\infty}A_i)=\sum_{i=1}^{\infty}P(A_i) P(i=1⋃∞Ai)=i=1∑∞P(Ai)
性质3: 对任意事件 A A A,有
P ( A ‾ ) = 1 − P ( A ) P(\overline{A})=1-P(A) P(A)=1−P(A)
性质4: 若 B ⊂ A B\subset A B⊂A,则
P ( A − B ) = P ( A ) − P ( B ) P(A-B)=P(A)-P(B) P(A−B)=P(A)−P(B)
性质5:(单调性) 若 B ⊂ A B\subset A B⊂A,则 P ( A ) ≥ P ( B ) P(A)\geq P(B) P(A)≥P(B)
性质6: 对任意两个事件 A , B A,B A,B,有
P ( A − B ) = P ( A ) − P ( A B ) P(A-B)=P(A)-P(AB) P(A−B)=P(A)−P(AB)
性质7:(加法公式) 对任意两个事件 A , B A,B A,B,有
P ( A ∪ B ) = P ( A ) + P ( B ) − P ( A B ) P(A\cup B)=P(A)+P(B)-P(AB) P(A∪B)=P(A)+P(B)−P(AB)
对任意 n n n个事件 A 1 , A 2 , ⋯ , A n A_1,A_2,\cdots,A_n A1,A2,⋯,An,有
P ( ⋃ i = 1 n A i ) = ∑ i = 1 n P ( A i ) − ∑ 1 ≤ i < j ≤ n P ( A i A j ) + ∑ 1 ≤ i < j < k ≤ n P ( A i A j A k ) + ⋯ + ( − 1 ) n − 1 P ( A 1 A 2 ⋯ A n ) P(\bigcup_{i=1}^{n}A_i)=\sum_{i=1}^{n}P(A_i)-\sum_{1\leq i<j\leq n}P(A_iA_j)+\sum_{1\leq i<j<k\leq n}P(A_iA_jA_k)+\cdots+(-1)^{n-1}P(A_1A_2\cdots A_n) P(i=1⋃nAi)=i=1∑nP(Ai)−1≤i<j≤n∑P(AiAj)+1≤i<j<k≤n∑P(AiAjAk)+⋯+(−1)n−1P(A1A2⋯An)
1.4. 条件概率
1.4.1. 条件概率的定义
所谓条件概率,它是指某事件 B B B发生的条件下,求另一事件 A A A发生的概率,记为 P ( A ∣ B ) P(A|B) P(A∣B),它与 P ( A ) P(A) P(A)是不同的两类概率。
定义: 设 A A A和 B B B是样本空间 Ω \Omega Ω中两事件,若 P ( B ) > 0 P(B)>0 P(B)>0,则称
P ( A ∣ B ) = P ( A B ) P ( B ) P(A|B)=\frac{P(AB)}{P(B)} P(A∣B)=P(B)P(AB)
为**“在 B B B发生下 A A A的条件概率”,简称为条件概率**。
性质: 条件概率是概率,即若设 P ( B ) > 0 P(B)>0 P(B)>0,则
(1) P ( A ∣ B ) ≥ 0 , A ∈ F P(A|B)\geq 0,A\in\mathscr{F} P(A∣B)≥0,A∈F.
(2) P ( Ω ∣ B ) = 1 P(\Omega|B)=1 P(Ω∣B)=1.
(1) 若 F \mathscr{F} F中的 A 1 , A 2 , ⋯ , A n , ⋯ A_1,A_2,\cdots,A_n,\cdots A1,A2,⋯,An,⋯互不相容,则
P ( ⋃ n = 1 ∞ A n ∣ B ) = ∑ n = 1 ∞ P ( A n ∣ B ) . P(\bigcup_{n=1}^{\infty}A_n|B)=\sum_{n=1}^{\infty}P(A_n|B). P(n=1⋃∞An∣B)=n=1∑∞P(An∣B).
1.4.2. 乘法公式
性质:
(1) 若 P ( B ) > 0 P(B)>0 P(B)>0,则
P ( A B ) = P ( B ) P ( A ∣ B ) P(AB)=P(B)P(A|B) P(AB)=P(B)P(A∣B)
(2) 若 P ( A 1 A 2 ⋯ A n ) > 0 P(A_1A_2\cdots A_n)>0 P(A1A2⋯An)>0,则
P ( A 1 A 2 ⋯ A n ) = P ( A 1 ) P ( A 2 ∣ A 1 ) P ( A 3 ∣ A 1 A 2 ) ⋯ P ( A n ∣ A 1 A 2 ⋯ A n − 1 ) P(A_1A_2\cdots A_n)=P(A_1)P(A_2|A_1)P(A_3|A_1A_2)\cdots P(A_n|A_1A_2\cdots A_{n-1}) P(A1A2⋯An)=P(A1)P(A2∣A1)P(A3∣A1A2)⋯P(An∣A1A2⋯An−1)
1.4.3. 全概率公式
性质: 设 B 1 , B 2 , ⋯ , B n B_1,B_2,\cdots,B_n B1,B2,⋯,Bn为样本空间 Ω \Omega Ω的一个分割,即 B 1 , B 2 , ⋯ , B n B_1,B_2,\cdots,B_n B1,B2,⋯,Bn互不相容,且 ⋃ i = 1 n B i = Ω \bigcup_{i=1}^{n}B_i=\Omega ⋃i=1nBi=Ω,如果 P ( B i ) > 0 , i = 1 , 2 , ⋯ , n P(B_i)>0,i=1,2,\cdots,n P(Bi)>0,i=1,2,⋯,n,则对任一事件 A A A有
P ( A ) = ∑ i = 1 n P ( B i ) P ( A ∣ B i ) P(A)=\sum_{i=1}^{n}P(B_i)P(A|B_i) P(A)=i=1∑nP(Bi)P(A∣Bi)
对于全概率公式,需要注意以下两点:
-
全概率公式的最简单形式 假如 0 < P ( B ) < 1 0<P(B)<1 0<P(B)<1,则
P ( A ) = P ( B ) P ( A ∣ B ) + P ( B ‾ ) P ( A ∣ B ‾ ) P(A)=P(B)P(A|B)+P(\overline{B})P(A|\overline{B}) P(A)=P(B)P(A∣B)+P(B)P(A∣B) -
条件 B 1 , B 2 , ⋯ , B n B_1,B_2,\cdots,B_n B1,B2,⋯,Bn为样本空间 Ω \Omega Ω的一个分割,可改为 B 1 , B 2 , ⋯ , B n B_1,B_2,\cdots,B_n B1,B2,⋯,Bn互不相容,且 A ⊂ ⋃ i = 1 n B i A\subset\bigcup_{i=1}^{n}B_i A⊂⋃i=1nBi.
1.4.4. 贝叶斯公式
性质: 设 B 1 , B 2 , ⋯ , B n B_1,B_2,\cdots,B_n B1,B2,⋯,Bn为样本空间 Ω \Omega Ω的一个分割,即 B 1 , B 2 , ⋯ , B n B_1,B_2,\cdots,B_n B1,B2,⋯,Bn互不相容,且 ⋃ i = 1 n B i = Ω \bigcup_{i=1}^{n}B_i=\Omega ⋃i=1nBi=Ω,如果 P ( A ) > 0 , P ( B i ) > 0 , i = 1 , 2 , ⋯ , n P(A)>0,P(B_i)>0,i=1,2,\cdots,n P(A)>0,P(Bi)>0,i=1,2,⋯,n,则
P ( B i ∣ A ) = P ( A B i ) P ( A ) = P ( B i ) P ( A ∣ B i ) ∑ j = 1 n P ( B j ) P ( A ∣ B j ) P(B_i|A)=\frac{P(AB_i)}{P(A)}=\frac{P(B_i)P(A|B_i)}{\sum_{j=1}^{n}P(B_j)P(A|B_j)} P(Bi∣A)=P(A)P(ABi)=∑j=1nP(Bj)P(A∣Bj)P(Bi)P(A∣Bi)
条件概率的三个公式中,乘法公式是求事件交的概率,全概率公式是求一个复杂事件的概率,而贝叶斯公式是求一个条件概率。
1.5. 独立性
独立性是概率论中又一个重要的概念,利用独立性可以简化概率的计算。
1.5.1. 两个事件的独立性
两个事件之间的独立性是指:一个事件的发生不影响另一事件的发生,从概率的角度看,事件 A A A的条件概率 P ( A ∣ B ) P(A|B) P(A∣B)与无条件概率 P ( A ) P(A) P(A)的差别在于:事件 B B B的发生改变了事件 A A A发生的概率,也即事件 B B B对事件 A A A有某种“影响”。如果事件 A A A与 B B B的发生是互不影响的,则有 P ( A ∣ B ) = P ( A ) P(A|B)=P(A) P(A∣B)=P(A)和 P ( B ∣ A ) = P ( B ) P(B|A)=P(B) P(B∣A)=P(B),他们都等价于
\begin{equation}
\label{eq1}
P(AB)=P(A)P(B)
\end{equation}
定义: 如果公式(\ref{eq1})成立,则称事件 A A A与 B B B相互独立,简称 A A A与 B B B独立。否则称 A A A与 B B B不独立或相依。
性质: 若事件 A A A与 B B B独立,则 A A A与 B ‾ \overline{B} B独立, A ‾ \overline{A} A与 B B B独立, A ‾ \overline{A} A与 B ‾ \overline{B} B独立。
1.5.2. 多个事件的相互独立性
定义: 设有 n n n个事件 A 1 , A 2 , ⋯ , A n A_1,A_2,\cdots,A_n A1,A2,⋯,An,对任意的 1 ≤ i < j < k ⋅ ≤ n 1\leq i<j<k\cdot\leq n 1≤i<j<k⋅≤n,如果以下等式成立
{ P ( A i A j ) = P ( A i ) P ( A j ) , P ( A i A j A k ) = P ( A i ) P ( A j ) P ( A k ) , ⋮ P ( A 1 A 2 ⋯ A n ) = P ( A 1 ) P ( A 2 ) ⋯ P ( A n ) \left\{ \begin{array}{l} P(A_iA_j)=P(A_i)P(A_j),\\ P(A_iA_jA_k)=P(A_i)P(A_j)P(A_k),\\ \vdots\\ P(A_1A_2\cdots A_n)=P(A_1)P(A_2)\cdots P(A_n) \end{array} \right. ⎩⎪⎪⎪⎨⎪⎪⎪⎧P(AiAj)=P(Ai)P(Aj),P(AiAjAk)=P(Ai)P(Aj)P(Ak),⋮P(A1A2⋯An)=P(A1)P(A2)⋯P(An)
则称此 n n n个事件 A 1 , A 2 , ⋯ , A n A_1,A_2,\cdots,A_n A1,A2,⋯,An相互独立。