概率论

0. 前言

本文主要旨在对概率论的基础概念与知识进行概要的总结，以便于使用到时可以参考。
概率论是数理统计的基础，也是很多机器学习模型的支撑，概率论在机器学习中占主要地位，因为概率论为机器学习算法的正确性提供了理论依据。

---

1. 概率论的基本概念

1.1 基本概念

随机实验（E）

（1）可以在相同的条件下重复地进行
（2）每次实验的可能结果不止一个，并且事先明确知道实验的所有可能结果
（3）每次试验将出现哪一个结果无法预知
例子：抛一枚硬币，观察正面，反面出现的情况

样本空间 (Ω)

随机试验所有可能的结果组成的集合

样本点

样本空间的元素，即每个可能的结果

随机事件

随机试验E的样本空间S的子集称为随机事件

基本事件

样本空间的单个元素，一个可能结果构成的集合

必然事件（全集）、不可能事件（空集）

事件的关系与事件的运算 （类似于集合运算）

包含关系、和（并）并事件、积（交）事件、差事件、互不相容（互斥）、逆事件（对立事件）

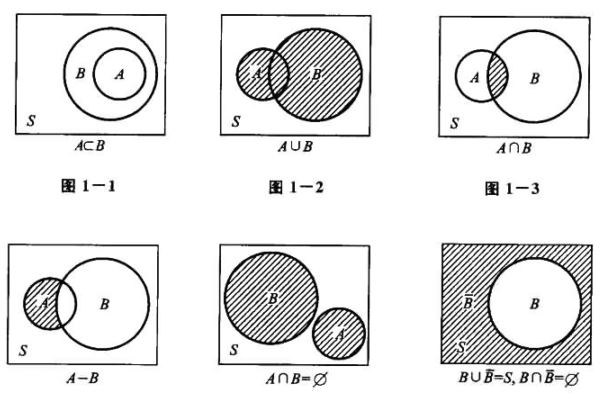
运算规律

1、交换律：
$A\cup B=B\cup A$
$A\cap B=B\cap A$
2、 结合律：
$A\cup (B\cup C)=(A\cup B)\cup C$
$A\cap (B\cap C)=(A\cap B)\cap C$
3、分配律：
$A\cup (B\cap C)=(A\cup B)\cap (A\cup C)$
$A\cap (B\cup C)=(A\cap B)\cup (A\cap C)$
$A\cap (B-C)=(A\cap B)-(A\cap C)$
4、德摩根律（对偶律）：
$\overline{A\cup B}=\overline{A}\cap \overline{B}$
$\overline{A\cap B}=\overline{A}\cup \overline{B}$
常用结论：
$A\overline{A}=\Phi$； $A\cup \overline{A}=\Omega$；
$A\cup B=A+B-AB=(A-B)+(B-A)+AB$

---

1.2 频率与概率

频率

定义：在相同条件下，进行n次试验，在这n次试验中，事件A发生的次数，称为事件A发生的频数，比值：f = 频数／试验次数，称为事件A发生的频率。
基本性质：
（1）0 <= f <= 1 ;
（2）f(Ω) = 1;
（3）两两互不相融事件的可列可加性。
稳定性：当试验重复次数很大时，频率趋于稳定，可以用来表征事件A发生可能性的大小。

概率

定义： 设E是随机试验，样本空间为Ω，对于E的每一个事件A赋予一个实数，记为P(A)，称为A的概率。
性质：
（1）非负性 0 =< P(A) <= 1;
（2）正则性 P(Ω) = 1;
（3）可列可加性 若有互不相容的事件：$A_1,A_2,A_3,...$，
\quad\quad 则 $P(\cup A_j)=\sum P(A_j)$

---

1.3 等可能概型（古典概型）

设E是一个试验，满足：（1）只有有限多个样本点；（2）每个样本点发生的可能性相同（等可能性）。
典型例子：抛硬币
长期实践的发现：“概率很小的事件在一次试验中几乎是不发生”（称之为实际推理原理）

排列
排列：从n个不同元素中，任取m(m ≤ n,m与n均为自然数)个元素按照一定的顺序排成一列，称为从n个不同元素中取出m个元素的一个排列。
排列数：$A_n^m=n(n-1)(n-2)\dots \dots (n-m+1)=\frac{n!}{(n-m)!}$
组合
组合：从n个不同元素中，任取m(m≤n)个元素并成一组，叫做从n个不同元素中取出m个元素的一个组合。
组合数：$C_n^m=\frac{A(n,m)}{m!}$
公式：
$C_n^m=C_n^{n-m}$
$C_n^m+C_n^{m-1}=C_{n+1}^m$
$C_n^0+C_n^1+...+C_n^n=2^n=(1+1{)}^n$

例1：
袋子中有a个黑球，b个白球，先一只只地摸出来，求：第k次摸到黑球的概率（1<= k <= a+b）
解法1：（排列）
思路：
样本空间为a+b个球的全排列，有利场合为第k个球确定为黑球，有a种可能，然后剩下a+b-1个球随机排列。
样本空间：(a+b)!
有利场合：a×(a+b-1)!
故：
$P=\frac{a\times (a+b-1)!}{(a+b)!}=\frac{a}{a+b}$
解法2：（组合）
思路：
样本空间为从a+b个格子中选取a个放置黑球，其余一定放白球，故为$C_{a+b}^a$；有利场合为第k个确定放置黑球，从剩下a+b-1个格子中选取a-1个格子放置剩下的黑球，其余放白球，故为$C_{a+b-1}^{a-1}$。
样本空间：$C_{a+b}^a$
有利场合：$C_{a+b-1}^{a-1}$
故：
$P=\frac{C_{a+b-1}^{a-1}}{C_{a+b}^a}=\frac{a}{a+b}$
PS：这个例子就是抽签模型

例2：
设有n个球，每个都可以以同样的概率$\frac{1}{n}$落到N个格子的每一个格子中（N>=n），求：
（1）某指定的n个格子中各有一个球的概率P(A)；
（2）任何n个格子中各有一个球的概率P(B)；
解：
样本空间：$N^n$
$P(A)=\frac{n!}{N^n}$
$P(A)=\frac{C_N^n\cdot n!}{N^n}=\frac{N!}{N^n\cdot (N-n)!}$
PS：这个模型可用于计算具有相同生日的人的概率

---

1.4 条件概率

（1）条件概率：
设有两个事件A和B，$P(A)̸=0$，在已知A发生的条件下B发生的概率记为：$P(B|A)=\frac{P(AB)}{P(A)}$；满足概率的三个基本性质。
乘法公式：$P(AB)=P(A)P(B|A)$
（2）全概率公式：
设$B1,...,Bi,...,Bn$是$\Omega$的一个划分（完备事件组），$B_1\bigcup B_2\bigcup ...\bigcup B_n=\Omega ,B_i\bigcap B_j=\varnothing ,i̸=j,P(B_i)>0$, 其中 i=1, 2, 3, …，得到：
全概率公式：$P(A)=P(A\Omega )=P(A\bigcap (B_1\bigcup B_2\bigcup ...\bigcup B_n))=P(A{B}_1\bigcup A{B}_2...\bigcup A{B}_n)={\sum }_{i=1}^{n}P(A{B}_i)={\sum }_{i=1}^{n}P(B_i)P(A|B_i)$
PS：把一个要求的事件($\Omega$)分解成若干个互不相容的事件($B_i$)。
（3）贝叶斯公式：
贝叶斯公式：$P(B_i|A)=\frac{P(B_{i}A)}{P(A)}=\frac{P(B_i)P(A|B_i)}{(P(A|B_1)+...+P(A|B_i)+...+P(A|B_n))}=\frac{P(B_i)P(A|B_i)}{{\sum }_{i=1}^{n}P(B_i)P(A|B_i)}$
其中：$P(A)>0,P(B_i)>0$
PS：$P(B_i)$是先验概率，在实际应用中是经验的总结、信息的归纳；
&ThickSpace; \;\quad $P(B_i|A)$是后验概率，表示在事件(A)发生后对各种原因$B_i$发生可能性的分析；

例：
用某检验法诊断肺癌，A：被检验者患有肺癌；B：检验诊断为阳性（患病）；
已知：$P(B|A)=0.95，P(\overline{B}|\overline{A})=0.90，P(A)=0.0004$
求：P(A|B)
解：
$P(A|B)=\frac{P(A)P(B|A)}{P(A)P(B|A)+P(\overline{A})P(B|\overline{A})}=\frac{0.0004\times 0.95}{0.0004\times 0.95+0.9996\times 0.1}=0.0038$

---

1.5 独立性

独立性是概率论和数理统计中很重要的概念，很多情况需要满足独立性才适用，一般根据实践来确定事件之间是否相互独立。
定义：设A、B是随机试验E的两个事件，若 P(AB) = P(A)P(B)， 则称AB事件相互独立，即A和B两个事件的发生互不影响。
定理1：若P(A) > 0 ，且 P(B|A) = P(B) 等价于 AB相互独立
定理2：若A、B相互独立，则其对立事件也相互独立
可以很自然的推广到n个事件的情况

例：
甲、乙两种产品独立生产，甲产品的次品率0.05，乙产品的次品率0.04，现从甲乙产品中各区一件：
（1）两件都是次品的概率P1；
（2）至少有一件是次品的概率P2；
（3）恰好有一件是次品的概率P3。
解：
设A事件为抽取甲为次品，B事件为抽取乙为次品
由于A、B相互独立，故：A，$\overline{A}$；$\overline{A}$，B；$\overline{A}$，$\overline{B}$；相互独立
（1）$P1=P(AB)=P(A)\cdot P(B)=0.05\times 0.04=0.002$
（2）$P2=P(A\bigcup B)=1-P(\overline{A\bigcup B})=1-P(\overline{A}\overline{B})=1-P(\overline{A})P(\overline{B})=1-0.95\times 0.96=0.088$
（3）$P3=P(A\overline{B}\bigcup \overline{A}B)=P(A\overline{B})+P(\overline{A}B)=P(A)P(\overline{B})+P(\overline{A})P(B)=0.86$
PS：独立性和互不相容性
（1）加法公式对应互不相容性；
（2）乘法公式对应独立性；

---

1.6 蒙特霍尔三门问题

游戏规则：

• 参赛者会看见三扇关闭的门，其中一扇的后面有一辆汽车，选中后面有车的那扇门就可以赢得该汽车，另两扇门后则各藏有一只山羊。
• 当参赛者选定了一扇门，但未去开启它的时候，知道门后情形的节目主持人会开启剩下两扇门的其中一扇，露出其中一只山羊。
• 主持人其后会问参赛者要不要换另一扇仍然关上的门。

概率求解（python实现）：

import randomdef MontyHall(Dselect, Dchange):Dcar = random.randint(1,3)if Dselect == Dcar and Dchange == 0:return 1elif Dselect == Dcar and Dchange == 1:return 0elif Dselect != Dcar and Dchange == 0:return 0else:return 1# 不确定是否改变选择
def test1(N):win = 0for i in range(N):Dselect = random.randint(1,3)Dchange = random.randint(0,1)win = win + MontyHall(Dselect, Dchange)print(float(win)/float(N))# 确定不改变选择
def test2(N):win = 0for i in range(N):Dselect = random.randint(1,3)Dchange = 0win = win + MontyHall(Dselect, Dchange)print(float(win)/float(N))# 确定改变选择
def test3(N):win = 0for i in range(N):Dselect = random.randint(1,3)Dchange = 1win = win + MontyHall(Dselect, Dchange)print(float(win)/float(N))N = 10000
print("不确定是否改变选择概率：")
test1(N)
print("确定不改变选择概率：")
test2(N)
print("确定改变选择概率：")
test3(N)

运行结果：

不确定是否改变选择概率：
0.4939
确定不改变选择概率：
0.3307
确定改变选择概率：
0.6618

---

1.7 蒙特卡罗方法

• 蒙特卡罗方法，或称计算机随机模拟方法，是一种基于“随机数”的计算方法。
• 使用随机数（通常是伪随机数）来解决计算问题的方法。
• 蒙特卡罗方法在金融工程学，宏观经济学，计算物理学等领域应用广泛。

# 计算$\pi$的蒙特卡洛方法
import randomn=1000000
k=0
for i in range(n):x=random. uniform(-1,1)y=random. uniform(-1,1)if x**2+y**2<1:k=k+1
print(4* float(k)/float(n))

运行结果：

3.142032