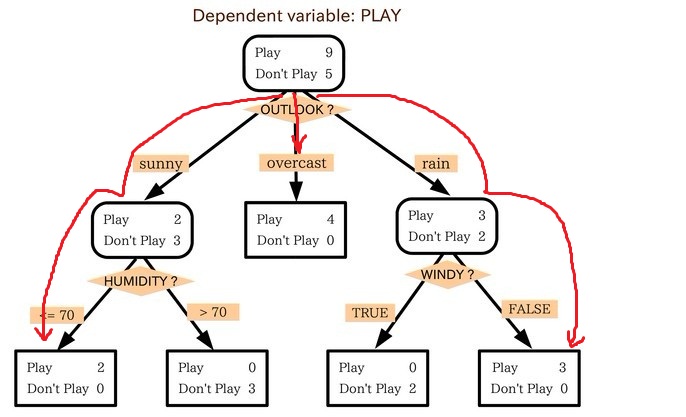
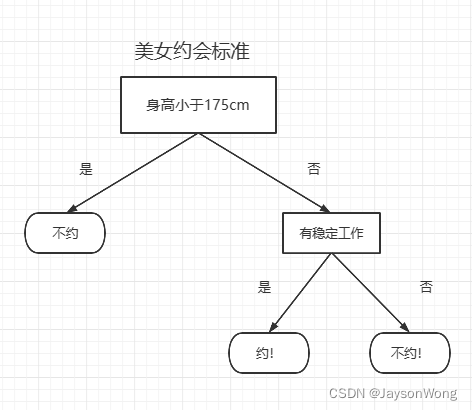
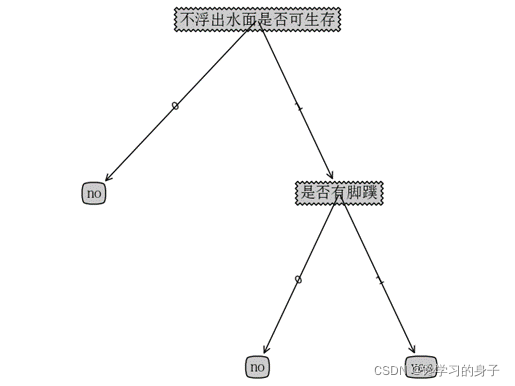
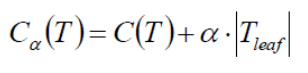概念：

• 是一种树形结构，本质是一颗由多个判断节点组成的树
• 其中每个内部节点表示一个属性上的判断，
• 每个分支代表一个判断结果的输出，
• 最后每个叶节点代表一种分类结果。

通过分析可知：

• 决策树是非参数学习算法
• 决策树可以解决分类问题
• 决策树天然可以解决多分类问题
• 决策树可以解决回归问题：落在叶子节点(对应图中的A、B、C三点)的数据的平均值作为回归的结果
• 决策树可以应用于信用卡评级的案例中,生成相应的分类规则。

1、熵

• 定义

  • 熵在信息论中代表随机变量不确定度的度量。
  • 熵越大，数据的不确定性度越高
  • 熵越小，数据的不确定性越低

• 公式

  H=−∑i=1kpilog⁡(pi)

  • 例子1：假如有三个类别，分别占比为：{1/3,1/3,1/3}，信息熵计算结果为：

    H=−13log⁡(13)−13log⁡(13)−13log⁡(13)=1.0986

  • 例子2：假如有三个类别，分别占比为：{1/10,2/10,7/10}，信息熵计算结果为：

    H=−110log⁡(110)−210log⁡(210)−710log⁡(710)=0.8018

    熵越大，表示整个系统不确定性越大，越随机，反之确定性越强。

  • 例子3：假如有三个类别，分别占比为：{1,0,0}，信息熵计算结果为：

    H=−1log⁡(1)=0

• 公式的转换

  当数据类别只有两类的情况下，公式可以做如下转换   

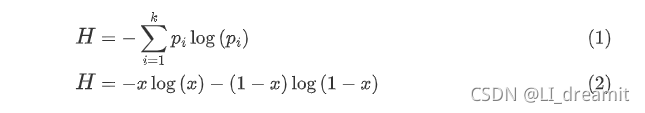
• 代码角度理解信息熵的概念

• import numpy as np
  import matplotlib.pyplot as pltdef entropy(p):return -p*np.log(p)-(1-p)*np.log(1-p)x = np.linspace(0.01,0.99,200)
  plt.plot(x,entropy(x))
  plt.show()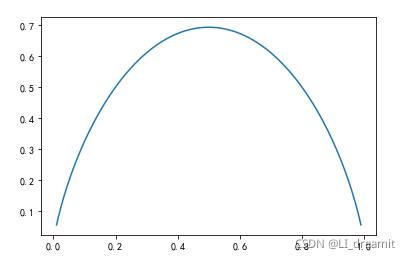

  

2、信息增益 

 

3、信息增益比 

 4、决策树生成-ID3算法&C4.5算法

• ID3算法缺点

  • ID3算法不能处理具有连续值的属性
  • ID3算法不能处理属性具有缺失值的样本
  • 算法会生成很深的树，容易产生过拟合现象
  • 算法一般会优先选择有较多属性值的特征，因为属性值多的特征会有相对较大的信息增益，但这里的属性并不一定是最优的

• C4.5算法的核心思想是ID3算法，对ID3算法进行了相应的改进。

  • C4.5使用的是信息增益比来选择特征，克服了ID3的不足。
  • 可以处理离散型描述属性，也可以处理连续数值型属性
  • 能处理不完整数据

• C4.5算法优缺点

  • 优点：分类规则利于理解，准确率高

  • 缺点

    • 在构造过程中，需要对数据集进行多次的顺序扫描和排序，导致算法的低效
    • C4.5只适合于能够驻留内存的数据集，当数据集非常大时，程序无法运行

• 无论是ID3还是C4.5最好在小数据集上使用，当特征取值很多时最好使用C4.5算法。

5、决策树剪枝

 5.1 为何要进行树的剪枝？

决策树是充分考虑了所有的数据点而生成的复杂树，有可能出现过拟合的情况，决策树越复杂，过拟合的程度会越高。

考虑极端的情况：如果我们令所有的叶子节点都只含有一个数据点，那么我们能够保证所有的训练数据都能准确分类，但是很有可能得到高的预测误差，原因是将训练数据中所有的噪声数据都”准确划分”了，强化了噪声数据的作用。

而剪枝修剪分裂前后分类误差相差不大的子树，能够降低决策树的复杂度，降低过拟合出现的概率。

5.2 剪枝的方法

5.2.1 先剪枝

先剪枝是对决策树停止标准的修改。

在ID3算法中，节点的分割一直到节点中的实例属于同一类别的时候才停止。对于包含较少实例的节点，很有可能被分割为单一实例的节点。为了避免这种情况，我们给出一个阈值，当一个节点分割导致的最大的不纯度下降小于a时，就把该节点看作是叶子结点。该方法选择的阈值对决策树的构建有很大的影响。

（1）当阈值a选择的过大的时候，节点的不纯度依然很高就停止了分裂。此时的树由于生长不足，导致决策树过小，分类的错误率过高。因此需要调整a参数的合理范围之内的值。

（2）当阈值a选择的过小的时候，比如a接近0，节点的分割过程近似于原始的分割过程。

5.2.2 后剪枝

后剪枝是从一个充分生长的树中，按照自低向上的方式修剪掉多余的分支，有两种方法：

（1）用新的叶子结点替换子树，该叶子结点的类标号由子树记录中的多数类决定。

（2）用子树中最常用的分支替代子树。

通常计算前后预期分类错误率，如果修剪导致预期分类错误率变大，则放弃修剪，保留相应的各个分支，否则就将相应的节点分支修剪删除。

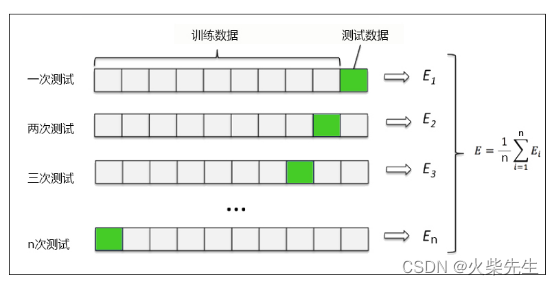
通常采用后剪枝技术是最小的错误剪枝(MEP)技术，即在产生一系列的经过修剪后的决策树候选之后，利用一个独立的测试数据集，对这些经过修剪之后的决策树的分类准确性进行评价，保留下预期分类错误率最小的（修剪后）决策树。

除了最小错误剪枝技术外，还有悲观错误剪枝(MEP)和代价复杂度剪枝(CCP)

6、决策树算法的优缺点

1） 决策树的优点：

直观，便于理解，小规模数据集有效

执行效率高，执行只需要一次构建，可反复使用

（2）决策树的缺点：

处理连续变量不好，较难预测连续字段

类别较多时，错误增加的比较快

对于时间序列数据需要做很多的预处理

可规模性一般

实际分类的时候只能根据一个字段进行

7、构建决策树包括三个步骤:

特征选择：选取有较强分类能力的特征。

决策树生成：典型的算法有ID3和C4.5，它们生成决策树过程相似，ID3是采用信息增益作为特征选择度量，而C4.5采用信息增益比率。

决策树剪枝：剪枝原因是决策树生成算法生成的树对训练数据的预测很准确，但是对于未知数据分类很差，这就产生了过拟合的现象。

8、基尼指数和CART算法

8.1 基尼指数

 8.2 CART算法

 9、决策树经典案例

  9.1Scikit-Learn库实现相亲约会的例子

import pandas as pd
from sklearn.tree import DecisionTreeClassifier# 加载数据集
df = pd.read_csv('data/Sklearntest.csv')
df# 划分数据集
train,test = df.query('is_date!=-1'),df.query('is_date==-1')
# 获取特征值目标值
x_train,y_train = train.drop(['is_date'],axis=1),train['is_date']
x_test = test.drop(['is_date'],axis=1)# 机器学习 参数可选Gini或Entropy
model = DecisionTreeClassifier(criterion='gini')
# 模型训练
model.fit(x_train,y_train)# 预测x_test类别
model.predict(x_test)# 决策树模型可视化
from sklearn.tree import export_graphviz 
from sklearn.externals.six import StringIO
from IPython.display import Image
import pydotplus 
import os# windows 系统添加此行代码,Graphviz路径
# os.environ["PATH"] += os.pathsep + 'C:/Program Files (x86)/Graphviz2.38/bin/'with open("dt.dot", "w") as f:export_graphviz(model, out_file=f)
dot_data = StringIO()
export_graphviz(model, out_file=dot_data,feature_names=x_train.columns,class_names=["is_date:no","is_date:yes"],filled=True, rounded=True)
graph = pydotplus.graph_from_dot_data(dot_data.getvalue()) 
Image(graph.create_png())

9.2 决策树解决泰坦尼克号问题

#1.1导入数据
import  pandas as pd
#1.2.利用pandas的read.csv模块从互联网中收集泰坦尼克号数据集
titanic=pd.read_csv("data/titanic.csv")#2.1首先观察数据的基本特征
titanic.head()#2.2使用pandas的info属性查看数据的统计特征
titanic.info()o
#注：数据共有1313条乘客信息，有些特征是完整的，有一些是不完整的，如name和pclass是完整的，age是不完整的。
#由于数据比较久远，难免会丢失掉一些数据造成数据的不完整，也有数据是没有量化的。
#在决策树模型之前，需要对数据做一些预处理和分析的工作。#2.3特征选择，这里根据对泰坦尼克号的了解，sex，age，pclass作为判断生还的三个主要因素。
X=titanic[['pclass','age','sex']]
y=titanic['survived']
#对当前选择的特征进行探查
X.info()#2.4根据上面的输出，设计几个数据处理的任务
#1）age这个数据列，只有633个，需要补全完整
#2）sex和pclass两个数据列都是类别型的值，需要转化为数值，比如one-hot编码。
#使用平均数或者中位数来填充，对模型偏离程度造成的影响比较小
X['age'].fillna(X['age'].mean(),inplace=True)
X.info()# 数据集的划分
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.25,random_state=33)# 数据集特征转化
from sklearn.feature_extraction import DictVectorizer
vec=DictVectorizer(sparse=False)
#转换特征后，我们发现凡是类别型的值的特征都单独剥离出来了，独成一列特征，数据型不改变其值。
X_train=vec.fit_transform(X_train.to_dict(orient='records'))X_train
vec.feature_names_X_test=vec.transform(X_test.to_dict(orient='records'))# 使用决策树模型预测
from sklearn.tree import DecisionTreeClassifier
#使用默认的配置初始化决策树模型
dtc=DecisionTreeClassifier()
#使用分割的数据进行模型的学习
dtc.fit(X_train,y_train)
#用训练好的模型来对测试数据集进行预测
y_predict=dtc.predict(X_test)# 决策树算法评估
from sklearn.metrics import classification_report
#输出预测准确率
dtc.score(X_test,y_test)  #0.8340807174887892
#输出更加详细的分类性能
print(classification_report(y_predict,y_test,target_names=['died','survived']))