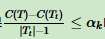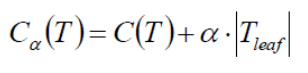决策树

1.1 决策树定义

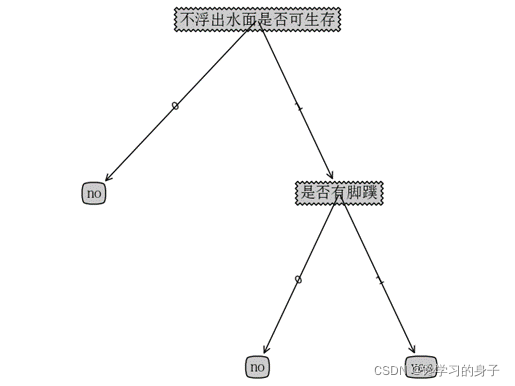
何为决策树，顾名思义，就像树枝状的决策算法，通过各个节点的“决策”，实现对任务的精准分类或回归，决策树常用来处理分类问题，即使你以前没接触过决策树，你也可以通过下图来了解其基本原理：

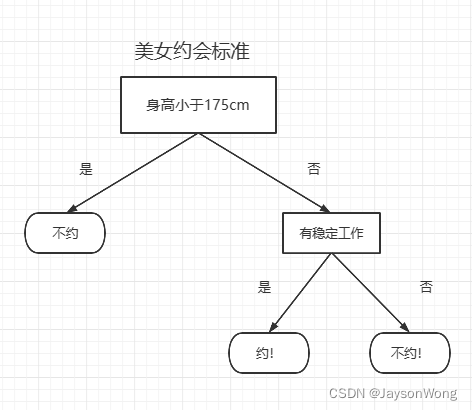
上图就是决策树的决策过程，如果你在某个约会网站上想匹配你心中的那个ta，那你肯定不想在一大群人中很费时的寻找符合你的她，此时，你设想如果有一种算法，能自动的帮你识别哪个美女才是符合你的标准，那该多好啊！通过上图这样一套逻辑，那就能实现是否和美女约会的算法，类似的，这种决策的过程就是决策树的一般思路。

1.2 决策树的基本流程

一般的，一颗决策树包含一个根节点，若干个内部节点和若干个叶节点，叶节点对应决策结果，其他每个节点则对应属性测试，每个节点包含的样本集根据属性测试被划分到子节点中，根节点包含样本全集。决策树遵循的是一种“分而治之”的思维，其一般流程如下：
对于:
训练集D = {（x1,y1), (x2,y2), (x3,y3), …(xm,ym)}
标签集 A = {a1, a2, a3, … am}
过程

• a. 生成节点node
• b. if D 中样本全部属于某一类A， then
• c. 将node标记为A类叶节点， return
• d. end if
• e. 从A中选择最优划分属性ax
• f. for ax 的每一个值 do
• g. 为node生成一个分支
• h. 如果分支为空，则将分支节点标记为叶节点，否则从头开始继续划分
• i. end if
• j. end for

可以看出上面的伪代码显示出决策树的生成是一个递归过程，简单来说就是不停判断数据集中的每个子项是偶属于同一类，如果不属于，则寻找最好的划分方法，然后划分数据集，以此循环，知道所有数据集被划分完毕。

1.3 决策树的划分选择

从1.2得知，决策树的最重要的步骤就是选择最优划分属性！！！因此
最优划分属性有这么几个作用

• 1. 可以大幅减少决策过程，提高决策的准确性
• 2. 可以提高模型的泛化能力，这个可以这么理解，人类识别猫和老鼠的过程，也是决策的过程，人类从动物的叫声、外形、某些局部特征即可分辨，而不是从毛发、脚掌大小、气味、体重、颜色、粪便等等所有特征来决策的，因此，最佳划分属性就好比最容易分辨的特征，能够减少决策提升决策的准确性。

1.3.1 信息增益

信息熵市度量样本纯度最常用的一种指标，其中熵定义为信息的期望值。
信息的定义：如果待分类的事物可能划分在多个分类之中，则符号x的信息定义为：
$$l(x_i)=-lo{g}_{2}p（x_i)$$
其中$p(x_i)$是选择该分类的概率
为了计算熵，我们需要计算所有类别所有可能包含的信息期望值，我们都知道概率相同时期望的公式为：
$$\mu =\sum xf(x)$$
考虑到每种分类的概率可能不同，则信息熵的公式就是把期望公式中的$f(x)$换为信息的定义公式即可，如下：
$$H=-\sum _{i=1}^{n}p(x_i)lo{g}_{2}p(x_i)$$
我们知道，要想训练集D的纯度越高，即第i类样本在x中所占的比例越大，即$p(x_i)$的值越大，即H越小，D越纯 。而
$$信息增益=entroy(前)-entroy(后)$$
前面我们已经得知标签集A有m个可能的分类，若用A来对样本集D来进行划分，则会产生m个分支节点，其中第m个分支节点包含了m中所有在属性A上取值为$a^m$的样本，记为$D^m$，由于每个分支节点中包含的$D^m$不同，因此我们需要赋予其一定的权重，记作$\frac{|D^m|}{|D|}$， 即为信息增益Gain：
$$Gain(D,a)=H(D)-\sum _{m=1}^m\frac{|D^m|}{|D|}H(D^m)$$
因此，信息增益Gain越大，表明用标签集A来划分训练集D所获得的纯度提升越大，如著名的ID3决策树算法就是用信息增益来划分决策节点。

1.3.2 增益率

再次考虑最优划分属性，假如我们给每个样本赋予一个编号，且把编号也假如到决策中，则编号的信息增益最大，若有m个样本，则划分为m类，每个节点仅仅包含一个样本，这样当然其纯度最大，但其没有实际应用价值，因此，C4.5决策树算法不再使用信息增益来划分，而实使用增益率。信息增益如同求最大利润，样本属性越多，其利润自然越大，所以信息增益对取值数数目较多的属性比价友好；而增益率如同求最大利润增长方向，样本属性越少，计算二者的比率就越容易，因此能够在一定程度上克服信息增益的缺陷，对可取值数目较少的属性较友好。其公式为：
$$Gain\_ratio(D,a)=\frac{Gain(D,a)}{SplitInformation(D,a)}$$
其中SplitInformation 等于：
$$SplitInformation(D,a)=-\sum _{m=1}^m\frac{|D^m|}{|D|}lo{g}_2\frac{|D^m|}{|D|}$$

1.3.3 基尼指数

另外一种著名的决策树算法CART使用基尼指数来选择划分属性，基尼指数是指从样本集D中随机抽取两个样本，其类别不一致的概率，其概率越小，纯度越高。其公式为：
$$Gini\_index(D,a)=\sum _{m=1}^m\frac{|D^m|}{|D|}Gini(D^m)$$
其中
$$Gini（D）=\sum _{k=1}^{|y|}\sum _{k\ne k^{‘}}{p}_k{p}_{k^{’}}$$
需要注意的是CART算法永远只生成二叉树，其非叶节点只能为二分类变量，一般为yes or no，其他算法如ID3可以有两个及以上的子节点。

1.4 决策树的优化

1.4.1 剪枝处理

如同现实世界中的树木一样需要定期修剪，以确保其生长方向，美观等，决策树也需要进行“剪枝”来对抗过拟合（Overfitting），我们通过决策树的划分选择得知，决策树有时为了尽可能的正确区分样本，有时会造成分支过多，此时如同把训练集中自身的一些特点都融入一般性质，就如同黑猫是猫，而白猫不是猫一样，十分荒诞。为此决策树需要进行剪枝，一般来说，剪枝的策略有：

• 1. 预剪枝
• 2. 后剪枝

预剪枝：

. 预剪枝是指在决策树生成过程中，对每个节点在划分前先进行评估，如果当前节点的划分不能带来决策树泛化性能的提升，则停止划分并将此节点标记为叶节点。

后剪枝
后剪枝是指先训练一颗决策树，然后自底向上的对非叶节点进行考察，如果将该节点对应的子树替换为叶节点能提升模型的泛化能力，则将该子树替换为叶节点。

1.5 决策树的应用范围

决策树既可以用于分类任务也可以用于回归任务，一般来说，用于分类任务的较多，且不适应环型数据，或圆形数据，对数据的旋转很敏感，具体体现在数据中就是对数据的微小变化敏感，因此在训练过程中尤为要注意，避免过拟合。

1.6 参考资料

• 1. 周志华《机器学习》
• 2. 王静源，贾玮，边蕤 邱俊涛《机器学习实战》
• 3. 李锐，李鹏，曲亚东，王斌《机器学习实战》

下一篇将利用sklearn中的决策树进行实战练习，欢迎查看我的其他博客，点击这查看