文章目录
- Enhancing Recommender Systems With a Stimulus-Evoked Curiosity Mechanism
- 1、引言
- 2、理论基础(原文中使用preliminary)
- 3、问题定义
- 4、本文提出的刺激诱发的好奇心机制(STIMULUS-EVOKED CURIOSITY MECHANISM ,SECM)
- 5、好奇心驱动的推荐框架(CURIOSITY-DRIVE RECOMMENDATION FRAMEWORK,CDRF)
- 6、实验评估
- 7、实验和结果分析
- 8、相关工作
- 9、结论和展望
Enhancing Recommender Systems With a Stimulus-Evoked Curiosity Mechanism
摘要
推荐系统 (RS) 中的经典算法主要强调实现高精度,从而推荐与用户过去选择精确匹配的项目。然而,用户可能会逐渐失去兴趣并渴望一些更鼓舞人心的东西。在心理学中,好奇心是一种批判性的人性,可以有效引导探索行为,因此这种现象可以解释为刺激不足,无法引起对推荐项目的好奇心。受上述启发,这项工作提出了一个好奇心驱动推荐框架 (CdRF),它结合了高度创新的刺激诱发好奇心机制 (SeCM) 以及通过 Borda 计数的基本精度导向算法。在 SeCM 中,我们首先估计每个用户的每个项目上出现的刺激强度,然后使用 Wundt 曲线在计算的强度中建模个性化好奇心。对于目标用户,CdRF 的输出是 N 个相关且高度好奇的项目的排序列表。我们进行了广泛的实验
使用四个公共数据集来评估 SeCM 的每个规范以及整个框架 CdRF 的性能。结果表明,SeCM 可以灵活地生成多样化的项目,而 CdRF 可以增加 ILS、Newness 和 AD 方面的多样性,同时对精度的影响很小。这种研究还提供了一种方法来理解好奇心的个体差异以及好奇心如何在 RS 水平上促进项目探索。
关键词
推荐系统,新奇,冲突,刺激诱发的好奇心机制,相关性偏好,多样性
1、引言
推荐系统 (recommend system,RS) 中的大部分工作采用以准确度为中心的设计,它提供了一个由高度相关的项目组成的候选列表。随着时间的推移,用户可能会感到无聊并且难以专注于当前的活动。 这种普遍现象引发了关于 RS 增强的两个悬而未决的问题:“为什么会发生这种情况?” 以及“如何缓解?”。 从心理学的角度来看,第一个问题可以解释为“没有足够的刺激来引起用户对推送项目的好奇心”。 这种思路鼓励设计额外的好奇心机制,以通过推荐激发好奇心的项目的能力来丰富现有的面向准确性的 RS。 提到的好奇心机制成为对第二个问题的合理缓解,也是我们在本文中关注的问题。
在文献中,只有四项工作专门用于该主题。 Santos从一组志愿者那里收集了 CEI-II 问卷,然后根据这些统计数据计算给定用户的好奇心水平。Santos 工作的一个主要限制是它需要人工干预。除了Santos 的问卷式工作外,Wu等人分别自动为推荐任务建模惊喜驱动的好奇心和不确定性驱动的好奇心。与 Wu 试图最大化推荐项目多样化的工作不同,Zhao等人提出了一种基于好奇心的 RS,称为 CBRS,它利用新奇驱动的好奇心模型来推荐相关但多样化的音乐曲目。但是,如果数据不是 Beta 分布的,则无法处理这种情况,因此严重限制了其大规模应用。此外,CBRS 忽略了这样一个事实,即好奇心通常是由多种因素引起的,而不仅仅是新颖性。其他好奇心模型也存在类似的问题。鉴于以上突出的缺点,因此这项工作旨在设计一个更通用和更全面的好奇心机制。
好奇心研究的一个紧迫挑战是挖掘其根本原因。 幸运的是,好奇心驱动、社会冲突和中级唤醒潜能 (Intermediate Arousal Potential,IAP) 的心理学理论给我们带来了一些启示:1) 多个刺激同时出现在一个项目上,而不是单独出现。 即每个项目对用户呈现一个整体的刺激强度; 2)通常,中等程度的刺激支配着好奇心的唤起; 3) 每个人的好奇心是不一样的。 在这些方面,实际上有两个子任务应该在好奇心机制的层面上考虑。 一是对刺激强度进行定量分析。 二是根据每个用户对这些强度的容忍度来模拟他们的个性化好奇心。 为这些子任务提供解决方案会产生一种新的刺激引发的好奇心机制(Stimulus-evoked Curiosity Mechanism),称为 SeCM。
为了完成推荐,SeCM 被纳入本文提出的好奇心驱动推荐框架(Curiosity-drive Recommendation Framework,CdRF),结合现有的面向准确性的算法 Borda Count 。 因此,CdRF 能够增强 RS 以保持与用户过去的选择可接受的相关性(即,Precision 形式的高精度),同时实现多样性的显着增益(即ILS、Newness 和 AD形式的高度多样性)。 总而言之,我们的主要贡献在于:
- 我们采用心理启发的观点来探索好奇心及其对推荐问题的根本原因的影响。到目前为止,很少有工作认识到好奇心的重要性及其对 RS 的影响,这项研究旨在为这种很少探索的领域做出贡献。
- 我们设计了一种新颖的刺激引起的好奇心机制SeCM。它不仅提供了一种衡量新颖性的方法,而且提供了一种衡量冲突的方法,因为它们都是引起好奇心的关键因素。据我们所知,这是第一次在RS背景下衡量冲突的努力,也是第一次尝试将新颖性研究与好奇心研究的冲突相结合。
- 作为 SeCM 的核心,个性化好奇心使用 Wundt 曲线结合避免无聊 (Avoidance of Boredom,AoB) 和避免焦虑 ( Avoidance of Anxiety,AoA)规则进行建模。具体而言,建模任务被视为基于Saunders对 Wundt 曲线的定义的优化问题。 SeCM为用户输出一系列关于项目的好奇心分数。就我们而言知道,这是第一个创造性地赋予Saunders的Wundt曲线学习能力并将其扩展到 RS 案例的工作。
- 为了获得潜在项目的 Top-N 排名列表,我们提出了一个通用推荐框架CdRF。它通常将面向精度的方法、好奇心机制和排名优化方法结合在一起,以获得更全面的 RS。
- 在两个电影数据集和两个具有十多个竞争对手(规格)的书籍数据集上进行的大量实验验证了 SeCM 和 CdRF在推荐相关和多样化项目方面的有效性。
2、理论基础(原文中使用preliminary)
由于我们研究的跨学科,我们介绍了心理学领域广泛使用并在我们的工作中采用的与好奇心相关的理论和术语。
2.1 好奇心驱动理论
心理学家 Berlyne 将好奇心定义为一种驱动力,它促进探索性行为以更多地了解来源不确定性,主要由新奇和冲突引起,目的是获得足够的知识以减少不确定性。 Berlyne 还提出,好奇心似乎是由一种或一组刺激物引起的,如新奇刺激物、冲突刺激物等,通常有不止一种刺激物并存而不是独立存在。 在本文中,我们主要关注引起好奇心的新奇和冲突刺激的复合物,并利用它来增强 RS 以进行 Top-N 项目推荐。
2.2 社会冲突理论
日常经验表明,决策往往伴随着冲突。 Debra Gerardi 认为冲突可以建立联系并培养好奇心。 Kurt Lewin 是最早将决策和心理冲突的概念结合在一起的人之一。 根据选择的价值,冲突被分类为接近-接近冲突、回避-回避冲突和接近-回避冲突(approach-avoidance conflict,AAC)。 在approach-avoidance conflict的情况下,需要在可取的和不可取的结果之间做出决定。 例如,由于社交同行提供不相容的选择(例如,在较高评分与较低评分共存的情况下),是否观看“侏罗纪公园”电影可以产生AAC。 正如 Lewin 所说,人们经常处于 AAC 状态,本研究的冲突与 AAC 相关。
- 了解AAC
2.3 中级唤醒潜能理论
1870 年代,Wilhelm Wundt 引入了“最佳刺激水平”的概念,并假设刺激水平与快感基调之间存在倒U 关系,即众所周知的“Wundt 曲线”。 它指出,许多形式的刺激水平在中等强度下是令人愉悦的,而在强度过高时变得令人不快。 Berlyne基于冯特的理论,形成了“中级唤醒潜力”(Intermediate arousal potential,IAP)理论。 它表明人们有时会远离对象,有时会接近并检查它们,当唤醒潜力仅略微接近最佳时,实际探索更有可能发生,因此很容易恢复到最佳状态。
为了说明,我们在我们的好奇心驱动推荐任务的背景下介绍了 IAP 过程,如图 1 所示。
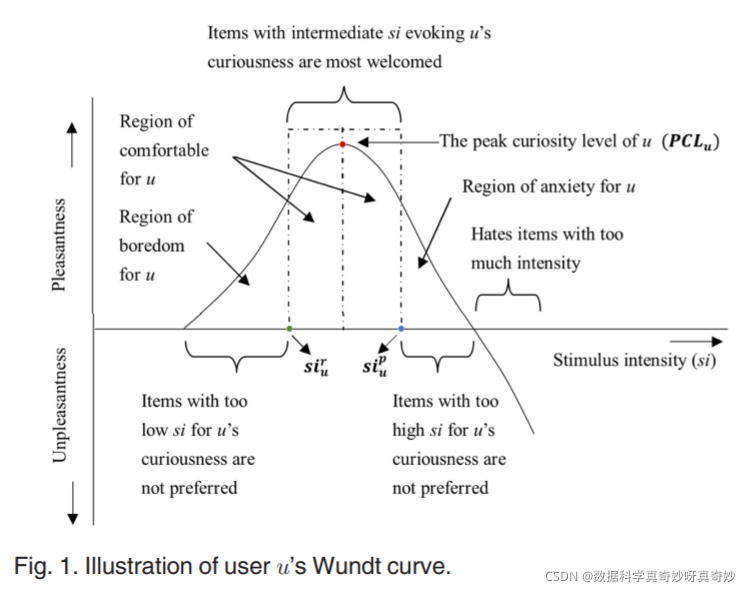
x 轴是指刺激强度 (si),y 轴是指用户 u 的愉快反馈(x 轴上方)或不愉快的反馈(x 轴下方)。我们可以观察到,u 的愉悦度最初会增加,直到达到最高好奇心水平(peak curiosity level ,PCL),而之后si再增加就会减少愉悦度。这种现象可以通过以下事实来解释:用户 u (1) 更喜欢具有中间 si 的物品,从而唤起她的好奇心; (2) 对熟悉或琐碎的项目感到厌烦; (3) 对不可学习或随机的项目感到焦虑; (4) 讨厌 si 太多的物品。总之,Wundt曲线假定个人通常努力保持中等程度的刺激性觉醒,避免无聊和焦虑。因此,光谱有两端:AoB 和 AoA,分别反映刺激选择的规则。 AoB 表示低于某个刺激阈值( s i u r si_u^r siur) 的项目,用户会因缺乏刺激而感到无聊。 AoA 表示,超过某个刺激阈值 ( s i u p si_u^p siup),用户将因压倒性刺激而变得焦虑。这为我们的推荐任务提供了一个新的角度和切入点:对于目标用户 u,最令人愉悦的项目是那些呈现中间刺激的项目;而对于RS,推荐刺激强度在[ s i u r si_u^r siur, s i u p si_u^p siup]范围内的项目更实用。
此外,另一个关键点是刺激反应也必然存在个体差异,因为它们的刺激耐受水平不同。例如,保守用户喜欢刺激程度较低的项目,而激进用户可能喜欢刺激程度相对较高的项目。这也提供了对个性化好奇心建模的要求。
3、问题定义
原始数据被组织为一个个四元组( u , i , r , t u,i,r,t u,i,r,t),表示用户u在时间t对于项目i的得分r。本研究将用户集合定义为 U U U,长度为m,项目集合定义为 I I I,长度为n。
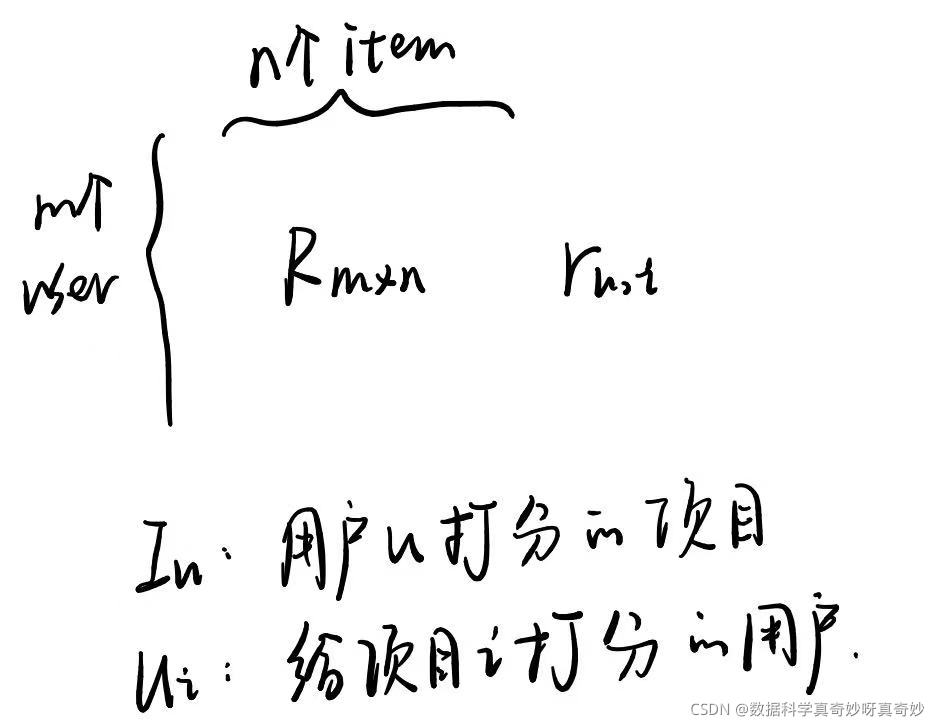
在实际中我们还给每个四元组一个时间戳,因此结合长期连续的的三元组,本文讨论的问题是如何对个体好奇心进行建模,并结合现有的面向精度的 RS 来输出包含 N 个相关但又不同的项目的排名列表。
4、本文提出的刺激诱发的好奇心机制(STIMULUS-EVOKED CURIOSITY MECHANISM ,SECM)
在第 2 节介绍的心理学理论的指导下,我们设计了 SeCM,它限定了整体刺激强度,用 Wundt 曲线对个性化好奇心进行建模,最后为每个用户生成每个项目的好奇心分数。 这些将在接下来的三个小节中描述。
4.1 测量整体刺激强度
Berlyne 确定了几个可能引起好奇心的关键因素:一个是新奇,另一个是冲突。 需要考虑的一个区别是新颖性和冲突之间的区别。 新颖性是一种与用户以前的体验不同的性质,而冲突则是与不相容的反应相关联。 它们分别由新颖刺激强度 s i n o v si^{nov} sinov和冲突刺激强度 s i c o n f si^{conf} siconf量化。 特别是考虑到多个刺激同时出现在一个项目上而不是单独出现,再加上人类更有可能综合权衡所有情况进行决策,因此我们不得不主要关注一个复合刺激案例。 具体来说,我们用 s i u , i si_{u,i} siu,i 表示用户u对项目i出现的整体刺激强度,公式如下,其中α是一个权衡参数。
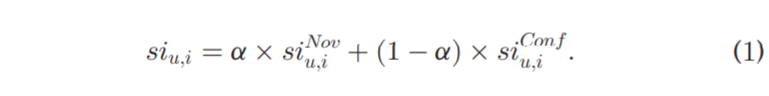
4.1.1 计算新颖刺激强度
Berlyne 假设新颖刺激强度与刺激和先前经验相比的相似程度和最近时间成反比,基于这个标准,本研究提出的公式为:
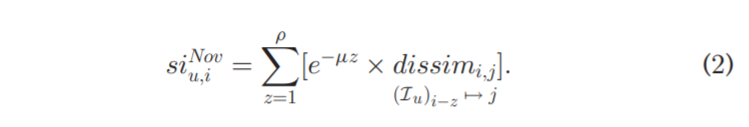
这个公式包含了时间(用μ来确定,时间越长,记忆力越弱)和不相似性(这个项目与用户之前浏览过的项目越不相似,这个项目的新颖性刺激越强)
4.1.2 计算冲突刺激强度
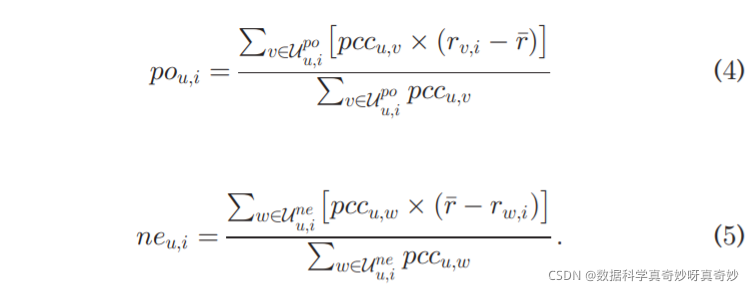
直觉上, p o u , i po_{u,i} pou,i与 n e u , i ne_{u,i} neu,i分别代表用户u的社会同龄人对项目i的积极和消极打分,两者越接近,u 的社会同龄人对 i 的两种反应的不相容性越高,这加强了对 u 冲突的刺激。将冲突刺激强度公式定义为:
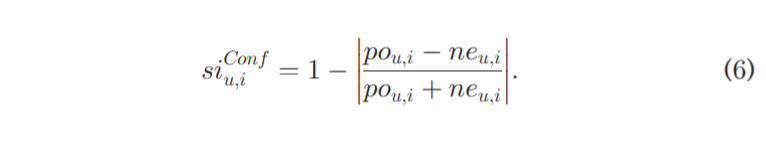
我们可以看到 s i u , i C o n f si^{Conf}_{u,i} siu,iConf在 p o u , i po_{u,i} pou,i与 n e u , i ne_{u,i} neu,i更接近相等时最大程度地提升,这对应于 Berlyne 的冲突刺激标准。
4.2 使用 Wundt 曲线模拟刺激引起的好奇心
考虑到用户的好奇心可以从刺激中唤起,并且通常表现得像一个倒 U 形模式,现在的中心任务是如何使用 Wundt 曲线适当地描绘这种刺激引起的好奇心。 遵循第 2.3 节中提到的 AOB 和 AOA 规则,Saunders 通过两个sigmoid函数的和来近似建模 Wundt 曲线:关于 AoB 的奖励函数和关于 AoA 的惩罚函数。 如图 2 所示,享乐函数 H ( s i ) H(si) H(si) 用于计算实线中给定的享乐值,奖励和惩罚的sigmoid曲线显示为虚线 。

在 Saunders 的工作的基础上,我们用 Wundt 曲线对 u 的好奇心进行建模,通过将原始享乐函数视为用户的预测好奇心函数,用 C ^ u ( s i ) \hat{C}_u(si) C^u(si)表示,该函数计算 u 的预测好奇心分数。 C ^ u \hat{C}_u C^u的域是刺激强度。 按照这个想法, C ^ u ( s i ) \hat{C}_u(si) C^u(si)被定义为奖励函数 R u ( s i ) R_u(si) Ru(si)和惩罚函数 P u ( s i ) P_u(si) Pu(si)的总和。 它们的公式如下:
C ^ u ( s i ) \hat{C}_u(si) C^u(si)= R u ( s i ) R_u(si) Ru(si)+ P u ( s i ) P_u(si) Pu(si)
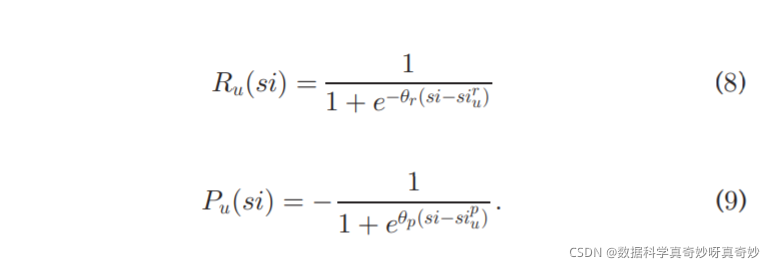
在 (8) 和 (9) 中, s i si si作为指数出现。 θ r \theta_r θr的物理意义是 R u R_u Ru在点( s i u r si_u^r siur, R u ( s i u r ) R_u(si_u^r) Ru(siur))处的斜率, θ p \theta_p θp的物理意义是 P u P_u Pu在点( s i u p si_u^p siup, P u ( s i u p ) P_u(si_u^p) Pu(siup))处的斜率。 如2.3节所述, s i u r si_u^r siur和 s i u p si_u^p siup是两个重要的阈值,分别表示u的最小奖励 s i si si和最小惩罚 s i si si。 请注意,为了简化这项工作,我们直接根据文献18设置 θ r \theta_r θr=20, θ p \theta_p θp=-20,这样就只剩下而 s i u r si_u^r siur和 s i u p si_u^p siup这两个参数。
4.3 估计Wundt 曲线
接下来,我们将估计 Wundt 曲线。 该任务也可以作为优化问题来处理。 具体来说,我们定义了一个损失函数并将其最小化以学习参数 s i u r si_u^r siur和 s i u p si_u^p siup。
给定训练集中的 < u , i , r > <u,i,r> <u,i,r>三元组,我们可以通过公式(1)获得 u 访问的 s i u , i si_{u,i} siu,i 列表。 它由 L u s i L^{si}_u Lusi={ s i u , i si_{u,i} siu,i}表示。让我们对这些强度的分布进行成像,在统计数据中,类似的数据分布可以用直方图进行近似和图形表示。 为了构建直方图,我们将 s i si si([0,1])的整个范围划分为 50 个相等的区间: i t v 0 itv_0 itv0((0,0.02]), i t v 1 itv_1 itv1 ((0.02,0.04]), … ; i t v 4 9 itv_49 itv49(( 0.98,1]), 每一步中的步长 0.02。然后,对于目标用户 u,我们计算每个区间中有多少 s i u , i si_{u,i} siu,i值,通过下面的公式(10)表示:
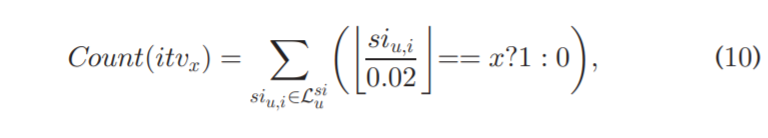
其中 x 是区间的指示符,其值从 0 到 49。 s i u , i 0.02 \frac{si_{u,i}}{0.02} 0.02siu,i值的小数部分由 ⌊ ⌋ \left \lfloor\right \rfloor ⌊⌋运算符四舍五入。 三元运算符(圆括号里面的部分)表示如果条件==条件为真,则返回分号前的值 1,否则返回 0。
第二步,我们引入直方图函数 C u ( s i ) C_u(si) Cu(si)来描述 u 的刺激交互概率。 它正式定义为第 ⌊ s i u , i 0.02 ⌋ \left \lfloor\frac{si_{u,i}}{0.02}\right \rfloor ⌊0.02siu,i⌋个区间的计数值与所有区间的计数值之和的比率。
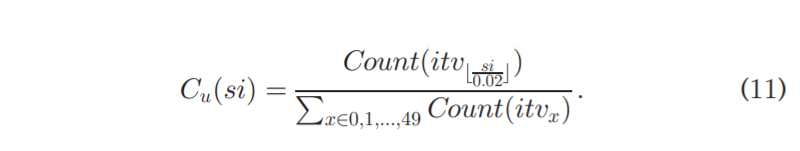
在公式(11)中 C u ( s i ) C_u(si) Cu(si)可以看作是好奇心被唤起的可能性。更具体一点,如果 C u ( s i u , i ) C_u(si_{u,i}) Cu(siu,i)越大,表示更多的 u 访问过的项目的刺激强度出现在[ , ]范围内,所以我们可以假设你对这些项目表现出更多的好奇心,反之亦然。
在这些方面,我们创造性地建议将 C u ( s i ) C_u(si) Cu(si)视为 u 的实际好奇心函数,因为它遵循类似的想法。 这样做的好处是1)它的简单性和为Wundt曲线的学习提供比较直方图的能力; 2)有效利用丰富的交互数据进行好奇心建模。
在我们深入研究成本函数定义之前,我们想举一些例子来方便我们的解释和讨论。
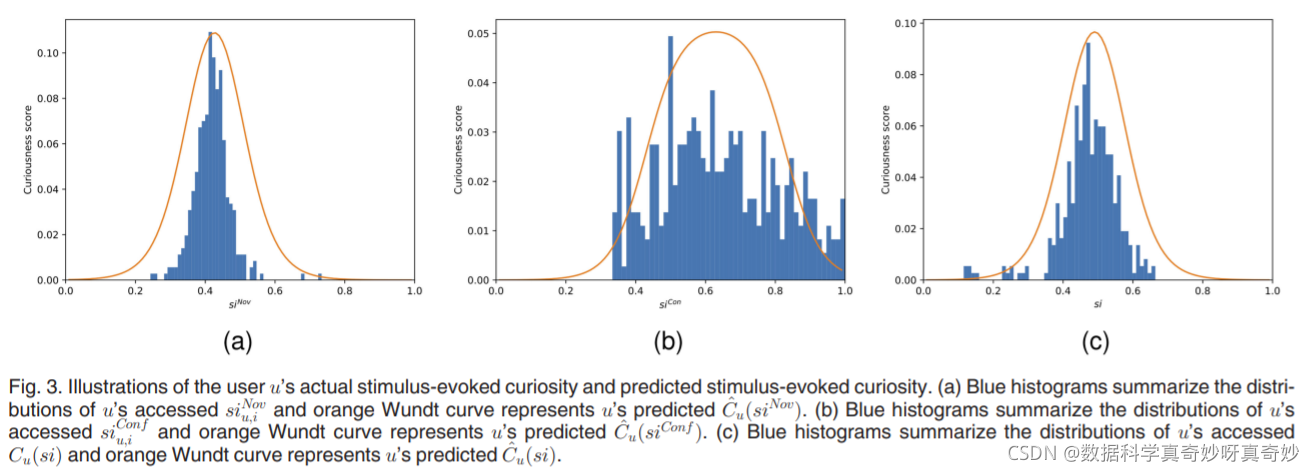
图3,与u有关的三种类型的强度分别展示在三个子图里,u的实际和预测的好奇心强度被整合在一张子图。从所有子图中可以看出,蓝色直方图符合我们的直觉,因为我们预计中间刺激强度对实际探索行为的贡献大于其余区域的贡献。最重要的是,这些观察结果不仅可以为 Wundt 曲线的存在提供实际证据,而且还证实了我们将 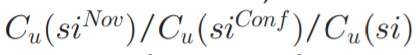
视作u 对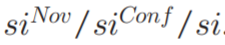
的实际刺激诱发好奇心函数的合理性
在学习过程中,我们使用梯度下降法和最小损失函数 L o s s u Loss_u Lossu来学习获得参数 s i u r si_u^r siur和 s i u p si_u^p siup。
对于每个用户,算法 1 中提供了详细的训练过程。第 1-3 行计算每个间隔的 c o u n t ( ∗ ) count(*) count(∗)值,这需要 O ( 1 ) O(1) O(1)复杂度。 C u ( ∗ ) C_u(*) Cu(∗)值在第 4-6 行中计算。 它的时间复杂度约为 O ( n ‾ ) O(\overline{n}) O(n),其中 n ‾ \overline{n} n是训练集中用户访问的平均项目数。 对于每次迭代,参见第 9-10 行,梯度和更新规则是在两个变量上计算的,因此计算时间为 O ( 1 ) O(1) O(1)。 总时间复杂度为 O ( n ‾ + t ) O(\overline{n}+t) O(n+t),其中 t 是迭代次数。 我们可以看到,为所有用户学习个体的 Wundt 曲线不需要更高的运行时间,因为只需要 O ( m ∗ ( n ‾ + t ) ) O(m*(\overline{n}+t)) O(m∗(n+t))时间复杂度,因为 t 和 n ‾ \overline{n} n通常非常小,因此允许实时应用所提出的好奇心模型。

一旦Wundt曲线被估计出来了,我们就可以把 s i u , i si_{u,i} siu,i代入Wundt曲线来预测用户u对项目i的好奇心,记为 c u r u , i cur_{u,i} curu,i, c u r u , i cur_{u,i} curu,i= C ^ ( s i u , i ) \hat{C}(si_{u,i}) C^(siu,i)
为了强调我们的贡献,值得区分 Saunders 和我们的 Wundt 曲线模型。 Saunders 假设 Wundt 曲线保持不变,不会或不能变化,因为它将 s i u r si_u^r siur和 s i u p si_u^p siup限制为预先给定的常数。然而,这个假设总是不成立。一方面,很难让所有用户提前共享一组固定参数。因为即使面对同样的刺激,不同的人也会伴随着不同的好奇心。另一方面,好奇心不是静态的结果,而是需要不断学习的动态状态。在这些方面,我们创造性地为Saunders 的建模提供了学习能力。通过这样做,我们促进了使用网络规模的交互数据来估计 Wundt 曲线,从而更恰当地描述个人的好奇心。这个想法在很大程度上增强了Saunders 建模的适用性和可行性。其他遵循倒U形Wundt曲线模式的案例,例如房地产价格与消费的关系等,也可以类似地描绘和学习。因此,我们的建模方法表现出高度的灵活性和广阔的潜力。
5、好奇心驱动的推荐框架(CURIOSITY-DRIVE RECOMMENDATION FRAMEWORK,CDRF)
CdRF的整体框架如图4所示。CdRF有两层:数据层和模型层。 一旦建立了用户历史记录,数据层为模型层提供及时有序的训练数据和测试数据。 模型层主要由三个阶段组成。 阶段 1 通过执行现有的面向准确性的方法 (AoM) 计算项目的用户相关性偏好分数(由 r e l u , i rel_{u,i} relu,i表示)。 第 2 阶段通过提议的 SeCM 计算 c u r u , i cur_{u,i} curu,i。 阶段 3 通过 Borda 计数对候选列表进行排序,以在 r e l u , i rel_{u,i} relu,i和 c u r u , i cur_{u,i} curu,i之间取得平衡,最后为目标用户 u 输出占据前 N 个位置的项目。 考虑到第 2 阶段在第 4 节中已详细介绍,在下文中,我们将分别介绍第 1 阶段和第 3 阶段。
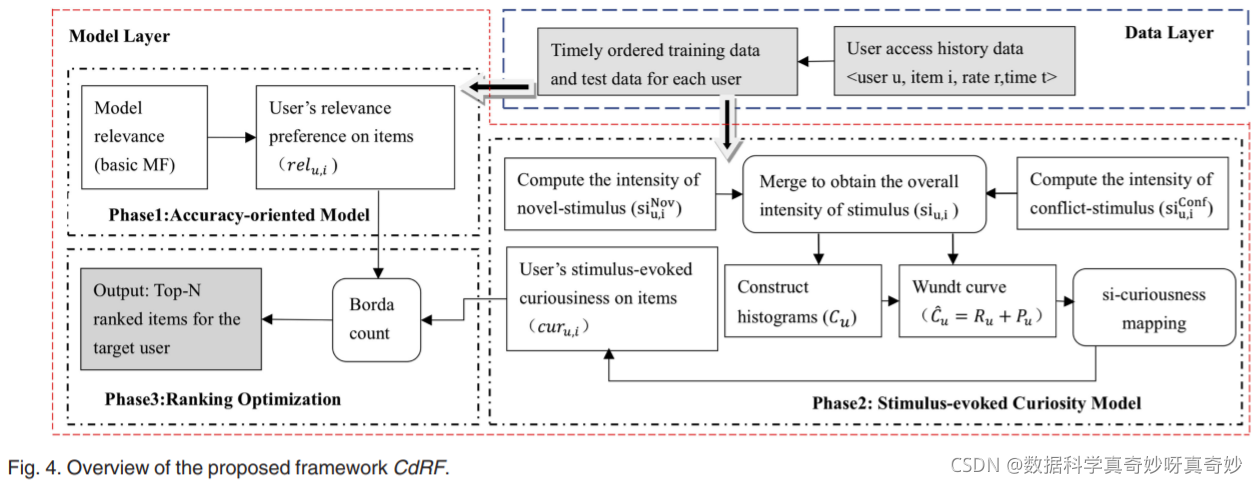
5.1 面向精度的方法(Accuracy-Oriented Method,AOM)
MF模型越来越受欢迎,并被证明在RS中实现了高精度。 为了生成准确的推荐,CdRF 的一个合理选择是IF-MF,因为它是为 Top-N 项目排名量身定制的最成功和使用最广泛的 MF之一。 从技术上讲,让P是一个m*n维矩阵,每个元素由下面的公式计算:
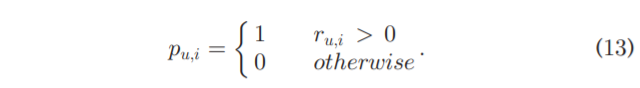
然后用下面的公式表明我们对 用户在项目 i 上的评分的信心,
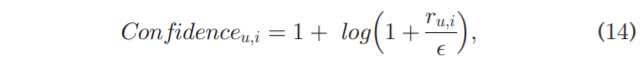
其中, ϵ \epsilon ϵ是一个经过对数缩放的小常数。
后面没怎么看懂,大概意思就是有一个函数,这个函数里隐藏了两个潜在矩阵X和Y,经过反复的学习对这个函数求最小值,得到这两个潜在矩阵。然后
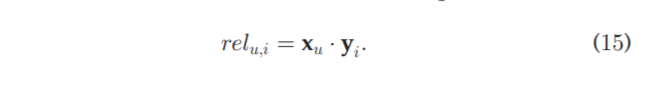
这就是面向精度的方法了。
5.2 排名优化
在最后一个阶段,我们尝试通过排名优化实用程序来平衡用户的好奇心和她对推荐的相关性偏好。 在实践中,我们采用加权 Borda 计数,因为它有利于获得选民广泛共识支持的候选人。 映射到我们的案例,投票者参考两个排名列表:按相关性偏好分数 r e l u , i rel_{u,i} relu,i的降序排序的 L u R L^R_u LuR,以及按好奇心分数 c u r u , i cur_{u,i} curu,i降序排序的 L u C L^C_u LuC。相应地,Borda 计数将 s c o r e u , i R score^R_{u,i} scoreu,iR和 s c o r e u , i C score^C_{u,i} scoreu,iC通过下面的公式与i相连。其中t表示两个列表的长度, ∣ L u R ∣ \lvert {L^R_u}\rvert ∣LuR∣= ∣ L u C ∣ \lvert {L^C_u}\rvert ∣LuC∣=t。pos函数分别表示i在两个列表中的位置。
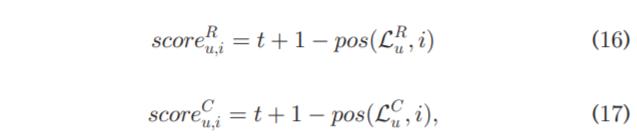
以上都做完了之后就可以计算最终的得分:
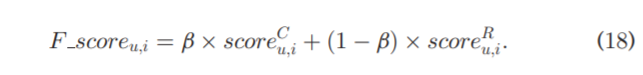
β \beta β是一个权衡参数,表示用户的好奇心和相关性偏好在最终得分里的权重。最终,所提出的 CdRF 为目标用户 u 生成了一个 Top-N 项目列表,该列表按F_score降序排列。
6、实验评估
在本节中,我们将描述实验数据集、评估指标和竞争对手。
6.1 实验数据集和评估指标
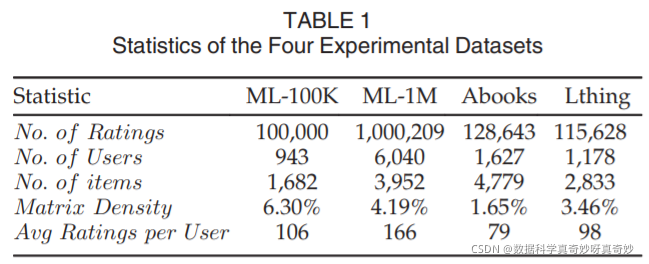
我们对来自 MovieLens-1M 和 MovieLens-100K的两个电影数据集以及来自Amazon Books和 Librarything的两个书籍数据集进行了实验。简而言之,这些数据集缩写为 ML-1M、ML-100K、ABooks 和 Lthing。除了 Lthing 的评分值在 [0.5,5] 范围内,步长为0.5,其他数据集的值在 [1,5] 范围内,步长为1。由于 book 数据集非常稀疏,在我们的实验中,我们按以下顺序对其进行了预处理: 1) 截获时间跨度约为 1.5 年 2) 在 Abooks 上随机选择 10% 的用户 3) 删除评分用户少于 50 的项目; 4) 丢弃对50个以下项目评分的用户。四个数据集的主要统计数据总结在表1中,为了学习Wundt曲线,不可避免地要按照时间顺序对数据进行排序。对于每个用户,前 2/3 (4/5) 个数据用作训练数据,其余 1/3 (1/5) 个用作电影(书籍)数据集上的测试集。我们报告了所有方法 5 次运行的平均结果。
我们提供了两个系列的指标来分别估计这项工作中的准确性和多样性性能。一方面采用 Precision 来评估准确度性能,另一方面采用三个多样性指标(ILS、Newness和 AD)。
ILS是衡量推荐列表多样性的指标,如果推荐列表的物品越不相似, ILS越小, 推荐结果的多样性就越好。
MovieLens 1M数据集:GroupLens Research(http://www.grouplens.org/node/73)采集了一组从20世纪90年末到21世纪初由MovieLens用户提供的电影评分数据。这些数据中包括电影评分、电影元数据(风格类型和年代)以及关于用户的人口统计学数据(年龄、邮编、性别和职业等)。基于机器学习算法的推荐系统一般都会对此类数据感兴趣。含有来自6000名用户对4000部电影的100万条评分数据。它分为三个表:评分、用户信息和电影信息。
MovieLens 100k 电影推荐数据集包含 943个 用户对 1682部 电影的 100000 个 电影的评分(1-5分),数据采集自网站 movielens.umn.edu,时间段为 1997.09-1998.04。下载地址:https://grouplens.org/
LibraryThing(简称Lthing)是一个很受欢迎的书评网站,它允许用户创建一个他们拥有或读过的图书的在线目录。用户可以标记和评分她添加到她的个人图书馆中的所有图书。我们爬取的数据集包含用户对项目的反馈,包括评分和评论。
6.2 竞争对手
我们提供三组竞争对手(共 14 个),从基本竞争对手到 CdRF 组件,以及各种规格的 SeCM。
(1)基本竞争者。 将 CdRF 与基线 IFMF和各种排名竞争对手进行比较,包括 SC [3]、UC [4]、CBRS [5] 和 PopRec。 请注意,SC、UC 和 CdRF 中使用的面向精度的技术是 IF MF,而 SC 采用 R-MF。
(2) CdRF 的组成部分。 为了研究 CdRF 组件的效果,我们提供了两个竞争对手:
- AoM 或 IF-MF。 AoM 发现用户喜欢的相关项目。 该建议可以通过在公式18中设置 Borda 计数权重 β = 0 \beta=0 β=0来消除 SeCM 的影响来实现。 它被指定为 IF-MF,因为我们选择 IF-MF 作为 AoM 的实现。
- SeCM。 它描绘了用户的个性化好奇心。 建议可以通过在公式18中设置 β = 1 \beta=1 β=1来消除 AoM 的影响来执行。
(3)SeCM 的规格。 为了更好地探索 SeCM,我们还比较了 SeCM 的几个规格:
- 复合物。这是我们强烈建议的 SeCM 规范,它考虑了通过 Wundt 曲线了解用户好奇心的复合刺激。如第 4.3 节所述。特别是为了分析Compound内部成分的作用,我们进一步提供了Compound的三个详细规格以供比较。它们是 α \alpha α为0.3、0:5和0.7,分别表示冲突偏差、相等权重和新奇偏差情况。
- Novelty_only。 它仅考虑新颖刺激,通过 Wundt 曲线了解用户的好奇心。 它是通过在公式 (1) 中设置 α = 1 \alpha=1 α=1来实现的。
- Conflict_only。 它仅考虑冲突刺激,通过 Wundt 曲线了解用户的好奇心。 它是通过在公式 (1) 中设置 α = 0 \alpha=0 α=0来实现的。
- Compound_max。 它直接使用复合刺激强度作为好奇心分数。 c u r u , i = s i u , i cur_{u,i}=si_{u,i} curu,i=siu,i
- Novelty_max。 它直接使用新奇刺激强度作为好奇心分数。 c u r u , i = s i u , i N o v cur_{u,i}=si_{u,i}^{Nov} curu,i=siu,iNov。
- Conflict_max。 它直接使用冲突刺激强度作为好奇心分数。 c u r u , i = s i u , i C o n f cur_{u,i}=si_{u,i}^{Conf} curu,i=siu,iConf
7、实验和结果分析
为了验证所提出的 CdRF 及其核心组件 SeCM 的好处,我们在四个数据集上进行了广泛的实验。 我们将 LibRec 库 用于 IF-MF、R-MF 和 PopRec,而其余算法则使用 Python 实现。 所有实验均在一台包含 Intel Xeon CPU E5-2620、2.30 GHz、64 GB RAM、Linux Ubuntu 16.04 操作系统的机器上进行。
7.1 参数设置
反正就是根据文献5设置三个阶段的各种参数
7.2 实验1 估算 SeCM 的规格
第一个系列实验的目的是研究不同 SeCM 规范对推荐性能的影响,并确定每个数据集上 Compound 的最佳组合。具体来说,我们比较1)SeCM中的三个规范:Compound、Novelty_only和Conflict_only; 2)Compound的三个内部规范:conflict_bias、equal_weight和Novelty_bias情况。从技术上讲,我们调整 α \alpha α以获得每个规格。图 5、6、7 和 8 分别展示了四个数据集上四个度量的性能,其中 N 在 β = 1 \beta=1 β=1的情况下取值范围为5 到 30 不等。为了提高可读性,据报道,从明到暗的变化可以增强新颖性,同时减弱冲突(啥呀?)。我们在 ML-1M 数据集上有以下发现:1)在 Precision@N 的形式下,Novelty_bias 始终比其他规范取得显着的性能。 equal_weight 位居第二(图 5a)。这表明新刺激强度和冲突刺激强度的平等处理或更多考虑复合中的新刺激强度可以大大提高 Precision@N。相反,Conflict_only 总体上具有最差的 Precision@N,减少反映了冲突刺激引起的好奇心对准确性的劣势,因为 Conflict_only 主要强调冲突刺激强度; 2)与两种规格的化合物相比,ILS@N 上的 Conflict_only 和 Novelty_only 略有优势(图 5b); 3) 在 Newness@N(图 5c)上,Conflict_only 表现最好,其次是 Novelty_bias; 4) Conflict_only 的 AD@N 性能是最好的,其他的则随着 N 的增加而变化,并且趋向于彼此接近(图 5d)。
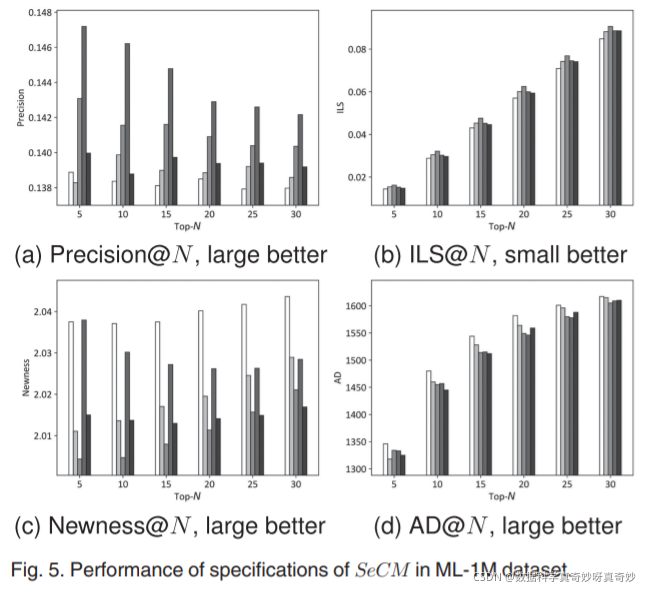
我们还从 ML-100 K 数据集获得了以下观察结果:1)在 Precision@N 的形式中,Novelty_only 和 Conflict_only 都低于 Compound 的所有内部规范(图 6a),表明新颖性和冲突性的平衡刺激与两者中的任何一个相比,可以带来更高的准确性;2)Novelty_biasis 是最引人注目的规范,因为它在所有多样性措施(图 6b、6c 和 6d)上始终保持最佳性能,反映了其优越性和稳定性。
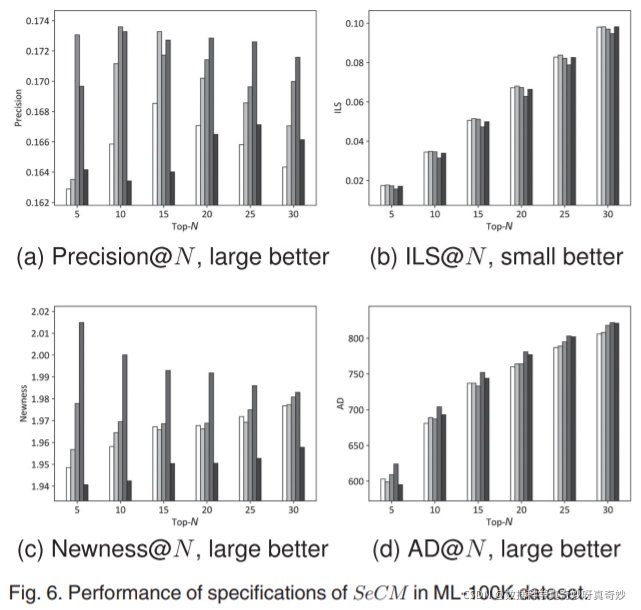
图 7 显示了 ABooks 数据集的结果。 在数据中,我们观察到 1) 对于 Precision@5,conflict_only 达到最佳准确度,其次是 conflict_bias。 然而,随着 N 值的增大,conflict_bias 的性能得到改善,使其能够胜过所有其他规范(图 7a); 2) 在 Newness 上,conflict_bias 明显优于其他规范(图 7c); 3)除了conflict_only之外,随着ILS和AD上N的增长,剩下规范之间的差距越来越小(图7b和7d)。
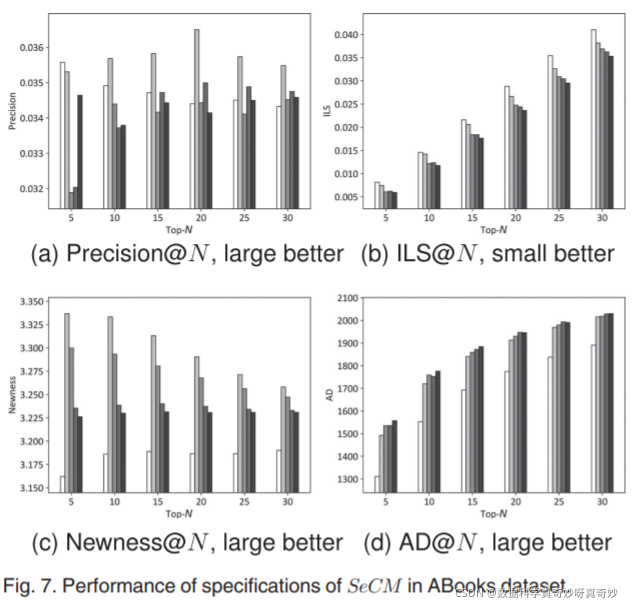
图 8 报告了 Lthing 数据集的结果。 观察到,在precision上(图 8a),三个混合规范总是优于单独模拟冲突刺激引发的好奇心或新奇引发的好奇心的规范(图 8a)。 此外,conflict_bias 实现了最好的 Newness(图 8c)。
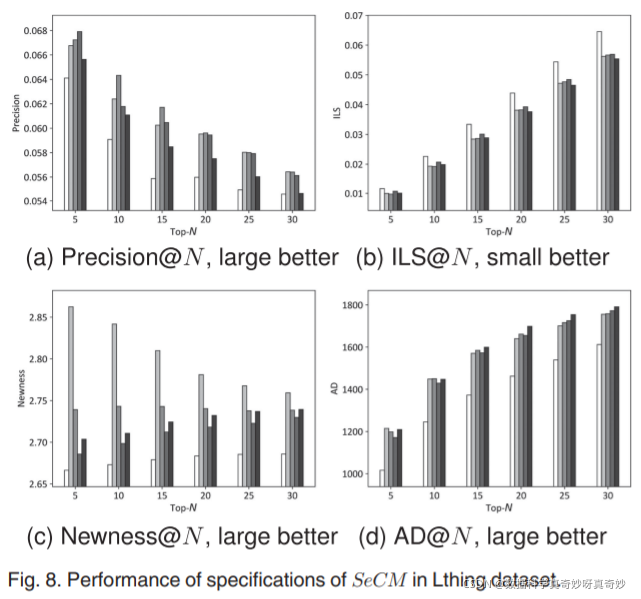
总之,平衡被认为是非常重要的,因为我们可以利用新奇和冲突引起的好奇心。 此外,正如本文前面提到的,用户的好奇心通常取决于一系列因素而不是单个因素。 因此,Compound 更实用。 重要的是,值得一提的是,我们在其余实验中的电影(书籍)数据集上纯粹报告了 α = 0.7 \alpha=0.7 α=0.7 ( α = 0.3 \alpha=0.3 α=0.3) 情况下的 Compound,因为发现在这种情况下Novity_bias (conflict_bias) 成为表现最佳的组合。
7.3 β \beta β对 CdRF 的影响和Wundt 曲线对SeCM的影响
除了调整 Borda 计数权衡 β \beta β以研究好奇心和相关性偏好之间的困境外,第二系列实验主要用于估计推荐性能如何受 Wundt 曲线的影响。 从技术上讲,我们比较了有和没有 Wundt 曲线的 SeCM 的那些规格。 为便于讨论,使用 Wundt 曲线的规格(Compound、Novelty_only 和 Conflict_only)以实线介绍,而没有 Wundt 曲线的“最大”规格(Compound_max、Novelty_max 和 Conflict_max)以虚线介绍。 每一对都涂有相同的颜色和相同的标记,例如。 带三角形的红线用于 Compound 和 Compound_max。 当 N = 5 时,四个数据集的实验结果报告在图 9、10、11 和 12中。

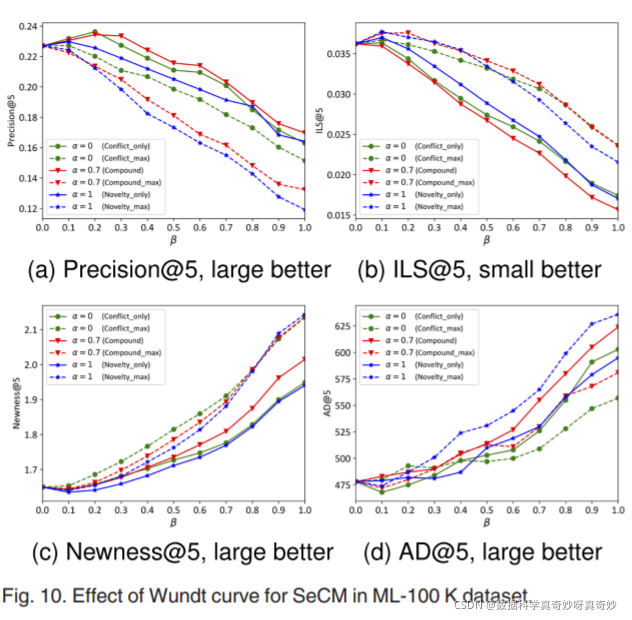
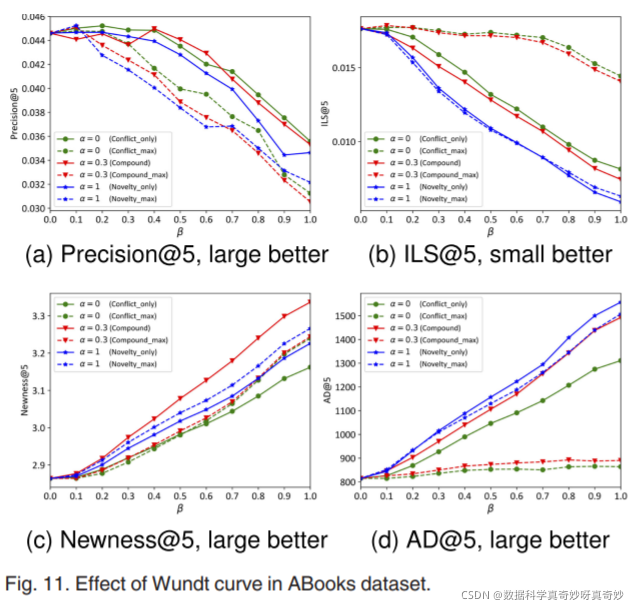

总的来说,当 β \beta β从 0 调整到 1 时,相关性偏好程度会降低。因此,在大多数情况下,随着好奇因素数量在四个数据集上的增加,多样性表现会更好。 这种现象证实了由新奇刺激、冲突刺激或它们的组合引起的好奇心对于让 RS 发现和推荐不同的项目很有价值。 此外,Borda 计数中采用的权衡 β \beta β设法满足相关性偏好、多样性或更有效和灵活的要求。
观察图9a,10a,11a,12a,在 Precision@5 上,实线方法通常优于虚线方法。 我们将此归因于这样一个事实,即 Compound、Novelty_only 和 Conflict_only 通过 Wundt 曲线容纳 AOA 和 AOB 带来更多信息刺激,因此有能力推荐相关和多样化的项目。 而 Compound_max、Novelty_max 和 Conflict_max 遵循单一的 AOB 规则,因此在不考虑相关性偏好的情况下追求高度多样化的项目。 此外,这一现象也证明了利用Wundt 曲线对个人倒U形好奇心进行适应度适应的有效性。
其余子图分别报告了四个数据集上竞争对手之间多样性度量@5 的差异。 在电影数据集上,没有 Wundt 曲线的方法通常比具有 Wundt 曲线的方法可以产生更高程度的多样性,尤其是在 ML1M 上的 AD@5(图 9d)和 ML 上的 Newness@5 的情况下,这并不奇怪 -100K(图 10c)。
然而,在使用 Wundt 曲线的方法上仍然出现了一些亮点。 例如,在 ML-100K 上,Compound、Conflict_only 和 Novelty_only 在 ILS@5 上优于它们的 max 方法(图 10b)。 这可以通过 Wundt 曲线对生成推荐列表的个性化好奇心水平的影响来解释,从而导致更高的 ILS。 在书籍数据集上,上述情况有些不同。 首先,Compound 在 Newness 上优于其他方法,包括没有 Wundt 曲线的方法(见图 11c); 其次,Conflict_max 和 Compound_max 在 ILS 和 AD 上的表现最差(图 11b 和 11d)。 这些表明多样性通常随着 Wundt 曲线而得到改善。
从以上结果,我们得出结论,复合是最有效的方法,因为它保持了出色的精密度,同时提供了相对令人满意的多样性。 这些也表明,Wundt 曲线同时考虑新奇刺激和冲突刺激超过了单独的两者。
为了深入了解来自 IAP 理论的 Wundt 曲线,我们接下来研究基于刺激强度的模拟 Wundt 曲线,无论是单独 (siNov, siConf ) 还是相互结合 (si) 出于好奇。 因此,图 13 中描绘了三个图,其中我们展示了三个真实的插图。 用户 u 是第 10 个用户,用户 v 是 ML-1M 数据集中列出的第 3979 个用户。 u 和 v 在训练集中评分的项目数分别为 267 和 64。 由 C^uð Þ 和 C^vð Þ 分别定义的 u(橙色曲线)和 v(黑色曲线)的估计 Wundt 曲线被合并到相同的图中。 从图中,我们可以得出以下几点:
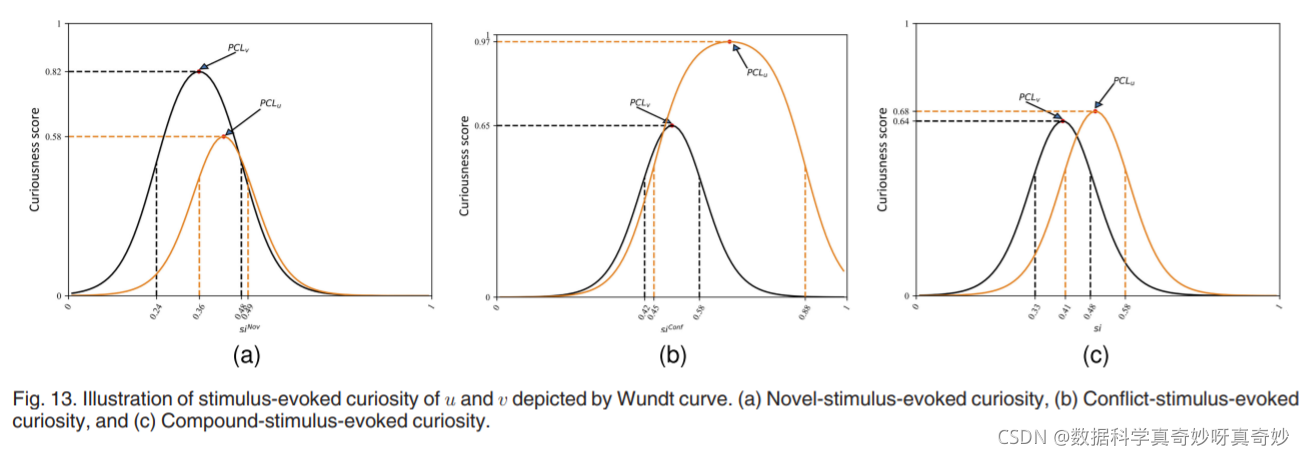
首先,好奇心程度因用户而异。 例如,u 和 v 仅将自己暴露于小说刺激下(图 13a),他们的小说刺激引起的好奇心分别被建模为 C ^ u ( s i N o o v ) \hat{C}_u(si^{Noov}) C^u(siNoov)和 C ^ v ( s i N o o v ) \hat{C}_v(si^{Noov}) C^v(siNoov)。u 的最高好奇心水平,用 P C L u PCLu PCLu 表示是 C ^ u ( s i N o o v ) \hat{C}_u(si^{Noov}) C^u(siNoov)上的点( ,)。 其中,0.24是siru的学习参数,0.48是sipu的学习参数。 类似地,v 的 P C L v PCLv PCLv是 C ^ v ( s i N o o v ) \hat{C}_v(si^{Noov}) C^v(siNoov)上的点( , ),而 sirv=0.36 和 sipv=0.49。 这些结果表明,由于激发了好奇心,u (v) 更愿意将大部分时间花在强度介于 0.24 和 0.48(0.36 和 0.49)之间的项目上。 我们的好奇心机制将通过 Wundt 曲线为新颖刺激强度在 [0.24, 0.48] ([0.36, 0.49]) 范围内的项目分配更高的好奇心分数。 值得注意的是,其他两个图(图 13b 和 13c)以几乎相同的方式提供了对好奇心的判断。 显然,我们使用 Wundt 曲线对好奇心进行建模具有可解释性的优势。
此外,用户在面对不同类型的刺激时会产生不同的反应。以 v 为例,与新颖刺激强度和复合刺激强度相比,v 可以容忍极高的冲突刺激强度(siconf=1,见图 13b)。这反映了即使 v 从她的社交同龄人那里收到了相同强度的正面响应和负面响应,v 也可能有一定的概率选择该项目。但是,参考文献5中提供的 Beta 分布无法描述类似的情况。因为两端(siconf= 0 和 siconf=1)实际上不是密度函数域的一部分。实际上,近三分之二的用户(6,040 人中的 2,064 人)未能通过使用 Beta 分布获得他们的 Wundt 曲线。因此,我们使用 Wundt 曲线建模的一个显着优势是它通常更准确地反映用户对刺激强度的反应,使其成为未来研究的合适且实用的方法。
7.4 实验3 SeCM 与现有推荐技术的比较
我们接下来的分析重点是将建议的 SeCM 与许多最先进的方法进行比较。结果连同相对改进的百分比(改进百分比)一起报告在表 2 中,其中选择 SeCM 的化合物作为基线。在 ML-1M 数据集上的推荐性能可以在表 2a 中找到,从中我们有以下发现:1)在所有好奇心驱动方法中,Compound 是最有效的。 SC 在所有多样性指标上都击败了 SeCM,但在精度损失方面表现不佳,高达 6.38% Precision@5 和 6.28% Precision@10。 Compound 在 Precision 上的表现与 UC 相当,也获得了显着的优势,例如在 ILS@5 上的提升 82.12%,在 AD@5 上的提升 55.36%。虽然,复合性能在 AD 和 Newness 上有时不如 CBRS。这些微小的差异(平均 0.03%)可能被 Compound 的 Precision@5 增长 1.48% 和 Precision@5 增长 1.36% 所掩盖。 2)当使用Precision作为评估指标时,PopRec表现最好,其次是IF-MF。然而,这种优势是以牺牲多样性为代价的。与 Compound 相关的是,PopRec 在 AD@5 中下降了 1.726%,在 AD@10 中下降了 1206%(啥?)。这可以归因于 PopRec 固有地为所有用户推送相同的推荐列表的事实。 3) Compound 以平均多样性的形式将 IF-MF 在 ILS 上提高了 48.45%,在 Newness 上提高了 14.41%,在 AD 上提高了 29.87%。这些结果可能意味着,在 Phase 3 完全从 CdRF 中移除的情况下,Compound 仍然可以实现有希望的多样性结果,同时仅损失 2.43% Precision@5 和 1.52% Precision@10。我们将这些归因于 Compound 的优势,它成功地描绘了个人的好奇心,导致在相关性和多样性之间达成妥协。
从表 2b、2c 和 2d 中,实验结果表明,Compound 在各种多样性措施方面始终优于所有其他竞争对手。同时,Compound 还保持着令人印象深刻的 Precision,仅次于 IF-MF 和 UC(以及在 Lthing 数据集上的 Precision@5 中的 PopRec)。然而,这种差异似乎可以忽略不计,因为小的精度损失带来了多样性的极大改善。例如,在 ABooks 数据集上,Compound 在 Precision@5 上与 UC 相比损失了 0.06%,但在多样性方面取得了显着改善(例如,ILS@5 上的 70.70%、AD@5 上的 58.67% 等)。与 IF-MF 和 PopRec 相比,在精度损失方面发现了类似的改进,显示了 Compound 的优越性。总而言之,我们提出的 SeCM(在复合情况下)在数据集上的表现要么与其他同类产品相当,要么优于其他同类产品。它在四个数据集上实现了非常强大的多样性表现,证明它确实推荐了更多样化的项目。在这些方面,它适合作为传统的面向精度的 RS 的有用补充。
7.5 实验4 CdRF 与现有好奇心技术的比较
以 IF-MF 为基准,第四系列实验旨在调查所提出的 CdRF 和现有的好奇心驱动方法(UC 和 CBRS)在获得多样性(ILS、AD、Newness 中的改进百分比)方面遭受的精度损失(精度降低百分比)。 表 3 分别报告了四个数据集的详细结果。 请注意,我们将 SC 从比较中排除,因为它直观地基于 R-MF 而不是 IF-MF,其中 R-MF 用于准确预测评级。
从四个数据集的结果中,我们有以下发现:1)在同等精度损失的情况下,与其他方法相比,CdRF 在提供多样性方面总是成功的。例如,在 ML-1M 数据集(表 3a)上,在 Precision@5 降低 1% 的情况下,CdRF 可以以 ILS@5 的形式比 IFMF 提高 29.75%。而CBRS只增加了6.58%的ILS@5,而UC甚至牺牲了129.91%的ILS@5。这清楚地表明 CdRF 可以有效地推荐更多样化的项目; 2) 只有 CdRF 在所有多样性度量上始终优于基线。这一观察结果与所提出的 SeCM 可以帮助增强 RS 多样性的直觉相吻合。但是CBRS和UC也采用了好奇心机制,结果不尽人意。一方面,虽然遵循 AOA 和 AOB 规则,但 CBRS 在数据集上的表现并不是很稳定,并且在某些情况下未能超越 IF-MF,尤其是在 Lthing 数据集上。主要原因可能是其Wundt曲线的建模方法,阻碍了准确捕捉个人好奇心。另一方面,UC 的表现最差。我们将损失部分归因于其计算方法,这可能不可避免地促进推荐列表中显示的热门项目,从而降低多样性性能。这些比较还证实,即使在好奇心基线表现不佳的情况下,CdRF 也是有效的; 3) CdRF 即使对精度的影响很小,也可以获得多样性增强。例如,在 ML-100K 数据集上,与 IF-MF 相比,CBRS 实现了多样性优势,直到失去了 3% 的精度。而 CdRF 迅速获得更多多样性,因为仅牺牲了 1% 的精度损失(表 3b)。事实上,我们也可以得出结论,如果允许 RS 容忍更多的精度损失,CdRF 可以实现更多的多样性。
综合而言,所提出的 CdRF 在四个数据集上的表现优于竞争对手,这支持可以通过同时捕获用户的相关性偏好和个人好奇心来提高整体推荐质量的观点。 更重要的是,这些结果也支持了这样一个结论,即 CdRF 可用于以可接受的精度快速生成多样化的项目,在推荐相关但多样化的项目方面表现出其稳定性、优越性和灵活性的优势。 此外,实验还表明CdRF非常通用,不仅在电影推荐上表现良好,在书籍推荐上也表现良好。 这些特性促进了 CdRF 更容易在现实中应用。
8、相关工作
8.1 改善多样性的建议
参考文献 [30] 提出了个人流行趋势匹配 (PPTM) 以根据发现的个人流行趋势 (PPT) 推荐新项目。 参考文献 [31] 通过利用历史餐饮模式、社会人口特征和餐厅属性,提出了一种基于新奇寻求的餐饮推荐系统(NDRS)。参考文献[32] 引入了一个基于聚类的框架(KRCF)来增加新颖性和多样性。 参考文献 [1] 和 [33]针对单阶段方法的问题提出了建议。 其中,文献[1] 在 MF 中加入了额外的多样性增强约束。文献 [33] 通过基于矩阵完成框架的单个(联合)优化模型利用评级和项目元数据来实现准确性-多样性平衡。
8.2 好奇心驱动推荐
尽管好奇心已在心理学中得到广泛研究,并逐渐应用于神经科学和社会学领域 [34]、[35]、[36],但据我们所知,在 RS 的情境下该主题仅有以下四项工作。 Santos [2] 提出了一种混合 RS,将每个人的好奇心作为推荐南美洲景点的决定性因素。 第一个要求是从志愿者那里收集 CEI-II 问卷。 然后,它为好奇心较低的用户执行基于内容的推荐,并为好奇心较高的用户执行基于协作的推荐。 然而,除了RS服务的正常使用之外,还需要额外的人工干预。参考文献[3] 模拟了意外引发的好奇心。同一作者还在参考文献[4]中提出了另一种方法用于好奇心驱动的推荐。他们首先对基于香农熵和 Damster-Shafter 理论的用户不确定性好奇心进行建模,然后通过整合用户偏好和不确定性对项目进行排名。然而,吴的作品推荐了刺激性最强的项目,而忽略了好奇心的个体差异。参考文献 [5] 提出了一种基于好奇心的推荐系统(CBRS),该系统生成具有个性化新颖性的推荐,以适应用户的好奇心水平。它提出了一个用户好奇心的计算模型,称为概率好奇心模型(PCM),以使用 Beta 分布函数对用户的好奇心进行建模。然而,CBRS 有几个局限性:1)不能利用社会因素,因为好奇心除了与个人背景有关也与社会背景有关[6] 2) 缺乏可解释性和泛化性,因为如果不满足 beta 分布的特征,它总是无法工作; 3)在很多场景中,信息仅限于物品的评分或访问信息,音乐类型等物品特征可能不可用或不完整[37]。
9、结论和展望
传统的 RS 存在精度过拟合问题,这会抑制用户对推送项目的热情。在心理学中,好奇心是推动探索行为的核心和动力。受此启发,我们提出了一个好奇心驱动的推荐框架(CdRF)。它通过 Borda 计数灵活地将一种新颖的刺激引发的好奇心机制 (SeCM) 与现有的面向准确性的 MF 方法联系起来,以推荐相关但又多样化的项目,从而促进用户对 RS 的参与。 SeCM 本质上是 CdRF 的重要组成部分,旨在捕捉个人的好奇心。 SeCM 背后的理由是,当出现在项目上的刺激强度对于目标用户而言只是略微超最佳时,探索更有可能发生。具体而言,SeCM 限定了新颖性和冲突刺激强度的复合,并使用 Wundt 曲线以及 AOA 和 AOB 规则对个性化好奇心进行建模。两个电影和两个书籍数据集的实验表明:1)SeCM 确保推荐匹配个人好奇心水平,同时有助于多样化推荐; 2) CdRF 不仅优于最先进的基于好奇心的方法,而且还最大化了推荐的多样性,以获得(给定的)可接受的准确性损失。
尽管好奇心驱动探索的问题很大,但我们相信这项工作是向前迈出的一步,并提供了一些关键思想来加强 RS 性能。在未来的工作中可以进行几种可能的扩展。第一个是打破对所有用户的等价分配,因为每个人实际上对不同的刺激具有不同的敏感性。例如,与新奇刺激相比,人们可能更容易受到冲突刺激的干扰。另一个有趣的扩展是将源于好奇心的危险(如“好奇害死猫”[36] 所表达的那样)考虑在内,这也可能会影响用户的在线行为。此外,其他引起好奇心的因素,如复杂性、不一致等,将被调查和纳入以提升整体推荐结果。此外,迫切需要设计组合度量以同时测量准确性和多样性。