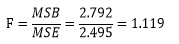0.双因素方差分析的分类
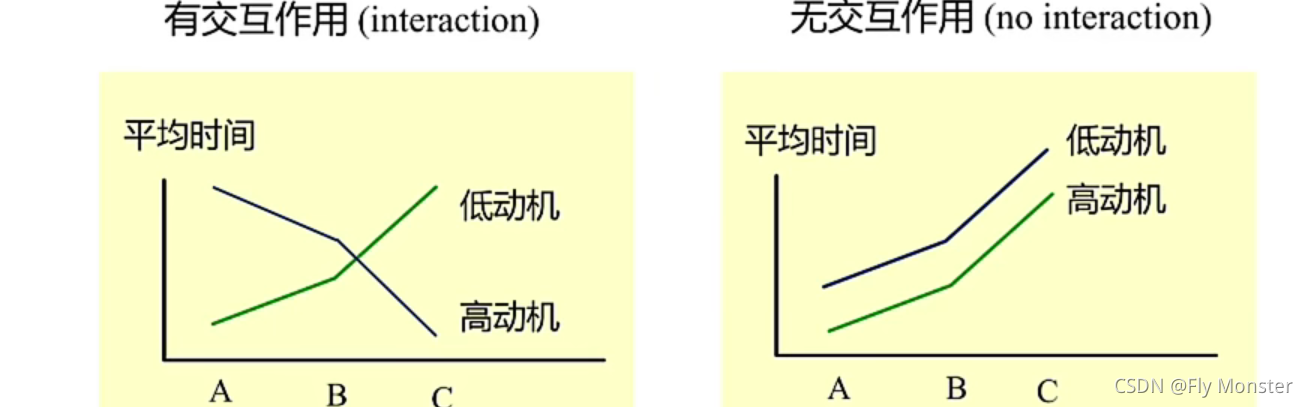
- 无交互作用的方差分析
假定因素 A A A和因素 B B B的效应之间是相互独立的,不存在相互关系。 - 有交互作用的方差分析
假定因素 A A A和因素 B B B的结合会产生出一种新的效应。
无交互作用的双因素方差分析
1.形式
假定要考察两个因素 A , B A,B A,B对某项指标的影响,因素 A A A取 s s s个水平 A 1 , A 2 , … , A s A_{1}, A_{2}, \dots, A_{s} A1,A2,…,As,因素 B B B取 r r r个水平 B 1 , B 2 , … , B r B_{1}, B_{2}, \dots, B_{r} B1,B2,…,Br,在 A , B A,B A,B的每队组合水平 ( A i , B j ) \left(A_{i}, B_{j}\right) (Ai,Bj)上作一次试验,试验结果为 X i j , i = 1 , … , s ; j = 1 , … , r X_{i j}, i=1, \dots, s ;\space j=1, \dots, r Xij,i=1,…,s; j=1,…,r。所有 X i j X_{ij} Xij独立,数据列于下表:
| 因素 | B 1 B_1 B1 | B 2 B_2 B2 | … | B s B_s Bs |
|---|---|---|---|---|
| A 1 A_1 A1 | X 11 X_{11} X11 | X 12 X_{12} X12 | … | X 1 s X_{1s} X1s |
| A 2 A_2 A2 | X 21 X_{21} X21 | X 22 X_{22} X22 | … | X 2 s X_{2s} X2s |
| … | … | … | … | … |
| A r A_r Ar | X r 1 X_{r1} Xr1 | X r 2 X_{r2} Xr2 | … | X r s X_{rs} Xrs |
2.前期工作
- 作出假设
设搭配 ( A i , B j ) \left(A_{i}, B_{j}\right) (Ai,Bj)下的试验结果为 X i j X_{ij} Xij,假定 X i j ∼ N ( a i j , σ 2 ) X_{i j} \sim N\left(a_{i j}, \sigma^{2}\right) Xij∼N(aij,σ2),则问题归结为检验假设:
H 0 A : a 1 j = a 2 j = ⋯ = a j j , j = 1 , 2 , ⋯ , s H 0 B : a i 1 = a i 2 = ⋯ = a i r , i = 1 , 2 , ⋯ , r \begin{aligned} &H_{0 A}: a_{1 j}=a_{2 j}=\cdots=a_{j j}, j=1,2, \cdots, s\\ &H_{0 B}: a_{i 1}=a_{i 2}=\cdots=a_{i r}, i=1,2, \cdots, r \end{aligned} H0A:a1j=a2j=⋯=ajj,j=1,2,⋯,sH0B:ai1=ai2=⋯=air,i=1,2,⋯,r - 平方和分解
与单因素方差分析类似地:
S A S_A SA是由因素 A A A的不同效应和随机误差引起的偏差
S B S_B SB是由因素 B B B的不同效应和随机误差引起的偏差
S e S_e Se是由随机误差引起的偏差
记:
n = r s , X ˉ i = 1 s ∑ j = 1 s X i j , X ˉ ⋅ j = 1 r ∑ i = 1 r X i j T i ⋅ = ∑ j = 1 s X i j , T ⋅ j = ∑ i = 1 r X i j X ˉ = 1 r s ∑ i = 1 r ∑ j = 1 s X i j , T = ∑ i = 1 r ∑ j = 1 s X i j i = 1 , 2 , ⋯ , r ; j = 1 , 2 , ⋯ , s n=r s, \bar{X}_{i}=\frac{1}{s} \sum_{j=1}^{s} X_{i j}, \bar{X}_{\cdot j}=\frac{1}{r} \sum_{i=1}^{r} X_{i j}\\ T_{i \cdot}=\sum_{j=1}^{s} X_{i j}, T_{\cdot j}=\sum_{i=1}^{r} X_{i j}\\ \bar{X}=\frac{1}{r s} \sum_{i=1}^{r} \sum_{j=1}^{s} X_{i j}, T=\sum_{i=1}^{r} \sum_{j=1}^{s} X_{i j}\\ i=1,2, \cdots, r ; j=1,2, \cdots, s n=rs,Xˉi=s1j=1∑sXij,Xˉ⋅j=r1i=1∑rXijTi⋅=j=1∑sXij,T⋅j=i=1∑rXijXˉ=rs1i=1∑rj=1∑sXij,T=i=1∑rj=1∑sXiji=1,2,⋯,r;j=1,2,⋯,s
于是:
S T = ∑ i = 1 r ∑ j = 1 s X i j 2 − T 2 r s , S A = 1 s ∑ i = 1 r T i ⋅ 2 − T 2 r s S B = 1 r ∑ j = 1 s T ⋅ j 2 − T 2 r s , S e = S T − S A − S B S_{T}=\sum_{i=1}^{r} \sum_{j=1}^{s} X_{i j}^{2}-\frac{T^{2}}{r s}, S_{A}=\frac{1}{s} \sum_{i=1}^{r} T_{i \cdot}^{2}-\frac{T^{2}}{r s}\\ S_{B}=\frac{1}{r} \sum_{j=1}^{s} T_{\cdot j}^{2}-\frac{T^{2}}{r s},S_{e}=S_{T}-S_{A}-S_{B} ST=i=1∑rj=1∑sXij2−rsT2,SA=s1i=1∑rTi⋅2−rsT2SB=r1j=1∑sT⋅j2−rsT2,Se=ST−SA−SB
3.检验假设
比较 S A S_A SA与 S E S_E SE的值来检验假设 H 0 A H_{0A} H0A
比较 S B S_B SB与 S E S_E SE的值来检验假设 H 0 B H_{0B} H0B
- 定理
S T , S A , S B S_T,S_A,S_B ST,SA,SB相互独立,且 1 σ 2 S e ∼ χ 2 ( ( s − 1 ) ( r − 1 ) ) \frac{1}{\sigma^{2}} S_{e} \sim \chi^{2}((s-1)(r-1)) σ21Se∼χ2((s−1)(r−1))
当 H 0 A H_{0A} H0A成立时,有:
F A = S A / σ 2 r − 1 / S e / σ 2 ( r − 1 ) ( s − 1 ) = ( s − 1 ) S A S e ∼ F ( r − 1 , ( r − 1 ) ( s − 1 ) ) F_{A}=\frac{S_{A} / \sigma^{2}}{r-1} / \frac{S_{e} / \sigma^{2}}{(r-1)(s-1)}=\frac{(s-1) S_{A}}{S_{e}} \sim F(r-1,(r-1)(s-1)) FA=r−1SA/σ2/(r−1)(s−1)Se/σ2=Se(s−1)SA∼F(r−1,(r−1)(s−1))
当 H 0 B H_{0B} H0B成立时,有:
F B = S B / σ 2 s − 1 / S e / σ 2 ( r − 1 ) ( s − 1 ) = ( r − 1 ) S A S e ∼ F ( s − 1 , ( r − 1 ) ( s − 1 ) ) F_{B}=\frac{S_{B} / \sigma^{2}}{s-1} / \frac{S_{e} / \sigma^{2}}{(r-1)(s-1)}=\frac{(r-1) S_{A}}{S_{e}} \sim F(s-1,(r-1)(s-1)) FB=s−1SB/σ2/(r−1)(s−1)Se/σ2=Se(r−1)SA∼F(s−1,(r−1)(s−1)) - 拒绝域
H 0 A H_{0A} H0A的拒绝域为:
F A ≥ F α ( s − 1 , ( s − 1 ) ( r − 1 ) ) F_{A} \geq F_{\alpha}(s-1,(s-1)(r-1)) FA≥Fα(s−1,(s−1)(r−1))
H 0 B H_{0B} H0B的拒绝域为:
F B ≥ F α ( r − 1 , ( s − 1 ) ( r − 1 ) ) F_{B} \geq F_{\alpha}(r-1,(s-1)(r-1)) FB≥Fα(r−1,(s−1)(r−1)) - 方差分析表
|方差来源 |平方和 |自由度 | F F F值 |临界值 |
| :------------: | :------------: | :------------: | :------------: | :------------: |
|因素 A A A | S A S_A SA | r − 1 r-1 r−1 | F A = ( s − 1 ) S A S e F_{A}=\frac{(s-1) S_{A}}{S_{e}} FA=Se(s−1)SA | F A α F_{A\alpha} FAα |
|因素 B B B | S B S_B SB | s − 1 s-1 s−1 | F B = ( r − 1 ) S B S e F_{B}=\frac{(r-1) S_{B}}{S_{e}} FB=Se(r−1)SB | F B α F_{B\alpha} FBα |
|试验误差 | S e S_e Se | ( r − 1 ) ( s − 1 ) (r-1)(s-1) (r−1)(s−1) | | |
|总和 | S T S_T ST | n − 1 n-1 n−1 | | |
4.实现
- 例题
为了研究不同地点,不同季节大气飘尘含量的差异性,对地点 A A A取三个不同水平,对季节 B B B取四个不同水平,在不同组合(A_i,B_j)下各测一次大气飘尘含量,结果建下表,请问研究地点间的差异和季节间的差异对大气飘尘含量有无影响? ( α = 0.05 ) (\alpha=0.05) (α=0.05)
| 因素 | B 1 B_1 B1 | B 2 B_2 B2 | B 3 B_3 B3 | B 4 B_4 B4 |
|---|---|---|---|---|
| A 1 A_1 A1 | 1.150 | 0.614 | 0.475 | 0.667 |
| A 2 A_2 A2 | 1.200 | 0.620 | 0.420 | 0.880 |
| A 3 A_3 A3 | 0.940 | 0.379 | 0.200 | 0.540 |
-
Excel求解
录入数据:
在方差分析选项中选择“无重复双因素方差分析”,选中分析区域, α \alpha α设为0.05,单击“确定”:
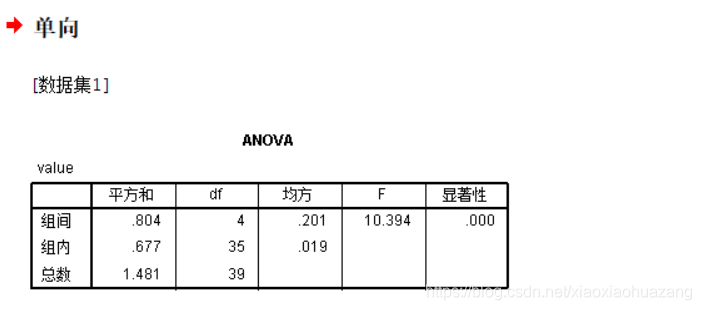
可在新工作表中看到结果:
-
MATLAB求解
function annova_solve()x = [1.150, 0.614, 0.475, 0.667;1.200, 0.620, 0.420, 0.880;0.940, 0.379, 0.200, 0.540];p = anova2(x);
end
运行结果:
- Python求解
import pandas as pd
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lmdf = pd.read_csv('D:\Data\ex_2way_annova.csv')
print(df)
model = ols('content ~ season + location', data = df).fit()
table = anova_lm(model)
print(table)
运行结果:
- 结论
F A = 23.848 > F A α = 10.92 , F B = 88.848 > F B α = 9.78 F_{A}=23.848>F_{A \alpha}=10.92, F_{B}=88.848>F_{B \alpha}=9.78 FA=23.848>FAα=10.92,FB=88.848>FBα=9.78,拒绝 H 0 A , H 0 B H_{0A},H_{0B} H0A,H0B,认为两个因素都有影响。
有交互作用的双因素方差分析
1.形式
假定要考察两个因素 A , B A,B A,B对某项指标的影响,因素 A A A取 s s s个水平 A 1 , A 2 , … , A s A_{1}, A_{2}, \dots, A_{s} A1,A2,…,As,因素 B B B取 r r r个水平 B 1 , B 2 , … , B r B_{1}, B_{2}, \dots, B_{r} B1,B2,…,Br,在 A , B A,B A,B的每队组合水平 ( A i , B j ) \left(A_{i}, B_{j}\right) (Ai,Bj)上尸检结果独立地服从 N ( μ i j , σ 2 ) N\left(\mu_{i j}, \sigma^{2}\right) N(μij,σ2)分布,如下表:
| 因素 | B 1 B_1 B1 | B 2 B_2 B2 | … | B s B_s Bs |
|---|---|---|---|---|
| A 1 A_1 A1 | X 111 , . . . , X 11 t X_{111},...,X_{11t} X111,...,X11t | X 121 , . . . , X 12 t X_{121},...,X_{12t} X121,...,X12t | … | X 1 s 1 , . . . , X 1 s t X_{1s1},...,X_{1st} X1s1,...,X1st |
| A 2 A_2 A2 | X 211 , . . . , X 21 t X_{211},...,X_{21t} X211,...,X21t | X 221 , . . . , X 22 t X_{221},...,X_{22t} X221,...,X22t | … | X 2 s 1 , . . . , X 2 s t X_{2s1},...,X_{2st} X2s1,...,X2st |
| … | … | … | … | … |
| A r A_r Ar | X r 11 , . . . , X r 1 t X_{r11},...,X_{r1t} Xr11,...,Xr1t | X r 21 , . . . , X r 2 t X_{r21},...,X_{r2t} Xr21,...,Xr2t | … | X r s 1 , . . . , X r s t X_{rs1},...,X_{rst} Xrs1,...,Xrst |
2.参数
为了方便研究,令:
μ = 1 r s ∑ i = 1 r ∑ j = 1 s μ i j μ i . = 1 s ∑ j = 1 s μ i j α i = μ i . − μ i = 1 , 2 , … , r μ . j = 1 r ∑ i = 1 r μ i j β j = μ . j − μ j = 1 , 2 , … , s \begin{aligned} &\mu=\frac{1}{r s} \sum_{i=1}^{r} \sum_{j=1}^{s} \mu_{i j}\\ &\mu_{i .}=\frac{1}{s} \sum_{j=1}^{s} \mu_{i j} \quad \alpha_{i}=\mu_{i .}-\mu \quad i=1,2, \ldots, r\\ &\mu_{. j}=\frac{1}{r} \sum_{i=1}^{r} \mu_{i j} \quad \beta_{j}=\mu_{. j}-\mu \quad j=1,2, \ldots, s \end{aligned} μ=rs1i=1∑rj=1∑sμijμi.=s1j=1∑sμijαi=μi.−μi=1,2,…,rμ.j=r1i=1∑rμijβj=μ.j−μj=1,2,…,s
称 μ \mu μ为一般平均值, α i \alpha_{i} αi为因素 A A A的第 i i i个水平的效应,有如下关系式:
∑ i = 1 r α i = 0 ∑ j = 1 s β j = 0 \sum_{i=1}^{r} \alpha_{i}=0 \quad \sum_{j=1}^{s} \beta_{j}=0 i=1∑rαi=0j=1∑sβj=0
若 μ i j ≠ μ + α i + β j \mu_{i j} \neq \mu+\alpha_{i}+\beta_{j} μij=μ+αi+βj,则称 γ i j = μ i j − μ − α i − β j \gamma_{i j}=\mu_{i j}-\mu-\alpha_{i}-\beta_{j} γij=μij−μ−αi−βj为因素 A A A的第 i i i个水平与因素 B B B的第 j j j个水平的交互效应,它们满足关系式:
∑ i = 1 r γ i j = 0 , j = 1 , 2 , … , s ∑ j = 1 s γ i j = 0 , i = 1 , 2 , … , r \begin{aligned} &\sum_{i=1}^{r} \gamma_{i j}=0, \quad j=1,2, \ldots, s\\ &\sum_{j=1}^{s} \gamma_{i j}=0, \quad i=1,2, \ldots, r \end{aligned} i=1∑rγij=0,j=1,2,…,sj=1∑sγij=0,i=1,2,…,r
3.模型与假设
- 有交互的双因素方差分析模型
X i j k = μ + α i + β j + γ i j + ε i j k ∑ i = 1 r α i = 0 , ∑ j = 1 s β j = 0 ∑ i = 1 r γ i j = 0 , ∑ j = 1 s γ i j = 0 ε i j k ∼ N ( 0 , σ 2 ) , 且 相 互 独 立 i = 1 , 2 , … , r ; j = 1 , 2 , … , s ; k = 1 , 2 , … , t \begin{aligned} &X_{i j k}=\mu+\alpha_{i}+\beta_{j}+\gamma_{i j}+\varepsilon_{i j k}\\ &\sum_{i=1}^{r} \alpha_{i}=0, \quad \sum_{j=1}^{s} \beta_{j}=0\\ &\sum_{i=1}^{r} \gamma_{i j}=0, \quad \sum_{j=1}^{s} \gamma_{i j}=0\\ &\varepsilon_{i j k} \sim N\left(0, \sigma^{2}\right),且相互独立 \end{aligned}\\ i=1,2, \ldots, r ; \quad j=1,2, \ldots, s ; \quad k=1,2, \ldots, t Xijk=μ+αi+βj+γij+εijki=1∑rαi=0,j=1∑sβj=0i=1∑rγij=0,j=1∑sγij=0εijk∼N(0,σ2),且相互独立i=1,2,…,r;j=1,2,…,s;k=1,2,…,t - 需要检验的假设
H 01 : α 1 = α 2 = … = α r = 0 H 02 : β 1 = β 2 = … = β s = 0 H 03 : γ y ˉ = 0 , ∀ i , j \begin{aligned} &H_{01}: \alpha_{1}=\alpha_{2}=\ldots=\alpha_{r}=0\\ &H_{02}: \beta_{1}=\beta_{2}=\ldots=\beta_{s}=0\\ &H_{03}: \gamma_{\bar{y}}=0, \quad \forall i, j \end{aligned} H01:α1=α2=…=αr=0H02:β1=β2=…=βs=0H03:γyˉ=0,∀i,j
4.平方和分解
- 记号引入
X = 1 r s t ∑ i = 1 r ∑ j = 1 s ∑ k = 1 t X i j k X i j ⋅ = ∑ k = 1 t X i j k , X ˉ i j ⋅ = 1 t X i j ⋅ , i = 1 , 2 , … , r ; j = 1 , 2 , … , s X i ⋅ ⋅ = ∑ j = 1 s ∑ k = 1 t X i j k , X ˉ i ⋅ ⋅ = 1 s t X i ⋅ ⋅ , i = 1 , 2 , … , r X ⋅ j ⋅ = ∑ j = 1 r ∑ k = 1 t X i j k , X ˉ ⋅ j ⋅ = 1 r t X i ⋅ ⋅ , j = 1 , 2 , … , s X=\frac{1}{rst} \sum_{i=1}^{r} \sum_{j=1}^{s} \sum_{k=1}^{t} X_{i j k}\\ \begin{aligned} &X_{ij\cdot} =\sum_{k=1}^{t} X_{i j k}, \quad \bar{X}_{i j\cdot} =\frac{1}{t} X_{i j\cdot} , \quad i=1,2, \ldots, r ; \quad j=1,2, \ldots, s\\ &X_{i\cdot\cdot} =\sum_{j=1}^{s} \sum_{k=1}^{t} X_{i j k}, \quad \bar{X}_{i \cdot \cdot}=\frac{1}{s t} X_{i\cdot\cdot}, \quad i=1,2, \ldots, r\\ &X_{\cdot j\cdot}=\sum_{j=1}^{r} \sum_{k=1}^{t} X_{i j k}, \quad \bar{X}_{\cdot j\cdot}=\frac{1}{r t} X_{i\cdot\cdot}, \quad j=1,2, \ldots, s \end{aligned} X=rst1i=1∑rj=1∑sk=1∑tXijkXij⋅=k=1∑tXijk,Xˉij⋅=t1Xij⋅,i=1,2,…,r;j=1,2,…,sXi⋅⋅=j=1∑sk=1∑tXijk,Xˉi⋅⋅=st1Xi⋅⋅,i=1,2,…,rX⋅j⋅=j=1∑rk=1∑tXijk,Xˉ⋅j⋅=rt1Xi⋅⋅,j=1,2,…,s
由此可得:
X ˉ = μ + s ˉ X ˉ i j ⋅ = μ + α i + β j + γ i j + ε ˉ i j ⋅ X ˉ i ⋅ ⋅ = μ + α j + ε ˉ i ⋅ ⋅ X ˉ ⋅ j ⋅ = μ + β j + ε ˉ ⋅ j ⋅ \begin{aligned} &\bar{X}=\mu+\bar{s}\\ &\bar{X}_{i j\cdot}=\mu+\alpha_{i}+\beta_{j}+\gamma_{i j}+\bar{\varepsilon}_{i j\cdot}\\ &\bar{X}_{i\cdot\cdot}=\mu+\alpha_{j}+\bar{\varepsilon}_{i\cdot\cdot}\\ &\bar{X}_{\cdot j \cdot}=\mu+\beta_{j}+\bar{\varepsilon}_{\cdot j\cdot} \end{aligned} Xˉ=μ+sˉXˉij⋅=μ+αi+βj+γij+εˉij⋅Xˉi⋅⋅=μ+αj+εˉi⋅⋅Xˉ⋅j⋅=μ+βj+εˉ⋅j⋅ - 平方和分解
S T = ∑ i = 1 r ∑ j = 1 s ∑ k = 1 t ( X i j k − X ˉ ) 2 = S E + S A + S B + S A × B \begin{aligned} &S_{T}=\sum_{i=1}^{r} \sum_{j=1}^{s} \sum_{k=1}^{t}\left(X_{i j k}-\bar{X}\right)^{2}\\ &=S_{E}+S_{A}+S_{B}+S_{A \times B} \end{aligned} ST=i=1∑rj=1∑sk=1∑t(Xijk−Xˉ)2=SE+SA+SB+SA×B - 误差平方和
试验的随机波动引起的误差。
S E = ∑ i = 1 r ∑ j = 1 s ∑ k = 1 t ( X i j k − X ˉ i j ⋅ ) 2 S_{E}=\sum_{i=1}^{r} \sum_{j=1}^{s} \sum_{k=1}^{t}\left(X_{i j k}-\bar{X}_{i j\cdot} \right)^{2} SE=i=1∑rj=1∑sk=1∑t(Xijk−Xˉij⋅)2 - 因子 A A A的偏差平方和
除了反映了试验的随机波动引起的误差外,还反映了因子A的效应间的差异。
S A = ∑ i = 1 r s t ( X ˉ i ⋅ ⋅ − X ˉ ) 2 S_{A}=\sum_{i=1}^{r} s t\left(\bar{X}_{i\cdot\cdot}-\bar{X}\right)^{2} SA=i=1∑rst(Xˉi⋅⋅−Xˉ)2 - 因子 B B B的偏差平方和
除了反映了试验的随机波动引起的误差外,还反映了因子B的效应间的差异。
S B = ∑ j = 1 s r t ( X ˉ ⋅ j ⋅ − X ˉ ) 2 S_{B}=\sum_{j=1}^{s} r t\left(\bar{X}_{\cdot j\cdot}-\bar{X}\right)^{2} SB=j=1∑srt(Xˉ⋅j⋅−Xˉ)2 - 交互作用的偏差平方和
除了反映了试验的随机波动引起的误差外,还反映了交互效应的差异所引起的波动。
S A × B = ∑ i = 1 r ∑ j = 1 s t ( X ˉ i j ⋅ − X ˉ i ⋅ ⋅ − X ˉ ⋅ j ⋅ + X ˉ ) 2 S_{A \times B}=\sum_{i=1}^{r} \sum_{j=1}^{s} t\left(\bar{X}_{i j\cdot}-\bar{X}_{i \cdot \cdot}-\bar{X}_{\cdot j \cdot}+\bar{X}\right)^{2} SA×B=i=1∑rj=1∑st(Xˉij⋅−Xˉi⋅⋅−Xˉ⋅j⋅+Xˉ)2 - 计算公式
S T = ∑ i = 1 r ∑ j = 1 s ∑ k = 1 t X i j k 2 − n X ˉ 2 f T = r s t − 1 S A = 1 s t ∑ i = 1 r X i . . 2 − n X ˉ 2 f A = r − 1 S B = 1 r t ∑ i = 1 r X . j . 2 − n X ˉ 2 f B = s − 1 S A × B = 1 t ∑ i = 1 r ∑ j = 1 s X i j . 2 − n X ˉ 2 − S A − S B f A × B = ( r − 1 ) ( s − 1 ) S E = S T − S A − S B − S A X B f E = r s ( t − 1 ) \begin{aligned} &S_{T}=\sum_{i=1}^{r} \sum_{j=1}^{s} \sum_{k=1}^{t} X_{i j k}^{2}-n \bar{X}^{2} \quad f_{T}=r s t-1\\ &S_{A}=\frac{1}{s t} \sum_{i=1}^{r} X_{i . .}^{2}-n \bar{X}^{2} \quad \quad f_{A}=r-1\\ &S_{B}=\frac{1}{r t} \sum_{i=1}^{r} X_{. j .}^{2}-n \bar{X}^{2} \quad f_{B}=s-1\\ &S_{A \times B}=\frac{1}{t} \sum_{i=1}^{r} \sum_{j=1}^{s} X_{i j .}^{2}-n \bar{X}^{2}-S_{A}-S_{B} \quad f_{A \times B}=(r-1)(s-1)\\ &S_{E}=S_{T}-S_{A}-S_{B}-S_{A X B} \quad f_{E}=r s(t-1) \end{aligned} ST=i=1∑rj=1∑sk=1∑tXijk2−nXˉ2fT=rst−1SA=st1i=1∑rXi..2−nXˉ2fA=r−1SB=rt1i=1∑rX.j.2−nXˉ2fB=s−1SA×B=t1i=1∑rj=1∑sXij.2−nXˉ2−SA−SBfA×B=(r−1)(s−1)SE=ST−SA−SB−SAXBfE=rs(t−1)
5.假设检验
- 检验统计量
当 H 01 H_{01} H01为真时:
F A = S A / ( r − 1 ) S E / r s ( t − 1 ) ∼ F ( r − 1 , r s ( t − 1 ) ) F_{A}=\frac{S_{A} /(r-1)}{S_{E} / r s(t-1)} \sim F(r-1, r s(t-1)) FA=SE/rs(t−1)SA/(r−1)∼F(r−1,rs(t−1))
当 H 02 H_{02} H02为真时:
F B = S B / ( s − 1 ) S E / r s ( t − 1 ) ∼ F ( s − 1 , r s ( t − 1 ) ) F_{B}=\frac{S_{B} /(s-1)}{S_{E} / r s(t-1)} \sim F(s-1, r s(t-1)) FB=SE/rs(t−1)SB/(s−1)∼F(s−1,rs(t−1))
当 H 03 H_{03} H03为真时:
F A × B = S A × B / ( r − 1 ) ( s − 1 ) S E / r s ( t − 1 ) ∼ F ( ( r − 1 ) ( s − 1 ) , r s ( t − 1 ) ) F_{A \times B}=\frac{S_{A \times B} /(r-1)(s-1)}{S_{E} / r s(t-1)} \sim F((r-1)(s-1), r s(t-1)) FA×B=SE/rs(t−1)SA×B/(r−1)(s−1)∼F((r−1)(s−1),rs(t−1)) - 假设的拒绝
对给定的显著性水平 α \alpha α:
当 F A > F 1 − α ( r − 1 , r s ( t − 1 ) ) F_A>F_{1-\alpha}(r-1,rs(t-1)) FA>F1−α(r−1,rs(t−1))时拒绝 H 01 H_{01} H01
当 F B > F 1 − α ( s − 1 , r s ( t − 1 ) ) F_B>F_{1-\alpha}(s-1,rs(t-1)) FB>F1−α(s−1,rs(t−1))时拒绝 H 02 H_{02} H02
当 F A × B > F 1 − α ( ( r − 1 ) ( s − 1 ) , r s ( t − 1 ) ) F_{A\times B}>F_{1-\alpha}((r-1)(s-1),rs(t-1)) FA×B>F1−α((r−1)(s−1),rs(t−1))时拒绝 H 03 H_{03} H03 - 方差分析表
| 来源 | 平方和 | 自由度 | 均方和 | F F F值 | 显著性 |
|---|---|---|---|---|---|
| 因子 A A A | S A S_A SA | r − 1 r-1 r−1 | S A / ( r − 1 ) S_A/(r-1) SA/(r−1) | F A F_A FA | |
| 因子 B B B | S B S_B SB | s − 1 s-1 s−1 | S B / ( s − 1 ) S_B/(s-1) SB/(s−1) | F B F_B FB | |
| A × B A\times B A×B | S A × B S_{A\times B} SA×B | ( r − 1 ) ( s − 1 ) (r-1)(s-1) (r−1)(s−1) | S A × B ( r − 1 ) ( s − 1 ) \frac{S_{A\times B}}{(r-1)(s-1)} (r−1)(s−1)SA×B | F A × B F_{A \times B} FA×B | |
| 误差 | S E S_E SE | r s ( t − 1 ) rs(t-1) rs(t−1) | S E / r s ( t − 1 ) S_E/rs(t-1) SE/rs(t−1) | ||
| 总和 | S T S_T ST | r s t − 1 rst-1 rst−1 |
一般,当 F > F 0.99 F>F_{0.99} F>F0.99时,称因子的影响高度显著,记为“**”;当 F 0.99 > F ≥ F 0.95 F_{0.99}>F≥F_{0.95} F0.99>F≥F0.95时,称因子的影响显著,记为“*”;当 F < F 0.95 F<F_{0.95} F<F0.95时, 称因子无显著影响,即认为因子各水平间无差异。
6.实现
- 例题
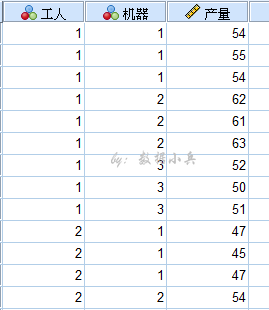
在某化工生产中为了提高收率,选了三种不同浓度 A A A,四种不同温度 B B B做试验。在同一浓度与同一温度组合下各做二次试验,其收率数据如下而计算表所列(数据均已减去75)。试检验不同浓度,不同温度以及它们间的交互作用对收率有无显著影响。
| 因素 | B 1 B_1 B1 | B 2 B_2 B2 | B 3 B_3 B3 | B 4 B_4 B4 | X i ⋅ ⋅ X_{i\cdot \cdot} Xi⋅⋅ | X i ⋅ ⋅ 2 X^2_{i\cdot \cdot} Xi⋅⋅2 |
|---|---|---|---|---|---|---|
| A 1 A_1 A1 | 14,10 | 11,11 | 13,9 | 10,12 | 90 | 8100 |
| A 2 A_2 A2 | 9,7 | 10,8 | 7,11 | 6,10 | 68 | 4624 |
| A 3 A_3 A3 | 5,11 | 13,14 | 12,13 | 14,10 | 92 | 8464 |
| X ⋅ j ⋅ X_{\cdot j\cdot} X⋅j⋅ | 56 | 67 | 65 | 62 | 250 | 21188 |
| X ⋅ j ⋅ 2 X^2_{\cdot j\cdot} X⋅j⋅2 | 3136 | 4489 | 4225 | 3844 | 15694 |
- C++求解
#include<bits/stdc++.h>
using namespace std;int main()
{int r = 3, s = 4, t = 2;double x[10][10][10]= {{{14,10},{11,11},{13, 9},{10,12}}, //data{{ 9, 7},{10, 8},{ 7,11},{ 6,10}},{{ 5,11},{13,14},{12,13},{14,10}}};double n_sq_x_bar = 0;double sq_x = 0;double x_ijdot = 0;double tmp = 0, tmp1 = 0, tmp2 = 0;double x_dot_j_dot[10];memset(x_dot_j_dot, 0, sizeof(x_dot_j_dot));double x_i_dot_dot[10];memset(x_i_dot_dot, 0, sizeof(x_i_dot_dot));for(int i = 0; i < r; ++i){for(int j = 0; j < s; ++j){for(int k = 0; k < t; ++k){x_dot_j_dot[j] += x[i][j][k];x_i_dot_dot[i] += x[i][j][k];tmp += x[i][j][k];n_sq_x_bar += x[i][j][k];sq_x += x[i][j][k] * x[i][j][k];}x_ijdot += tmp * tmp;tmp = 0;}}double sum_x_dot_j_dot = 0;for(int i = 0; i < s; ++i){sum_x_dot_j_dot += x_dot_j_dot[i] * x_dot_j_dot[i];}double sum_x_i_dot_dot = 0;for(int i = 0; i < r; ++i){sum_x_i_dot_dot += x_i_dot_dot[i] * x_i_dot_dot[i];}// cout << sum_x_dot_j_dot << " " << sum_x_i_dot_dot << endl;n_sq_x_bar /= 24;n_sq_x_bar *= n_sq_x_bar;n_sq_x_bar *= 24;// cout << n_sq_x_bar << " " << sq_x << " " << x_ijdot << endl;double S_T = sq_x - n_sq_x_bar;double S_A = sum_x_i_dot_dot / (s * t) - n_sq_x_bar;double S_B = sum_x_dot_j_dot / (r * t) - n_sq_x_bar;double S_AB = (1.0 / t) * x_ijdot - n_sq_x_bar - S_A - S_B;double S_E = S_T - S_A - S_B - S_AB;// cout << S_T << " " << S_A << " " << S_B << " " << S_AB << endl;double F_A = (S_A / (r - 1)) / (S_E / (r * s * (t - 1)));double F_B = (S_B / (s - 1)) / (S_E / (r * s * (t - 1)));double F_AB = (S_AB / ((r - 1) * (s - 1))) / (S_E / (r * s * (t - 1)));// cout << "F_A = " << F_A << "\nF_B = " << F_B << "\nF_AB = " << F_AB << endl;cout << "source\tdf\tSS\tMS\t\F" << endl;cout << "A\t" << r - 1 << "\t" << S_A << "\t" << S_A/(r - 1) << "\t" << F_A << endl;cout << "B\t" << s - 1 << "\t" << S_B << "\t" << S_B/(s - 1) << "\t" << F_B << endl;cout << "AXB\t" << (r - 1) * (s - 1) << "\t" << S_AB << "\t" << S_AB / ((r - 1) * (s - 1)) << "\t" << F_AB << endl;cout << "error\t" << r * s * (t - 1) << "\t" << S_E << "\t" << S_E/(r * s * (t - 1)) << endl;cout << "total\t" << r * s * t - 1 << "\t" << S_T << endl;return 0;
}
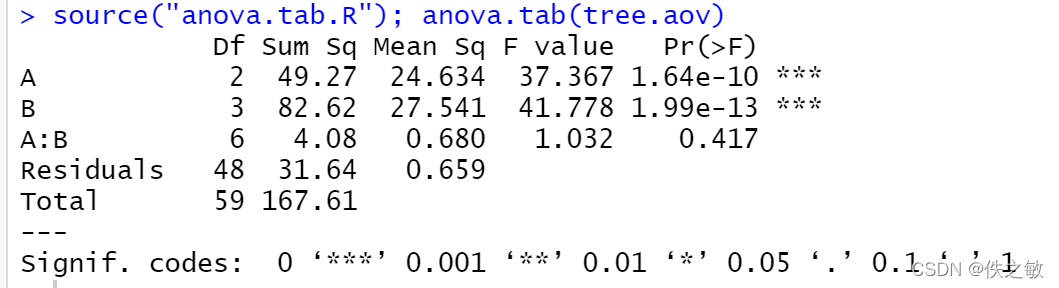
运行结果:
- MATLAB求解
function annova_solve()x = [14, 11, 13, 10;10, 11, 9, 12;9, 10, 7, 6;7, 8, 11, 10;5, 13, 12, 14;11, 14, 13, 10];p = anova2(x,2);
end
运行结果:
- Excel求解
录入数据如下:
在“数据分析”中选择“可重复双因素分析”,选择区域,单击“确定”:
结果如下:
- 结论
查表可知, F 0.05 < F A < F 0.01 F_{0.05}<F_{A}<F_{0.01} F0.05<FA<F0.01, F B , F A × B < F 0.05 F_{B},F_{A\times B}<F_{0.05} FB,FA×B<F0.05。故认为浓度影响较为显著,温度与交互作用影响不显著。
查看原文(我的博客)