双因素方差分析

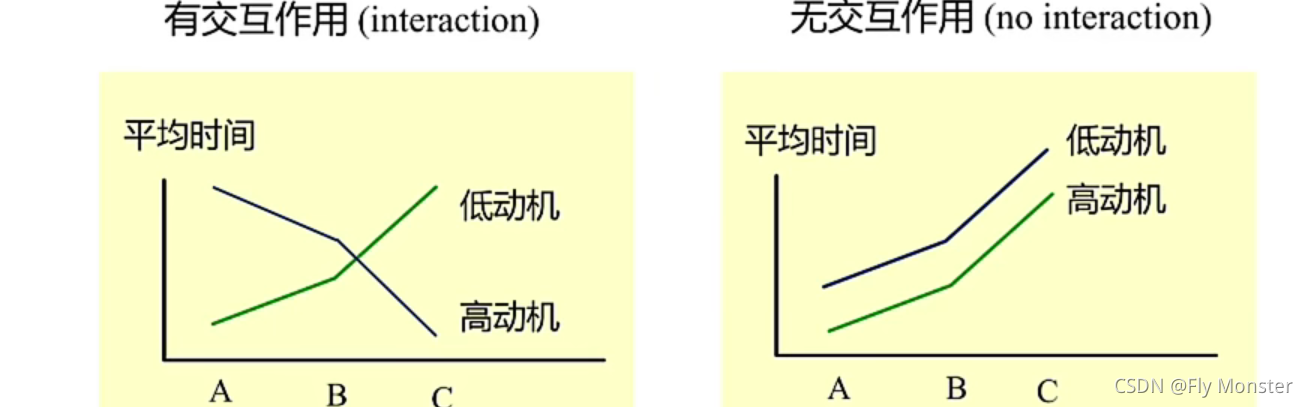
对于两因素的方差分析，基本思想和方法与单因素的方差分析相似，前提条件仍然是要满足独立、正态、方差齐性。所不同的是在双因素方差分析中有时会出现交互作用，即二因素的不同水平交差搭配对指标产生影响。下面先讨论无交互作用的双因素方差分析。

1. 无交互作用的双因素方差分析

例2：考虑三种不同形式的广告和五种不同的价格对某种商品销量的影响。选取某市15家大超市，每家超市选用其中的一个组合，统计出一个月的销量如下（设显著性水平为0.05）：
在这里插入图片描述
在这里对商品销量的影响不仅有广告的影响，还有价格的影响，这就是双因素方差分析。

1.1. 无交叉双因素分析的数学模型

设A，B两个因素，因素A有r个水平 $A_1, A_2, ..., A_r$ ; 因素B有s个水平 $B_1, B_2, ..., B_s$ . 对因素A,B的水平的每队组合（A,B）下进行一次独立实验得到观察值 $X_{ij}, i=1,2,...r, j=1,2,...,s,$ 假定 $_{ij} \sim N(\mu_{ij}, \sigma^2)$ , 且各 $X_{ij}$ 相互独立。则不考虑交互作用的双因素方差分析模型可表示为：
$\begin{cases} X_{ij} = \mu_i + \alpha_i + \varepsilon_{ij}, i=1,2,...,r, j=1,2,...,s, \\ \varepsilon_{ij} \sim N(0, \sigma^2), 且各\varepsilon_{ij}相互独立， \\ \sum_{i=1}^r\alpha_i = 0, \quad \sum_{j=1}^s\beta_j=0 \end{cases}$
其中 $\mu = \frac{1}{rs}\sum_{i=1}^r\sum_{j=1}^s\mu_{ij}$ 为总平均. $\alpha_i$ 为因素A的第 $i$ 个水平的效应， $\beta_j$ 为因素B的第 $j$ 个水平的效应。

在给定显著性水平 $\alpha$ 下，考虑如下假设检验：
$H_{01}:\alpha_1=\alpha_2=...=\alpha_r=0$ (因子A对指标的影响不显著)
$H_{02}:\beta_1=\beta_2=...=\beta_s=0$ (因子B对指标的影响不显著）

类似于单因素方差分析，先对总离差平方和 $SS_T$ 分解为因素A的效应平方和 $SS_A$ ，因素B的效应平方和 $SS_B$ 及误差平方和 $SS_E$ , 即
$SS_T = SS_A+SS_B+SS_E$
可以证明：
1）当 $H_{01}$ 成立时，
$\frac{SS_A}{\sigma^2} \sim \chi^2(r-1), \frac{SS_E}{\sigma^2}\sim \chi^2((r-1)(s-1)),$
而且 $SS_A$ 与 $SS_E$ 独立，于是
$F_A=\frac{SS_A/(r-1)}{SS_E/[(r-1)(s-1)]} \sim F(r-1, (r-1)(s-1))$
2) 当 $H_{02}$ 成立时，
$\frac{SS_B}{\sigma^2} \sim \chi^2(s-1)$
而且 $SS_B$ 与 $SS_E$ 独立，于是
$F_B=\frac{SS_B/(s-1)}{SS_E/[(r-1)(s-1)]}\sim F(s-1, (r-1)(s-1))$
所以， $H_{01}$ 与 $H_{02}$ 的拒绝域分别为
$C_A = \{F_A > F_{1-\alpha}(r-1,(r-1)(s-1))\}$
$C_B = \{F_B > F_{1-\alpha}(s-1, (r-1)(s-1))\}$
咱们知道单因素方差分析的计算量已经够大了，双因素方差分析计算量那就更大了，所以也必须依赖于统计分析软件进行处理，下面的部分讨论Python如何完成相关计算的。

1.2. 双因素方差分析的实现

针对例2中广告和价格对商品销量的影响分析展开计算。
第一步：数据输入

# 导入相关库
import numpy as np
import pandas as pdd = np.array([[276, 352, 178, 295, 273],[114, 176, 102, 155, 128],[364, 547, 288, 392, 378]
])
df = pd.DataFrame(d)
df.index=pd.Index(['A1','A2','A3'],name='ad') 
df.columns=pd.Index(['B1','B2','B3','B4','B5'], name='price')

此时在jupyter notebook下df输入结果如下：
在这里插入图片描述
第二步：数据处理
数据处理的目的就是产生符合模型输入的数据类型，有关pandas数据处理，参考相关文档。

df1 = df.stack().reset_index().rename(columns={0:'value'})
df1

在jupyter notebook下df1输出如下：
在这里插入图片描述
第三步：进行方差分析

from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lmmodel = ols('value~C(ad) + C(price)', df1).fit()
anova_lm(model)

上述代码中ols的作用就是从一个公式和数据框创建一个模型。这里的公式语法就是由Patsy库提供支持的，C函数完成分类变量转换。
anova_lm就是为模型产生一个方差分析表。

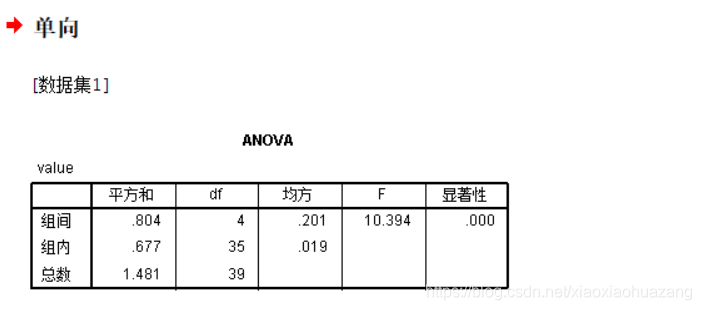
在jupyer notebook下产生的输出如下：
在这里插入图片描述
第四步：结果分析和决策建议
对广告因素来说，因为其 $p = 0.000013$ 小于显著性水平 $\alpha=0.05$ ,因此拒绝原假设，有理由相信广告对商品的销量是有影响的。
对价格因素来说，同样因为其 $p = 0.005833$ 小于显著性水平 $\alpha=0.05$ ,因此也拒绝原假设，有理由相信对商品销量也是有影响的。

2. 有交互作用的双因素方差分析

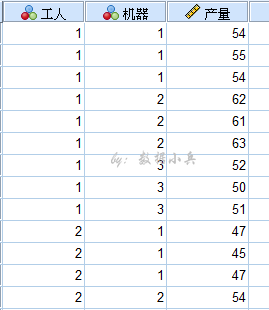
例3：火箭的射程与燃料的种类和推进器的型号有关，现对四种不同的燃料与三种不同型号的推进器进行试验，每种组合各发射火箭两次，测得火箭的射程结果如下（设显著性水平为0.01）：
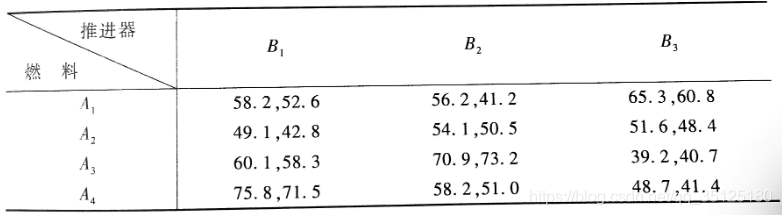
在这里插入图片描述
这里火箭的射程不仅受到燃料类型和推进器型号的影响，同时还受到二者交互作用。这就好比两个好朋友甲和乙，甲的酒量也就半斤，儿乙的酒量有八两，但是两个好朋友聚到一起，把酒言欢结果一下喝掉了2斤多酒，哈哈哈。

2.1. 数学模型

设有两个因素A和B, 因素A有r个水平 $A_1 ,A_2 , ... ,A_r$ ; 因素B有s个水平 $B_1, B_2,...,B_s$ . 在许多情况下, 两因素A与B之间存在着一定程度的交互作用. 为了考察因素间的交互作用, 要求在两个因素的每一水平组合下进行重复试验. 设在每种水平组合 $A_i, B_j)$ 下重复试验t次. 记第k次的观测值为 $X_{ijk}$ .则有交互作用的两因素方差分析模型可表示为
$\begin{cases} X_{ij} = \mu + \alpha_i + \beta_j + \delta_{ij} + \varepsilon_{ijk}, i=1,2,...,r, j=1,2,...,s, k=1,2,...,t \\ \varepsilon_{ijk} \sim N(0, \sigma^2), 且各\varepsilon_{ijk}相互独立 \\ \sum_{i=1}^r\alpha_i=0, \sum_{j=1}^s\beta_j=0, \sum_{i=1}^s\delta_{ij}=\sum_{j=1}^s\delta_{ij}=0 \end{cases}$
这里 $\alpha_i$ 为因素A的第 $i$ 个水平的效应， $\beta_j$ 为因素B的第 $j$ 个水平的效应， $\delta_{ij}为A_i和B_j的交互效应， \mu=\frac{1}{rs}\sum_{i=1}^r\sum_{j=1}^s\mu_{ij}.$

检验的假设为：
$H_{01}: \alpha_1 = \alpha_2 =... = \alpha_r = 0 （因素A对指标没有影响）\\ H_{02}: \beta_1 = \beta_2 = ... = \beta_s = 0 （因素B对指标没有影响） \\ H_{03}: \delta_{11} = \delta_{12} = ... = \delta_{rs} = 0 （因素A和B没有联合作用）$
类似于无交互作用的方差分析, 总的离差平方和可分解为
$SS_T = SS_E + SS_A + SS_B + SS_{A \times B}$

同时可以证明：
1）当 $H_{01}$ 成立时，
$F_A=\frac{SS_A/(r-1)}{SS_E/[rs(t-1)]} \sim F(r-1, rs(t-1))$
2) 当 $H_{02}$ 成立时，
$F_B=\frac{SS_B/(s-1)}{SS_E/[rs(t-1)]} \sim F(s-1, rs(t-1))$
3) 当 $H_{03}$ 成立时，
$F_{A\times B}=\frac{SS_{A\times B}/[(r-1)(s-1)]}{SS_E/[rs(t-1)]} \sim F((r-1)(s-1), rs(t-1))$

2. 2. 有交互作用的方差分析的实现

针对例3展开计算。
步骤一：输入数据

import numpy as np
import pandas as pd d = np.array([[58.2, 52.6, 56.2, 41.2, 65.3, 60.8],[49.1, 42.8, 54.1, 50.5, 51.6, 48.4],[60.1, 58.3, 70.9, 73.2, 39.2, 40.7],[75.8, 71.5, 58.2, 51.0, 48.7,41.4]
])
df = pd.DataFrame(d)
df.index=pd.Index(['A1','A2','A3','A4'],name='燃料')
df.columns=pd.Index(['B1','B1','B2','B2','B3','B3'],name='推进器')
df

在jupyter notebook下df输出如下：
在这里插入图片描述

第二步：数据处理

df1 = df.stack().reset_index().rename(columns={0:'射程'})
df1

在jupyter notebook下df1的输出如下：
在这里插入图片描述

第三步：数据分析

from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lmmodel = ols('射程~C(燃料) + C(推进器)+C(燃料):C(推进器)', df1).fit()
anova_lm(model)

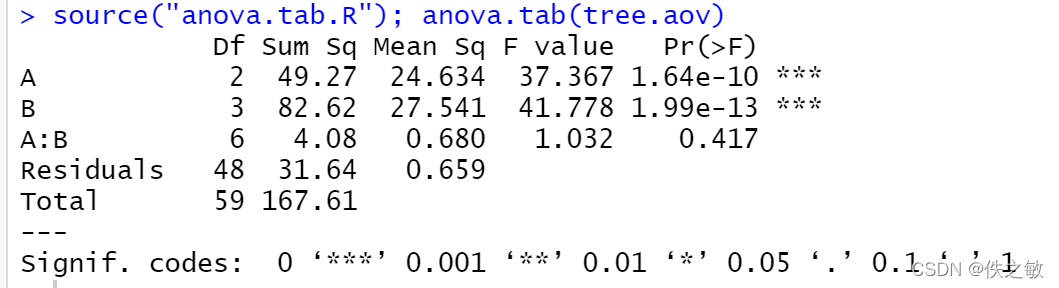
在jupyter notebook下输出的方差分析表如下：
在这里插入图片描述
第四步：结果分析和决策建议
对燃料因素来说，其 $p = 0.025$ 大于显著性水平 $\alpha=0.01$ . 所以其对射程没有影响；
对推进器因素来说，其 $p = 0.003506$ 小于显著水平 $\alpha=0.01$ , 所以其对射程影响显著。
对燃料和推进器的交互因素来说，其 $p = 0.000062$ 小于显著水平 $\alpha=0.01$ ，所以其对射程影响显著。