理论依据
【基本思想】
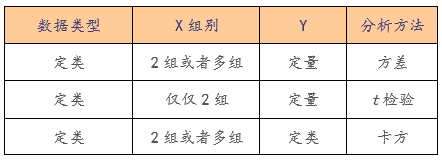
方差分析是检验两个或两个以上的样本均值之间的差异是否具有统计学意义的一种方法,目的是推断两个或两个以上的总体均值是否相同。它所研究的是分类型自变量对数值型因变量的影响。当只涉及一个分类型自变量时,该分析称为单因素方差分析;涉及两个或两个以上的分类型自变量时,则称为多因素方差分析。
通过比较多总体均值来研究自变量与因变量的关系是否显著。
方差分析认为,观测变量的变动会受到因素变量和随机变量两方面的影响。观测变量的总变动用总离差平方和(SST)表示,将其分解为组间离差平方和(SSB)和组内离差平方和(SSE)。其中,SSB由于因素变量的不同水平而引起的观测变量的变动(也称系统误差);SSE是由于随机因素而引起的观测变量的变动。
1.单因素方差分析的理论假设:
(1)各处理下的样本是随机的。
(2)各处理下的样本是相互独立的。
(3)各处理下的样本分别来自服从正态分布的总体。
(4)各处理下的样本所属总体的方差相等。
2.单因素方差分析的基本步骤:
(1)建立假设;
(2)计算样本均值;
(3)计算总样本均值;
(4)计算样本方差;
(5)计算总体方差的组间估计;
(6)计算总体方差的组内估计;
(7)给定显著性水平α;
(8)计算F统计量的值;
(9)编制方差分析表。
(10)做出统计决策。
3.单因素方差中的多重比较
如果经过上述步骤推断总体均值之间存在显著差异,接下来的问题就是确定自变量的不同水平对因变量的影响程度如何,其中哪些水平的作用明显区别于其他水平,哪些水平的作用不显著。这就要用到多重比较的分析方法。
多重比较是利用样本数据,对各个水平下的总体均值逐一进行两两之间的比较检验。由于所采用的检验统计量不同,多重比较有许多具体方法,最常用的是最小显著性差异法(LSD法),检验的统计量是一个t统计量。计算t统计量公式为:
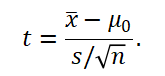
【实验目的】
1.掌握单因素方差分析的基本理论和基本步骤。
2.熟练掌握单因素方差分析的SPSS操作。
3.能够利用单因素方差分析工具解决身边的实际问题。
实验内容
某企业新开发了一批商品,为了解不同的促销方式,有无售后服务,对此产品的销售是否有影响,该企业在城市中随机抽取了24个规模、地理位置等条件相似的超市进行实验。其中随机抽取八个超市,采用主动促销的方式在此8个超市中,再随机抽取四个超市给该商品提供售后服务,其余四个超市不提供售后服务,另随机抽取八个超市采用被动促销方式,在此八个超市中再随机抽取四个超市给该商品提供售后服务,其余四个超市不提供售后服务,剩余八个超市不采取促销方式,在此八个超市中再随机抽取四个超市给该商品提供售后服务,其余四个超市不提供售后服务,经过三个月之后再来统计这24个超市销售此商品的销售额,从而获得到了第一手的数据资料。该数据资料包含促销方式,售后服务,销售额三个变量的24个观测。其中,促销方式与售后服务为定类变量,促销方式取值为0=无促销,1=被动促销,2=主动促销,售后服务取值为0=无售后服务,1=有售后服务。数据见Data10-1。
企业拿到这个实验数据之后,想确认促销方式对该商品的销售额是否有显著影响,如果有显著影响,又是哪几种促销方式之间的销售额具有显着性差异。
操作步骤
单因素方差分析
1)打开数据集“data10-1. sav”,选择菜单:【Analyze】→【Compare Means】→【One-Way ANOVA】。
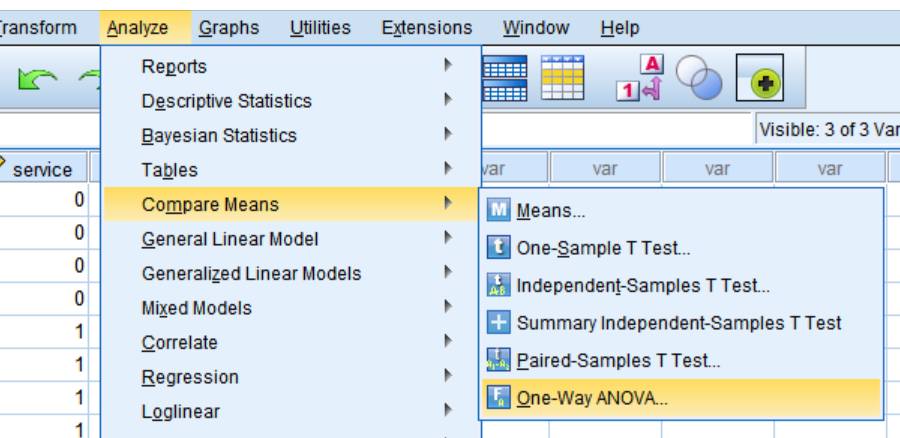
图2-1:选择菜单步骤
2)弹出如图2-2所示的“One-Way ANOVA”对话框。在此对话框中,选择销售额[sales]进入“Dependent List”框中;选择促销方式[promot]进入“Factor”框中。
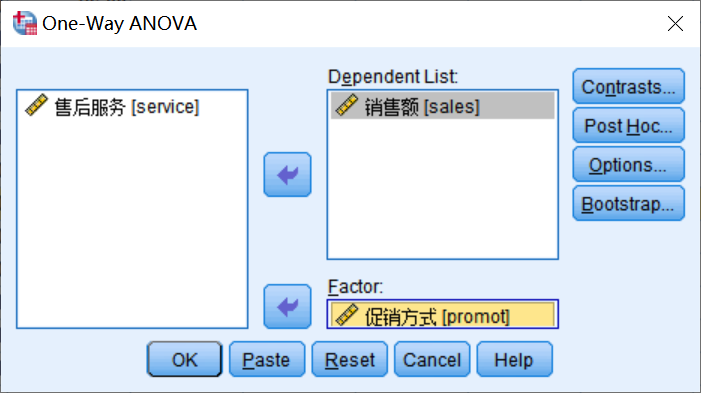
图2-2:“One-Way ANOVA”对话框
3)单击“Options”按钮,弹出如图2-3所示的对话框,在此对话框中选择“Homogeneity of variance test”选项。

图2-3:“Options”对话框
4)点击【Continue】→【OK】,系统输出单因素方差分析的结果如表2-1所示。
表2-1:方差同质性检验输出结果
Test of Homogeneity of Variances | |||||
| Levene Statistic | df1 | df2 | Sig. | |
销售额 | Based on Mean | 5.546 | 2 | 21 | .012 |
Based on Median | 5.301 | 2 | 21 | .014 | |
Based on Median and with adjusted df | 5.301 | 2 | 19.389 | .015 | |
Based on trimmed mean | 5.545 | 2 | 21 | .012 | |
表2-2:方差分析输出结果
ANOVA | |||||
销售额 | |||||
| Sum of Squares | df | Mean Square | F | Sig. |
Between Groups | 579.250 | 2 | 289.625 | 6.406 | .007 |
Within Groups | 949.375 | 21 | 45.208 |
|
|
Total | 1528.625 | 23 |
|
|
|
5)观察分析输出结果
单因素方差分析的结果只能说明3种促销方式对销售额的影响是有差异的,但不能给出各种促销方式两两之间的差异情况。因此,要进一步确定到底哪几种促销方式之间存在差异。这需要进行多重比较检验。具体步骤如下:
进行多重比较
在“One-Way ANOVA”主对话框中点击“Post Hoc”按钮,弹出如图2-4所示的“One-Way ANOVA:Post Hoc Multiple Comparisons”对话框。在此对话框中选择“LSD”选项。
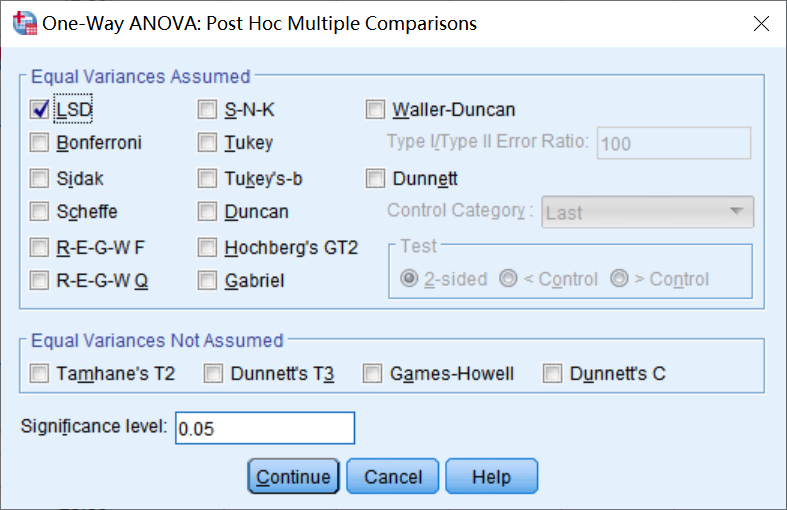
图2-4:“Post Hoc”对话框
2)点击【Continue】→【OK】,系统输出多重比较检验的结果如下文所示。
做出统计决策
输出结果中两两给出了均值差及其对应的P值,在给定的显著性水平下,可得出多重比较的结论。
结果分析
表2-1中给出了方差同质性检验结果,基于平均值来看,因为P值为0.012 < 0.05,所以认为各组的方差不等,即不满足方差齐性这一条件;基于中位数来看,因为P值为0.014 < 0.05,所以认为各组的方差不等,即不满足方差齐性这一条件;基于中位数和调整后的 df来看,因为P值为0.015 < 0.05,所以认为各组的方差不等,即不满足方差齐性这一条件;基于截尾平均值来看,因为P值为0.012 < 0.05,所以认为各组的方差不等,即不满足方差齐性这一条件。
表2-1:方差同质性检验输出结果
Test of Homogeneity of Variances | |||||
| Levene Statistic | df1 | df2 | Sig. | |
销售额 | Based on Mean | 5.546 | 2 | 21 | .012 |
Based on Median | 5.301 | 2 | 21 | .014 | |
Based on Median and with adjusted df | 5.301 | 2 | 19.389 | .015 | |
Based on trimmed mean | 5.545 | 2 | 21 | .012 | |
下表中给出了促销方式的单因素方差分析表,这张表是单因素方差分析的核心。其中,总离差平方和(SSR)为1528.625 = 组间离差平方和(SSB)579.250 + 组内离差平方和(SSE)949.375。SSB中可以被先行解释的部分为564.06,F检验的统计量观察值为6.406,对应P值为0.007 < 0.05,因此,三种促销方式中至少有一组与另外一组存在显著差异。
表2-2:方差分析输出结果
ANOVA | |||||
销售额 | |||||
| Sum of Squares | df | Mean Square | F | Sig. |
Between Groups | 579.250 | 2 | 289.625 | 6.406 | .007 |
Within Groups | 949.375 | 21 | 45.208 |
|
|
Total | 1528.625 | 23 |
|
|
|
表2-3中给出了多重比较的结果,从表中可以看出,无促销方式与主动促销、被动促销与主动促销的显著性分别为0.002、0.034,均小于0.05,说明这几组之间的差异显著,而无促销方式与被动促销之间的显著性为0.220 > 0.05,说明差异不显著。
表2-3:多重比较输出结果
Multiple Comparisons | ||||||
Dependent Variable: 销售额 | ||||||
LSD | ||||||
(I) 促销方式 | (J) 促销方式 | Mean Difference (I-J) | Std. Error | Sig. | 95% Confidence Interval | |
Lower Bound | Upper Bound | |||||
无 | 被动促销 | -4.25000 | 3.36186 | .220 | -11.2414 | 2.7414 |
主动促销 | -11.87500* | 3.36186 | .002 | -18.8664 | -4.8836 | |
被动促销 | 无 | 4.25000 | 3.36186 | .220 | -2.7414 | 11.2414 |
主动促销 | -7.62500* | 3.36186 | .034 | -14.6164 | -.6336 | |
主动促销 | 无 | 11.87500* | 3.36186 | .002 | 4.8836 | 18.8664 |
被动促销 | 7.62500* | 3.36186 | .034 | .6336 | 14.6164 | |
*. The mean difference is significant at the 0.05 level. | ||||||