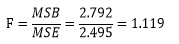1.基本概念
- 试验指标:在试验中要考察的指标,如产品质量等。
- 因素:影响试验指标的条件。包括可控因素和不可控因素。
- 单因素试验:在一项试验中只有一个因素在改变的试验。
- 多因素试验:在一项试验中多于一个因素在改变的试验。
- 水平:因素所处的状态。
- 随机误差:同一水平下,样本各观察值之间的差异,称为随机误差。这种差异可以看成是随机因素的影响。
- 系统误差:不同水平下,各观察值之间的差异。这种差异可能是由于行业本身所造成的,称为系统误差。
2.方差分析的任务
- 检验 s s s个总体 N ( μ 1 , σ 2 ) , . . . , N ( μ s , σ 2 ) N(\mu_1,\sigma^2),...,N(\mu_s,\sigma^2) N(μ1,σ2),...,N(μs,σ2)的均值是否相等,即检验假设:
H 0 : μ 1 = μ 2 = . . . = μ s H 1 : μ 1 , μ 2 , . . . , μ s 不 全 相 等 H_0:\mu_1=\mu_2=...=\mu_s\\ H_1:\mu_1,\mu_2,...,\mu_s不全相等 H0:μ1=μ2=...=μsH1:μ1,μ2,...,μs不全相等
- 作出未知参数 μ 1 , μ 2 , . . . , μ s , σ 2 \mu_1,\mu_2,...,\mu_s,\sigma^2 μ1,μ2,...,μs,σ2的估计
总平均:
μ = 1 n ∑ j = 1 s n j μ j n = ∑ j = 1 s n j \mu=\frac{1}{n}\sum_{j=1}^{s}n_j\mu_j\\ n=\sum_{j=1}^{s}n_j μ=n1j=1∑snjμjn=j=1∑snj
A j A_j Aj下总体平均值与总平均值的差异:
δ j = μ j = μ , j = 1 , 2 , . . . , s X i j = μ j + ϵ i j , ϵ i j N ( 0 , σ 2 ) 各 ϵ i j 独 立 , i = 1 , 2 , . . . , n j , j = 1 , 2 , . . . , s ⇓ X i j = μ + σ j + ϵ i j , ϵ i j N ( 0 , σ 2 ) . 各 ϵ i j 独 立 i = 1 , 2 , . . . , n j , j = 1 , 2 , . . . , s , ∑ j = 1 s n j δ j = 0 \delta_j=\mu_j=\mu,\space\space j=1,2,...,s \\ X_{ij}=\mu_j+\epsilon_{ij},\space\epsilon_{ij}~N(0,\sigma^2)\\ 各\epsilon_{ij}独立,\space i=1,2,...,n_j,\space j=1,2,...,s\\ \Downarrow\\ X_{ij}=\mu+\sigma_j+\epsilon_{ij},\space\epsilon_{ij}~N(0,\sigma^2).\space 各\epsilon_{ij}独立\\ i=1,2,...,n_j,\space j=1,2,...,s,\space\sum_{j=1}^{s}n_j\delta_j=0\\ δj=μj=μ, j=1,2,...,sXij=μj+ϵij, ϵij N(0,σ2)各ϵij独立, i=1,2,...,nj, j=1,2,...,s⇓Xij=μ+σj+ϵij, ϵij N(0,σ2). 各ϵij独立i=1,2,...,nj, j=1,2,...,s, j=1∑snjδj=0
因为 μ 1 = μ 2 = . . . = μ s \mu_1=\mu_2=...=\mu_s μ1=μ2=...=μs时:
μ = 1 n ∑ j = 1 s n j μ j = 1 n μ j ∑ j = 1 s n j = 1 n μ j n = μ j δ j = μ j − μ , j = 1 , 2 , . . . , s \mu=\frac{1}{n}\sum_{j=1}^{s}n_j\mu_j=\frac{1}{n}\mu_j\sum_{j=1}^{s}n_j=\frac{1}{n}\mu_j n=\mu_j\\ \delta_j=\mu_j-\mu,\space j=1,2,...,s μ=n1j=1∑snjμj=n1μjj=1∑snj=n1μjn=μjδj=μj−μ, j=1,2,...,s
所以:
H 0 : μ 1 = μ 2 = . . . = μ s H 1 : μ 1 , μ 2 , . . . , μ s 不 全 相 等 ⇓ H 0 : δ 1 = δ 2 = . . . = δ s H 1 : δ 1 , δ 2 , . . . , δ s 不 全 为 零 H_0:\mu_1=\mu_2=...=\mu_s\\ H_1:\mu_1,\mu_2,...,\mu_s不全相等\\ \Downarrow\\ H_0:\delta_1=\delta_2=...=\delta_s\\ H_1:\delta_1,\delta_2,...,\delta_s不全为零 H0:μ1=μ2=...=μsH1:μ1,μ2,...,μs不全相等⇓H0:δ1=δ2=...=δsH1:δ1,δ2,...,δs不全为零
3.平方和的分解
| A 1 A_1 A1 | A 2 A_2 A2 | … | A s A_s As |
|---|---|---|---|
| X 11 X_{11} X11 | X 12 X_{12} X12 | … | X 1 s X_{1s} X1s |
| X 21 X_{21} X21 | X 22 X_{22} X22 | … | X 2 s X_{2s} X2s |
| … | … | … | … |
| X n 1 1 X_{n_1 1} Xn11 | X n 2 2 X_{n_2 2} Xn22 | … | X n s s X_{n_s s} Xnss |
记 X ˉ ⋅ j = 1 n j ∑ i = 1 n j X i j \bar{X}_{\cdot j}=\frac{1}{n_{j}} \sum_{i=1}^{n_{j}} X_{i j} Xˉ⋅j=nj1∑i=1njXij
水平 A i A_i Ai下的样本均值(总的样本均值):
X ˉ = 1 n ∑ i = 1 s ∑ j = 1 n i X i j \bar{X}=\frac{1}{n} \sum_{i=1}^{s} \sum_{j=1}^{n_{i}} X_{i j} Xˉ=n1i=1∑sj=1∑niXij
总偏差平方和(总变差,反映了全部试验数据之间的差异):
S T = ∑ j = 1 s ∑ i = 1 n j ( X i j − X ˉ ) 2 S_{T}=\sum_{j=1}^{s} \sum_{i=1}^{n_{j}}\left(X_{i j}-\bar{X}\right)^{2} ST=j=1∑si=1∑nj(Xij−Xˉ)2
组内偏差平方和(误差平方和,反映了水平 A i A_i Ai内有随机误差二引起的波动):
S e = ∑ j = 1 s ∑ i = 1 n j ( X i j − X ˉ ⋅ j ) 2 S_{e}=\sum_{j=1}^{s} \sum_{i=1}^{n_{j}}\left(X_{i j}-\bar{X}_{\cdot j}\right)^{2} Se=j=1∑si=1∑nj(Xij−Xˉ⋅j)2
组间偏差平方和(效应平方和,由水平 A j A_j Aj的效应的差异以及随机误差引起):
S A = ∑ j = 1 s n j ( X . j − X ˉ ) 2 S_{A}=\sum_{j=1}^{s} n_{j}\left(X_{. j}-\bar{X}\right)^{2} SA=j=1∑snj(X.j−Xˉ)2
总离差平方和分解式:
S T = S e + S A S_{T}=S_{e}+S_{A} ST=Se+SA
4. S e , S A S_e,S_A Se,SA的统计特性
- S e S_e Se的统计特性
S e = ∑ i = 1 n 1 ( X i 1 − X ˉ ⋅ 1 ) 2 + ⋯ + ∑ i = 1 n s ( X i s − X ˉ ⋅ s ) 2 S_{e}=\sum_{i=1}^{n_{1}}\left(X_{i 1}-\bar{X}_{\cdot 1}\right)^{2}+\cdots+\sum_{i=1}^{n_{s}}\left(X_{i s}-\bar{X}_{\cdot s}\right)^{2} Se=i=1∑n1(Xi1−Xˉ⋅1)2+⋯+i=1∑ns(Xis−Xˉ⋅s)2
∑ i = 1 n j ( X i j − X ˉ . j ) 2 \sum_{i=1}^{n_{j}}\left(X_{i j}-\bar{X}_{. j}\right)^{2} ∑i=1nj(Xij−Xˉ.j)2是总体 N ( μ j , σ 2 ) N\left(\mu_{j}, \sigma^{2}\right) N(μj,σ2)的样本方差的 n j − 1 n_{j}-1 nj−1倍,
∑ i = 1 n j ( X i j − X ˉ . j ) 2 σ 2 ∼ χ 2 ( n j − 1 ) \frac{\sum_{i=1}^{n_{j}}\left(X_{i j}-\bar{X}_{. j}\right)^{2}}{\sigma^{2}} \sim \chi^{2}\left(n_{j}-1\right) σ2∑i=1nj(Xij−Xˉ.j)2∼χ2(nj−1)
由 χ 2 \chi^2 χ2分布的可加性:
S E σ 2 ∼ χ 2 ( ∑ j = 1 s ( n j − 1 ) ) \frac{S_{E}}{\sigma^{2}} \sim \chi^{2}\left(\sum_{j=1}^{s}\left(n_{j}-1\right)\right) σ2SE∼χ2(j=1∑s(nj−1))
即:
S E σ 2 ∼ χ 2 ( n − s ) , E ( S E ) = ( n − s ) σ 2 \frac{S_{E}}{\sigma^{2}} \sim \chi^{2}(n-s), \quad E\left(S_{E}\right)=(n-s) \sigma^{2} σ2SE∼χ2(n−s),E(SE)=(n−s)σ2
- S A S_A SA的统计特性
E ( S A ) = ( s − 1 ) σ 2 + ∑ j = 1 s n j δ 2 E\left(S_{A}\right)=(s-1) \sigma^{2}+\sum_{j=1}^{s} n_j \delta^{2} E(SA)=(s−1)σ2+j=1∑snjδ2
且当 H 0 H_0 H0为真时:
S A σ 2 ∼ χ 2 ( s − 1 ) \frac{S_{A}}{\sigma^{2}} \sim \chi^{2}(s-1) σ2SA∼χ2(s−1)
5.拒绝域
- F F F比
定义 F F F比:
F = S A ˉ S e ˉ = S A / ( S − 1 ) S E / ( n − s ) F=\frac{\bar{S_A}}{\bar{S_e}}=\frac{S_A/\left(S-1\right)}{S_E/\left(n-s\right)} F=SeˉSAˉ=SE/(n−s)SA/(S−1)
故检验问题拒绝域具有形式:
F = S A / ( S − 1 ) S E / ( n − s ) ≤ k F=\frac{S_A/\left(S-1\right)}{S_E/\left(n-s\right)}\le k F=SE/(n−s)SA/(S−1)≤k
其中 k k k由显著性水平 α \alpha α决定。
- 方差分析表
| 方差来源 | 平方和 | 自由度 | 均方 | F F F比 |
|---|---|---|---|---|
| 因素 A A A | S A S_A SA | s − 1 s-1 s−1 | S ‾ A = S A s − 1 \overline{S}_{A}=\frac{S_{A}}{s-1} SA=s−1SA | F = S ‾ A S ‾ E F=\frac{\overline{\boldsymbol{S}}_{\boldsymbol{A}}}{\overline{\boldsymbol{S}}_{\boldsymbol{E}}} F=SESA |
| 误差 | S E S_E SE | n − s n-s n−s | S ˉ E = S E n − s \bar{S}_{E}=\frac{S_{E}}{n-s} SˉE=n−sSE | |
| 总和 | S T S_T ST | n − 1 n-1 n−1 |
6.单因素方差分析的实现
- 例题
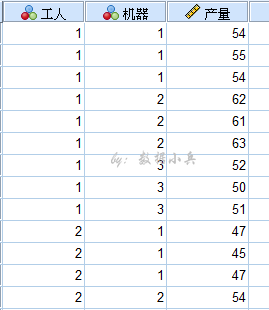
工程师测量了四种不同类型外壳的彩色显像管的传导率,得传导率的观察值如下表:
| 显像管型号 | 传导率值1 | 传导率值2 | 传导率值3 | 传导率值4 |
|---|---|---|---|---|
| A 1 A_1 A1(类型1) | 143 | 141 | 150 | 146 |
| A 2 A_2 A2(类型2) | 152 | 144 | 137 | 143 |
| A 3 A_3 A3(类型3) | 134 | 136 | 133 | 129 |
| A 4 A_4 A4(类型4) | 129 | 128 | 134 | 129 |
问: 外壳类型对传导率是否由显著影响? ( α = 0.05 \alpha=0.05 α=0.05)
- 作出假设
设水平 A i A_i Ai下, X i ∼ N ( a i , σ 2 ) X_{i} \sim N\left(a_{i}, \sigma^{2}\right) Xi∼N(ai,σ2)。
假设 H 0 : a 1 = a 2 = a 3 = a 4 H_{0}: a_{1}=a_{2}=a_{3}=a_{4} H0:a1=a2=a3=a4; H 1 : a 1 , a 2 , a 3 , a 4 H_{1}: a_{1},a_{2},a_{3},a_{4} H1:a1,a2,a3,a4不全相等。 - Excel求解
录入数据至Excel表格:
点击“数据”-“数据分析”-“单因素方差分析”(需要加载数据分析库)
选中数据区域。由于该表中每行为一种类型,故选择行分组方式,依题意, α ( A ) \alpha(A) α(A)取0.05,单击“确定”:
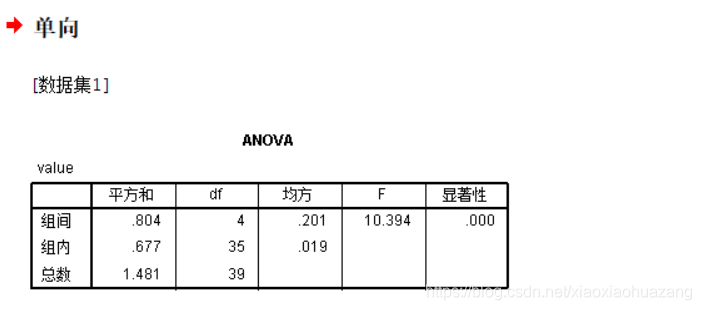
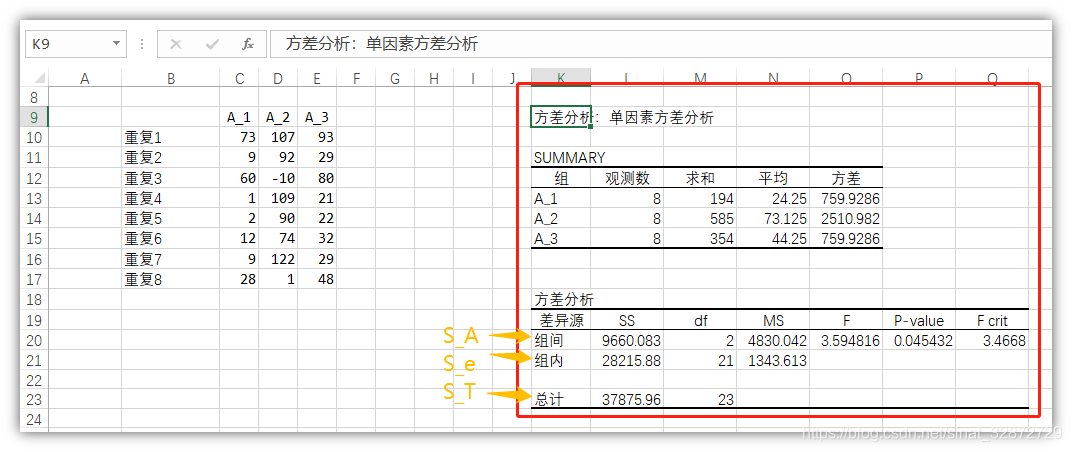
可在新工作表中看见方差分析表:
- matlab求解
%solve20200308.m
function solve20200308()x = [143, 152, 134, 129;141, 144, 136, 128;150, 137, 133, 134;146, 143, 129, 129];p = anova1(x)
end
%控制台键入
solve20200308()
方差分析表:
- python求解
import pandas as pd
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lmdf = pd.read_csv('D:\Data\ex_5.csv')
print(df)
model = ols('conductivity~type', data = df).fit()
table = anova_lm(model)
print(table)
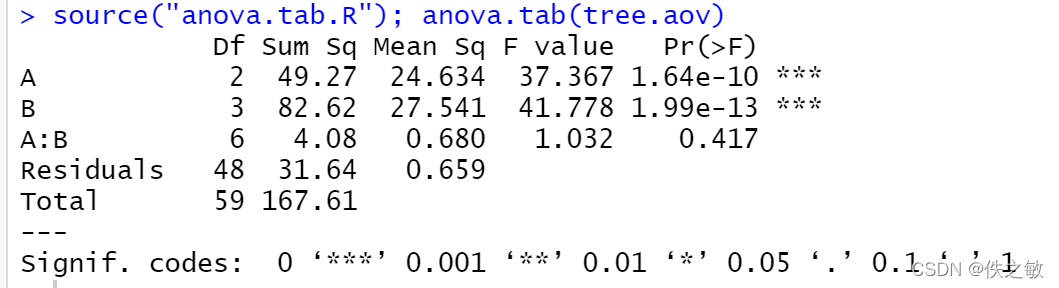
运行结果:
- 结论
由于 F > 3.49 F>3.49 F>3.49,拒绝 H 0 H_0 H0,认为外壳类型对传导率影响显著。
原文链接: https://blog.tigerxly.com/?p=1339 (本人博客)