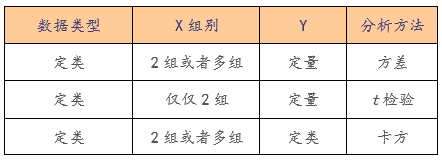
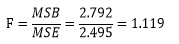假定实验或观察中只有一个因素(因子)A(比如说试剂浓度),有m个水平。各在每一种水平下,做n次实验。 X i j X_{ij} Xij表示第j个水平下的第i次实验。
| 实验次数 | A1水平 | A2水平 | … | Am水平 |
|---|---|---|---|---|
| 1 | X 11 X_{11} X11 | X 12 X_{12} X12 | … | X 1 m X_{1m} X1m |
| 2 | X 21 X_{21} X21 | X 22 X_{22} X22 | … | X 2 m X_{2m} X2m |
| … | … | … | … | … |
| i | X i 1 X_{i1} Xi1 | X i 2 X_{i2} Xi2 | … | X i m X_{im} Xim |
| … | … | … | … | … |
| n | X n 1 X_{n1} Xn1 | X n 2 X_{n2} Xn2 | … | X n m X_{nm} Xnm |
为了考察因素A对实验结果是否有显著性影响,即看各个水平之间实验结果均值的差异。把因素A的m个水平看成是m个正态总体, X ∼ N ( a j , σ 2 ) X\sim N(a_{j},\sigma^2) X∼N(aj,σ2), j = 1... m j=1...m j=1...m, a j a_{j} aj表示第j个总体的总体均值。 a j = μ + ξ j a_{j} =\mu + \xi _{j} aj=μ+ξj, ξ j \xi _{j} ξj是第j个水平相对于nm个全体数据总体均值的偏差。
- 想要知道各个水平之间是否有差异,相当于检验零假设
H 0 = a 1 = a 2 = . . . = a j = . . . = a m = μ H_{0}=a_{1}=a_{2}=...=a_{j}=...=a_{m}=\mu H0=a1=a2=...=aj=...=am=μ
H 0 = ξ 1 = ξ 2 = . . . = ξ j = . . . = ξ m = 0 H{0}=\xi_{1}=\xi_{2}=...=\xi_{j}=...=\xi_{m}=0 H0=ξ1=ξ2=...=ξj=...=ξm=0
- 计算各水平均值
令 x j ‾ \overline{x_{j}} xj表示第j种水平的样本均值。 - 计算离差平方和
- 总离差平方和(SST):所有数据观测值与全部数据均值的平方和。自由度n-1
S S T = ∑ ∑ ( x i j − x ‾ ) 2 SST=\sum\sum(x_{ij} -\overline{x})^2 SST=∑∑(xij−x)2 - 组内平方和(SSE):先计算各水平内数据与组内均值之差的平方和,再将各水平计算结果累计。反映了组内观察值的离散状况,即随机因素的影响。自由度n-m
S S E = ∑ j [ ∑ i ( x i j − x j ‾ ) 2 ] SSE=\sum_{j}[\sum_{i}(x_{ij}-\overline{x_{j}})^2] SSE=∑j[∑i(xij−xj)2]
平均平方 M S E = S S E n − m MSE=\frac{SSE}{n-m} MSE=n−mSSE - 组间平方和(SSA):组内均值与总体均值之差的平方,乘以观察值个数。再累加各组计算值。表现得是组间差异,包含随机因素,也包括系统因素。自由度m-1
S S A = ∑ m [ n j ( x ‾ j − x ‾ ) 2 ] SSA=\sum_{m}[n_{j}(\overline x_{j}-\overline x)^2] SSA=∑m[nj(xj−x)2]
平均平方: M S A = S S A m − 1 MSA=\frac{SSA}{m-1} MSA=m−1SSA - S S T = S S E + S S A SST=SSE+SSA SST=SSE+SSA
- 总离差平方和(SST):所有数据观测值与全部数据均值的平方和。自由度n-1
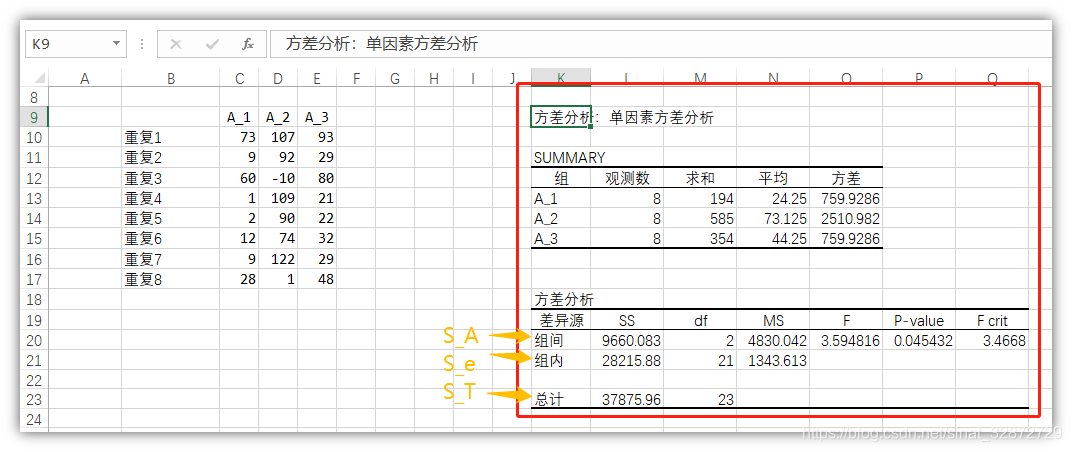
- 方差分析
统计量F: F = 组 间 方 差 组 内 方 差 = M S A M S E F=\frac{组间方差}{组内方差}=\frac{MSA}{MSE} F=组内方差组间方差=MSEMSA
统计量计算结果相当于p值。

- 做统计判断
对于给定显著性水平 α \alpha α,由F分布表查出自由度(m-1,n-m)的临界值 F α F_{\alpha} Fα
如果 F > F α F>F_{\alpha} F>Fα,则拒绝原假设。原假设是各水平之间无差异,所以得出各水平之间的结果由显著的差异。
反之,接受原假设,不同水平之间结果差异不显著。