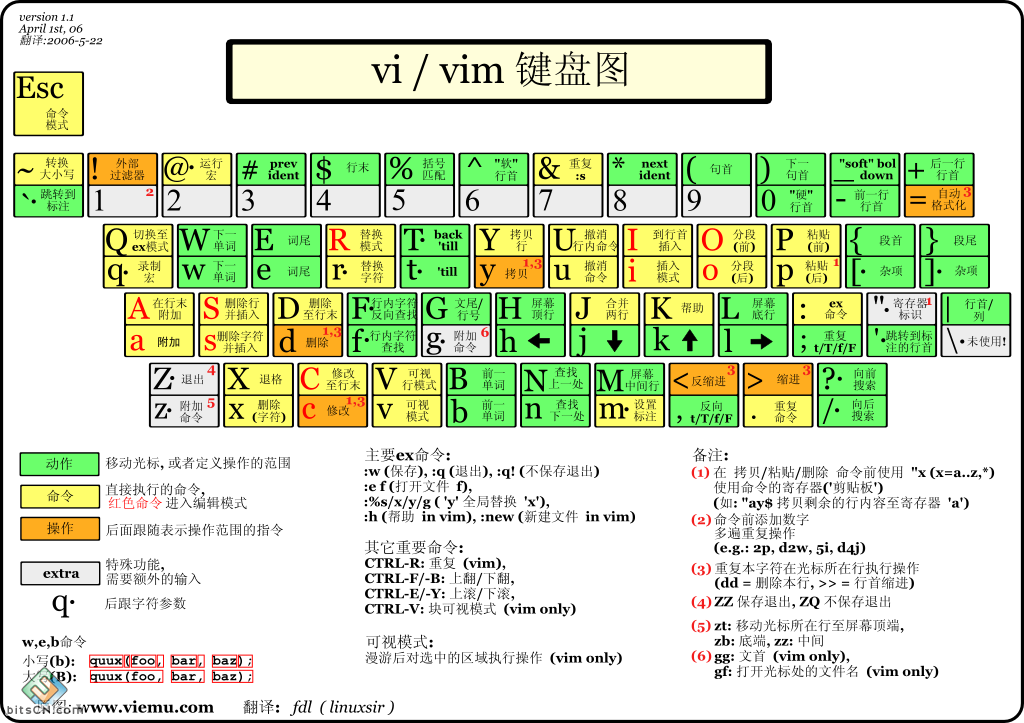
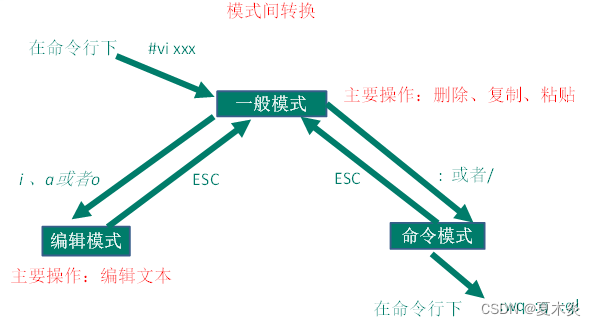
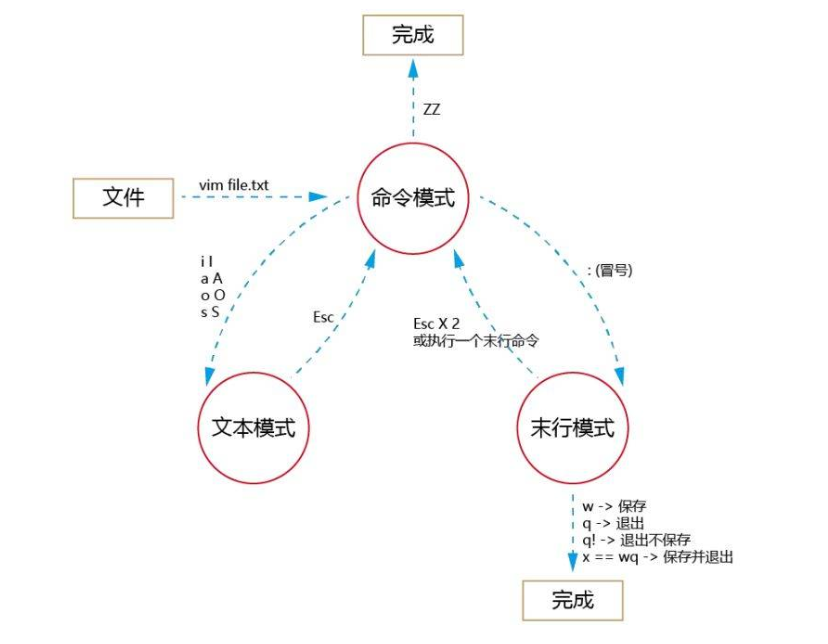
单因素方差分析的应用
- 前言
- 概念:
- 使用要求:
- 基本思想:
- 计算原理:
- 分析步骤:
- 例题
前言
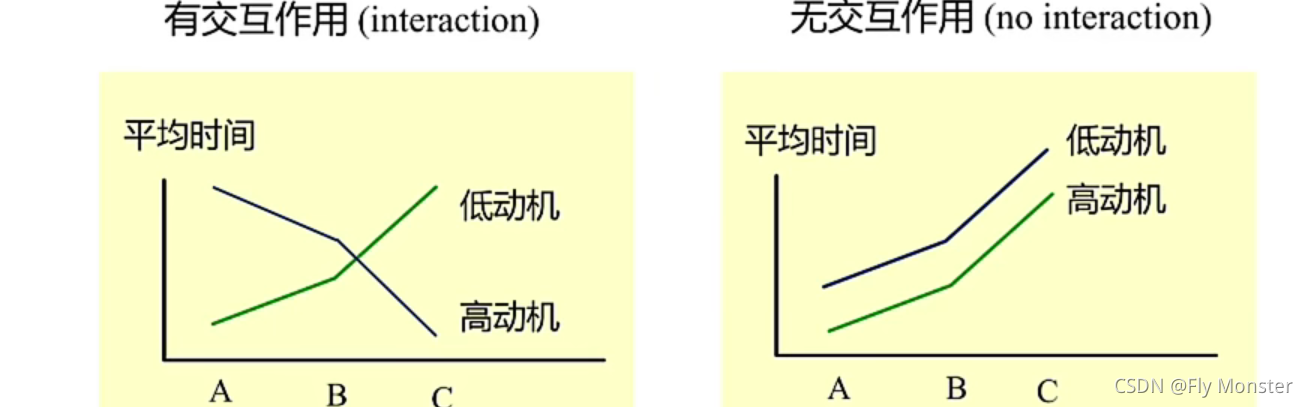
无论是什么活动,影响产品质量和产品的因素都有多种,如影响农作物产量的因素有品种、天气、施肥量、肥料的种类等等。如果我们想要了解这些因素中哪些因素对产量有显著性影响,或各个因素之间的交互作用,以及对结果有显著影响的因素的最佳水平等,就必须先进行实验,再进行分析,最后做出判断。
概念:
方差分析:又称为变异分析,是英国统计学家R.A.Fisher于1923年提出的一种统计方法,故有时也称为F检验。可简写为ANOVA。用于多组均数之间的显著性检验。
使用要求:
各组数据服从正态分布或近似正态分布,并且各组之间方差具有齐性。
基本思想:

计算原理:
三种变异的关系为:SST = SSB + SSW,DT = DB+ DW (Excel中显示略有不同)
分析步骤:
1.建立检验假设
H0:多个样本总体均值相等;
H1:多个样本总体均值不相等或不全等。
设定检验水准为0.05(Excel中为α=0.05,下文会提到。)
2.计算检验统计量F值
3.确定P值并作出推断结果(有兴趣可以研究下,刚学我只会用)
例题
假设在温度不同,其他条件适宜且相等的情况下,对统一菌型的细菌进行培养。
现在我们想知道温度不同对于该细菌存活影响是否有区别。
算出:μ=6.17(所有数的平均值),μA=4 , μB=7.22 , μC=7.27
假设:
H0:A,B,C三组温度下细菌存活结果没有区别,即μA= μB= μC
H1:A,B,C三组温度下细菌存活结果有区别。
1.首先我们需要求SST,SSB,SSW
2.求自由度 DT,DB,DW
3.最后我们求F,F的公式为F = (SSB/DB) / (SSW/DW)
F>F(DB,BW)则说明有显著差异(笔算可对照此表得出F(DB,DW)的值)
第1步:选择分析工具。“数据”——“数据分析”——“方差分析:单因素方差分析”。如下图所示。
第2步:设置相关参数。在弹出的“方差分析:单因素方差分析”对话框中,设置“输入区域”为“$K 4 : 4: 4:V 6 ” , 点 击 “ 分 组 方 式 ” 的 “ 行 ” 单 选 按 钮 , 选 择 “ 标 志 位 于 第 一 列 ” , 设 置 “ α ” 为 “ 0.05 ” , 在 “ 输 出 选 项 ” 下 单 击 “ 输 出 区 域 ” , 设 置 区 域 为 “ 6”,点击“分组方式”的“行”单选按钮,选择“标志位于第一列”,设置“α”为“0.05”,在“输出选项”下单击“输出区域”,设置区域为“ 6”,点击“分组方式”的“行”单选按钮,选择“标志位于第一列”,设置“α”为“0.05”,在“输出选项”下单击“输出区域”,设置区域为“K$10”,确定即可。设置α=0.05,表示数据有95%的可信度。
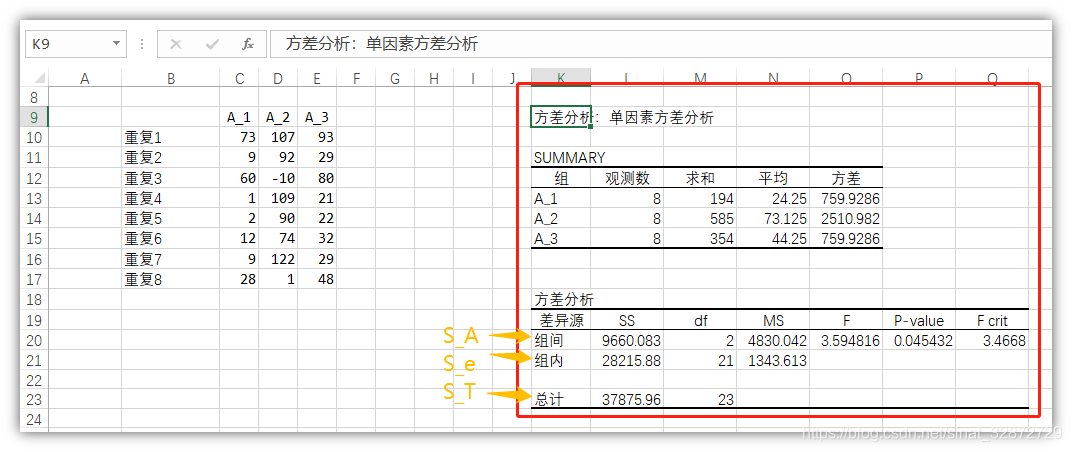
第3步:显示单因素方差分析结果。如下图所示。
4、决策分析
如上图所示,单因素方差分析的结果有两部分,第一个部分是SUMMARY,即对各个水平下的样本数据的描述统计,包括样本观测数、求和、样本平均数、样本方差。第二部分是方差分析,其中“差异源”即方差来源,SS代表平方和(分别对应SSB,SSW),df(分别对应DB,DW)代表自由度,MS指均方,F是检验统计量,P-value是观测到的显著性水平,Fcrit是检验临界值,可通过P-value的大小来判断组件的差异显著性,通常情况下,当P值<=0.01时,则表示有极显著的差异;当在0.01和0.05之间时,表示有显著差异;当该值>=0.05时,表示没有显著差异。另外,通过F值也可以判断差异显著性,当F>=Fcrit时,表示有显著差异。
在上面的案例中,P-value=0.00379<0.01,F=6.902959>Fcrit=3.354131,都说明在α=0.05的情况下,温度不同情况下对于该细菌存活有显著区别。
以上就是所有内容,仅当作个人学习中的记录,有不正之处请指出。