原标题：清华学神尹成带你实战Rust编程(1)

Rust 语言是一种高效、可靠的通用高级语言。其高效不仅限于开发效率，它的执行效率也是令人称赞的，是一种少有的兼顾开发效率和执行效率的语言。

Rust 语言由 Mozilla 开发，最早发布于 2014 年 9 月。Rust 的编译器是在 MIT License 和 Apache License 2.0 双重协议声明下的免费开源软件。截至目前( 2020 年 1 月)最新的编译器版本是 1.41.0。

Rust 官方在线工具: https://play.rust-lang.org/。

Rust 系列文章内容由 Sobin 收集整理。Rust语言的特点

高性能 - Rust 速度惊人且内存利用率极高。由于没有运行时和垃圾回收，它能够胜任对性能要求特别高的服务，可以在嵌入式设备上运行，还能轻松和其他语言集成。

可靠性 - Rust 丰富的类型系统和所有权模型保证了内存安全和线程安全，让您在编译期就能够消除各种各样的错误。

生产力 - Rust 拥有出色的文档、友好的编译器和清晰的错误提示信息， 还集成了一流的工具 —— 包管理器和构建工具， 智能地自动补全和类型检验的多编辑器支持， 以及自动格式化代码等等。Rust的应用

Rust 语言可以用于开发：

传统命令行程序 - Rust 编译器可以直接生成目标可执行程序，不需要任何解释程序。

Web 应用 - Rust 可以被编译成 WebAssembly，WebAssembly 是一种 JavaScript 的高效替代品。

网络服务器 - Rust 用极低的资源消耗做到安全高效，且具备很强的大规模并发处理能力，十分适合开发普通或极端的服务器程序。

嵌入式设备 - Rust 同时具有JavaScript 一般的高效开发语法和 C 语言的执行效率，支持底层平台的开发。谁适合阅读本教程？

本教程对于初级的编程知识将默认读者已经掌握，所以如果你阅读本教程，你需要对初级的编程知识有一定的了解(最好已经初识 C/C++ 或 JavaScript 编程语言)。第一个 Rust 程序

Rust 语言代码文件后缀名为 .rs, 如 runoob.rs。实例

fn main() { println!("Hello World!");} 参考链接

Rust 官方网站：https://www.rust-lang.org/zh-CN

Rust 官方文档：https://doc.rust-lang.org/

Rust Play：https://play.rust-lang.org/

Visual Studio Code：https://code.visualstudio.com/

Rust 环境搭建

Rust 支持很多的集成开发环境(IDE)或开发专用的文本编辑器。

官方网站公布支持的工具如下(https://www.rust-lang.org/zh-CN/tools)：

本教程将使用 Visual Studio Code 作为我们的开发环境(Eclipse 有专用于 Rust 开发的版本，对于初学者也是不错的选择)。

注意：IntelliJ IDEA 安装插件之后难以调试，所以推荐习惯使用 IDEA 的开发者使用 CLion，但 CLion 不是免费的。搭建 Visual Studio Code 开发环境

首先，需要安装最新版的 Rust 编译工具和 Visual Studio Code。

Rust 编译工具：https://www.rust-lang.org/zh-CN/tools/install

Visual Studio Code：https://code.visualstudio.com/Download

Rust 的编译工具依赖 C 语言的编译工具，这意味着你的电脑上至少已经存在一个 C 语言的编译环境。如果你使用的是 Linux 系统，往往已经具备了 GCC 或 clang。如果你使用的是 macOS，需要安装 Xcode。如果你是用的是 Windows 操作系统，你需要安装 Visual Studio 2013 或以上的环境(需要 C/C++ 支持)以使用 MSVC 或安装 MinGW + GCC 编译环境(Cygwin 还没有测试)。安装 Rust 编译工具

Rust 编译工具推荐使用刚才从上方链接中下载的 Rustup 安装。下载好的 Rustup 在 Windows 上是一个可执行程序 rustup-init.exe。(在其他平台上应该是 rustup-init.sh )。

现在执行 rustup-init 文件：

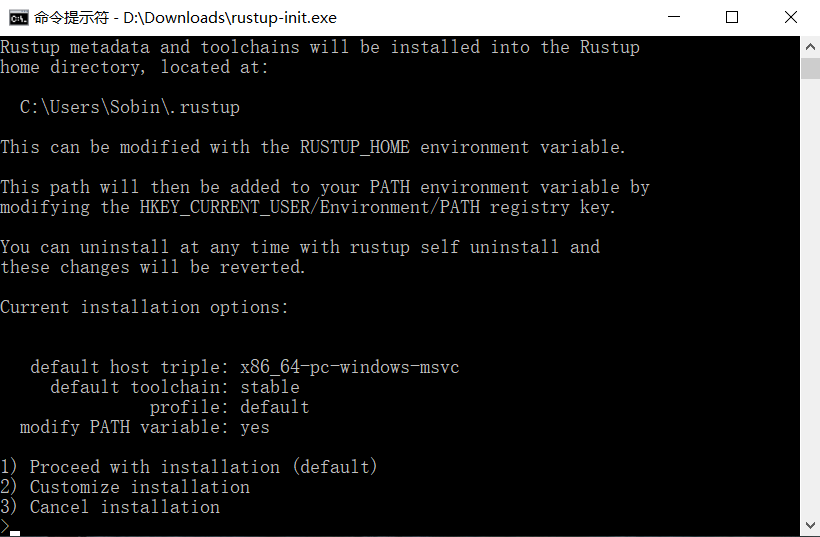
上图显示的是一个命令行安装向导。

如果你已经安装 MSVC (推荐)，那么安装过程会非常的简单，输入 1 并回车，直接进入第二步。

如果你安装的是 MinGW，那么你需要输入 2 (自定义安装)，然后系统会询问你 Default host triple? ，请将上图中 default host triple 的 "msvc" 改为 "gnu" 再输入安装程序：

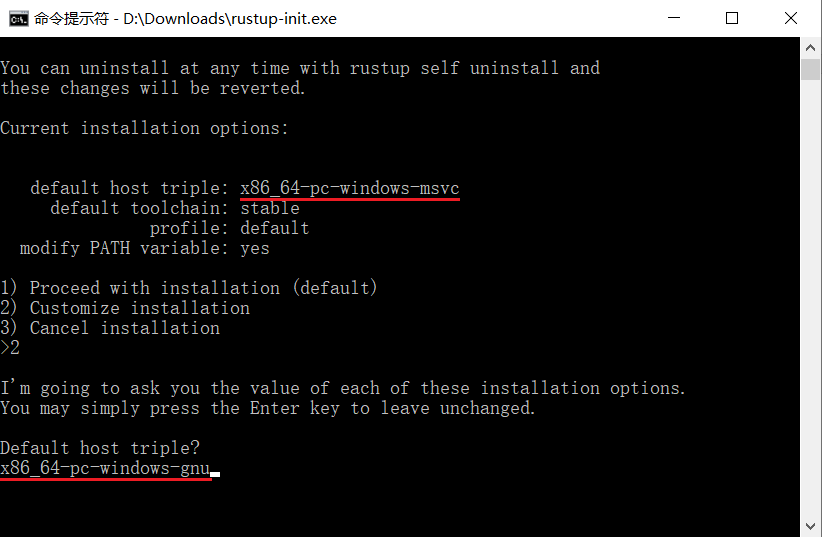
其它属性都默认。

设置完所有选项，会回到安装向导界面(第一张图)，这是我们输入 1 并回车即可。

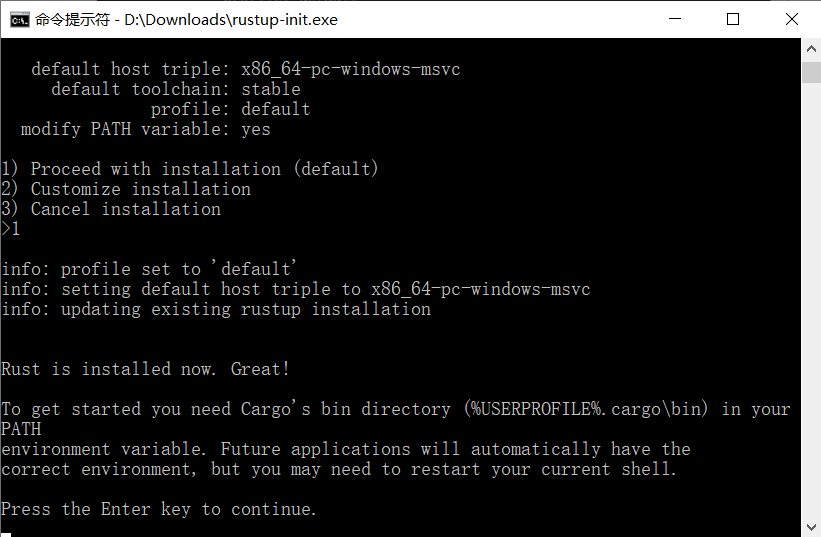
进行到这一步就完成了 Rust 的安装，可以通过以下命令测试：rustc -V # 注意的大写的 V

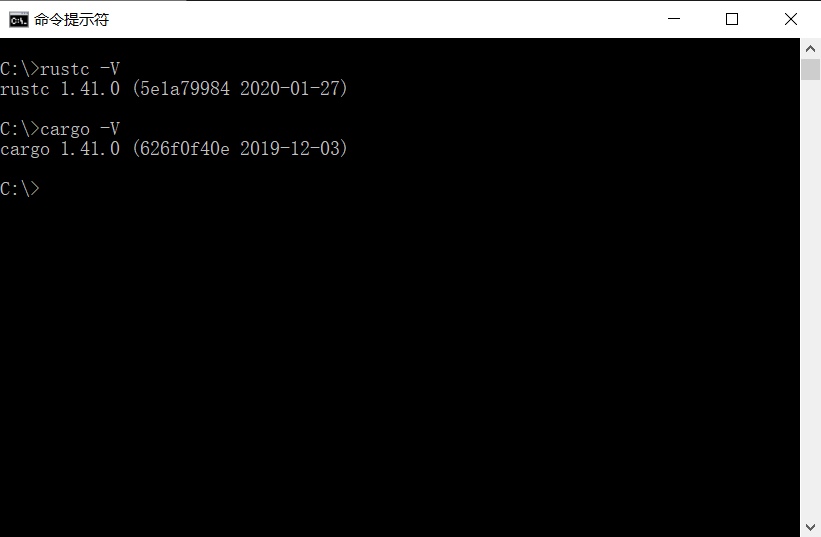
如果以上两个命令能够输出你安装的版本号，就是安装成功了。搭建 Visual Studio Code 开发环境

下载完 Visual Studio Code 安装包之后启动安装向导安装(此步骤不在此赘述)。

安装完 Visual Studio Code (下文简称 VSCode)之后运行 VSCode。

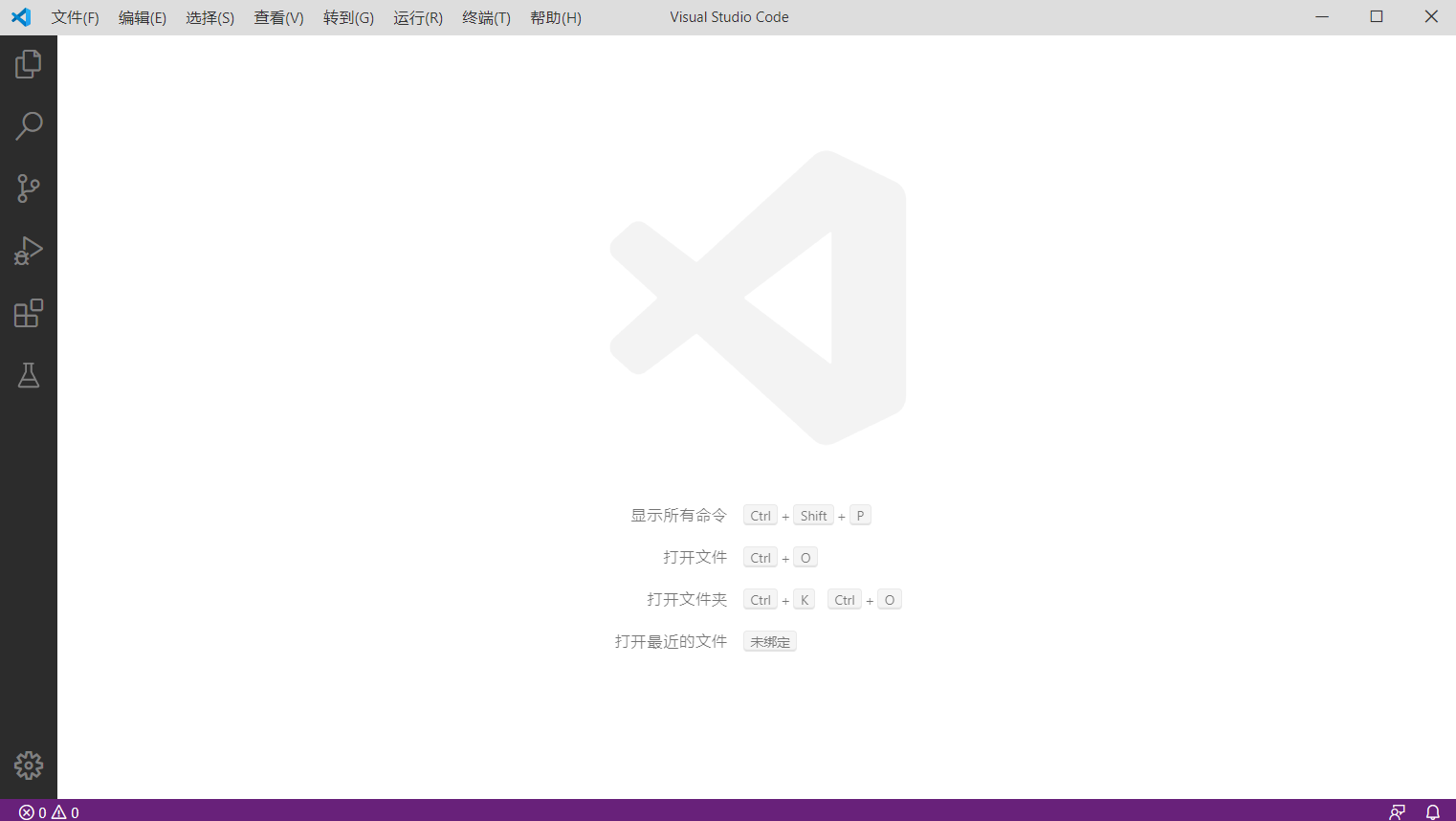
在左边栏里找到 "Extensions"，并查找 "Chinese"，安装简体中文扩展，使界面变成中文。(如果你愿意用英文界面或计算机不支持中文字符，此步骤可以跳过)。

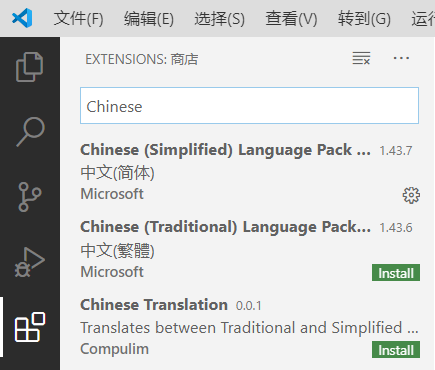
用同样的方法再安装 rls 和 Native Debug 两个扩展。

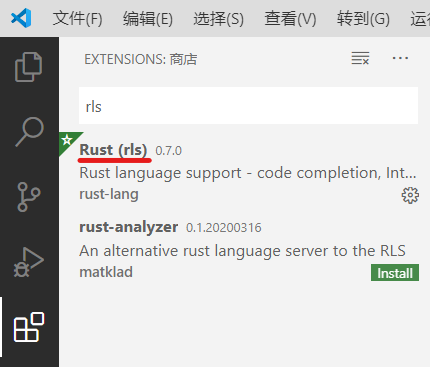
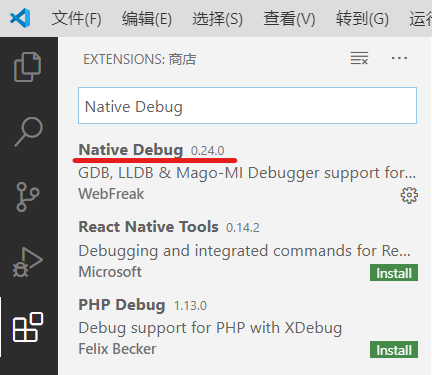
重新启动 VSCode，Rust 的开发环境就搭建好了。

现在新建一个文件夹，如 runoob-greeting。

在 VSCode 中打开新建的文件夹：

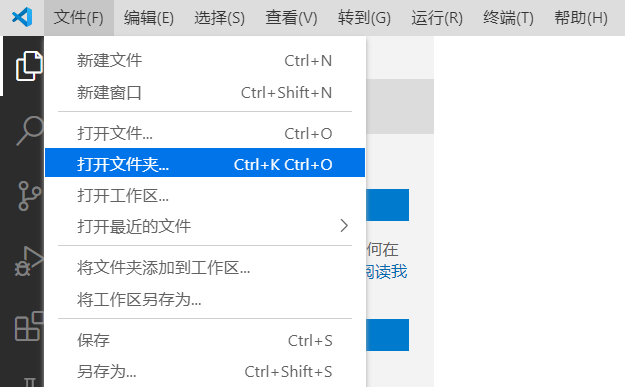
打开文件夹之后选择菜单栏中的"终端"-"新建终端"，会打开一个新的终端：

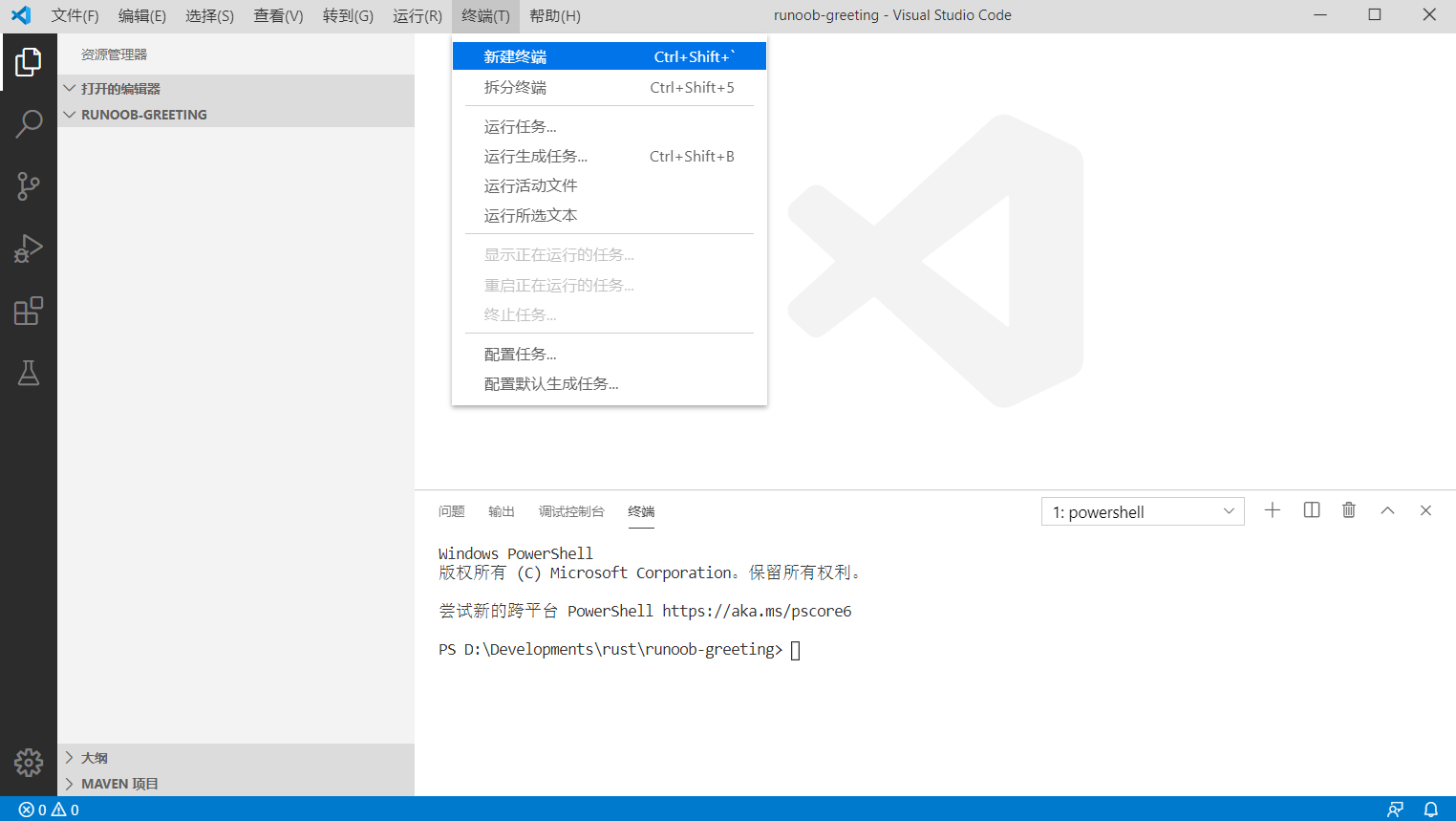
在终端中输入命令：cargo new greeting

当前文件下下会构建一个名叫 greeting 的 Rust 工程目录。

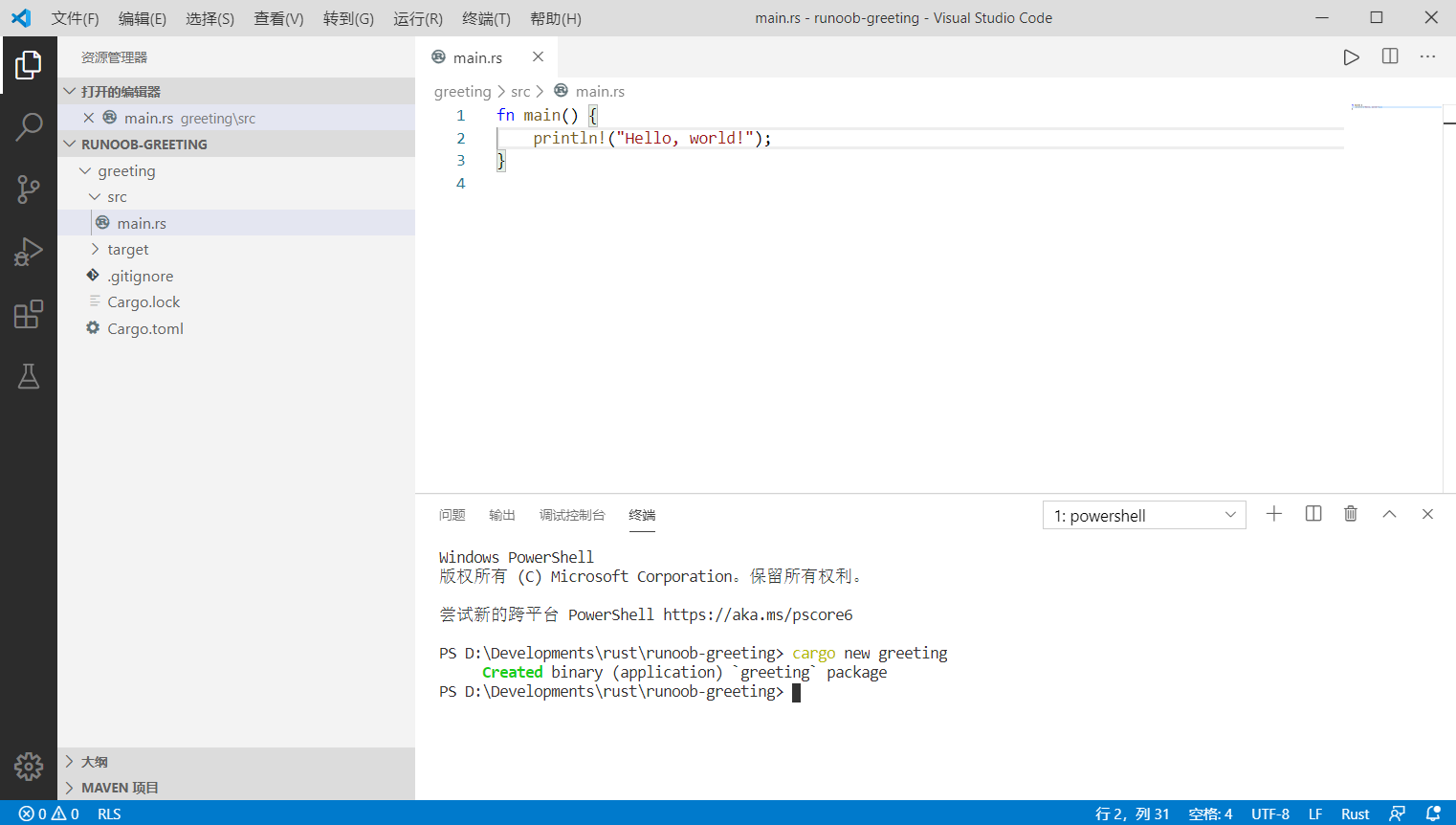
现在在终端里输入以下三个命令：cd ./greeting cargo build cargo run

系统在创建工程时会生成一个 Hello, world 源程序 main.rs，这时会被编译并运行：

至此，你成功的构建了一个 Rust 命令行程序！返回搜狐，查看更多

责任编辑：