伯努利分布(Bernoulli distribution)

article/2025/9/17 15:49:46

伯努利分布是一种离散分布,有两种可能的结果。1表示成功，出现的概率为p(其中0<p<1)。0表示失败，出现的概率为q=1-p。这种分布在人工智能里很有用，比如你问机器今天某飞机是否起飞了，它的回复就是Yes或No，非常明确，这个分布在分类算法里使用比较多，因此在这里先学习一下。

概率分布有两种类型：离散（discrete）概率分布和连续（continuous）概率分布。
离散概率分布也称为概率质量函数（probability mass function）。离散概率分布的例子有伯努利分布（Bernoulli distribution）、二项分布（binomial distribution）、泊松分布（Poisson distribution）和几何分布（geometric distribution）等。
连续概率分布也称为概率密度函数（probability density function），它们是具有连续取值（例如一条实线上的值）的函数。正态分布（normal distribution）、指数分布（exponential distribution）和β分布（beta distribution）等都属于连续概率分布。

二项分布的例子：抛掷10次硬币，恰好两次正面朝上的概率是多少？
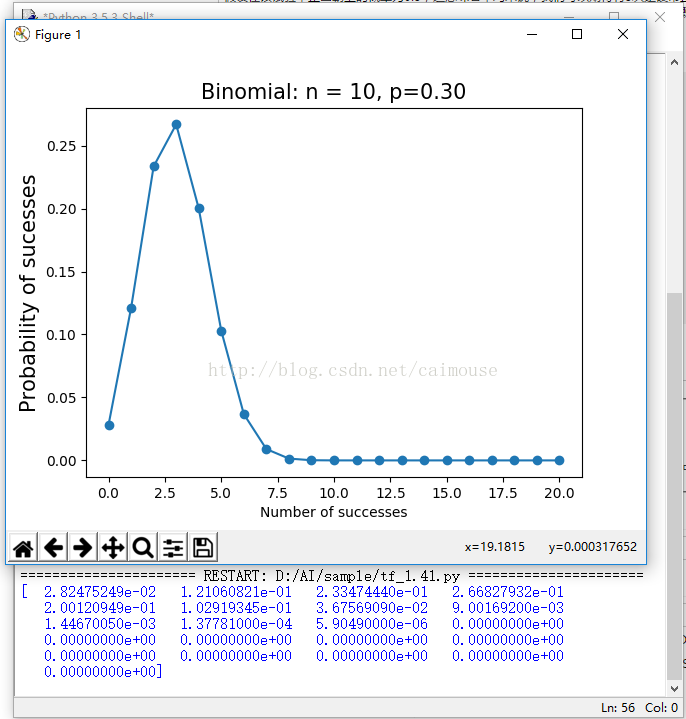
假设在该试验中正面朝上的概率为0.3，这意味着平均来说，我们可以期待有3次是硬币正面朝上的。我定义掷硬币的所有可能结果为k = np.arange(0,11)：你可能观测到0次正面朝上、1次正面朝上，一直到10次正面朝上。我使用stats.binom.pmf计算每次观测的概率质量函数。它返回一个含有11个元素的列表（list），这些元素表示与每个观测相关联的概率值。

对于这样的问题，可以使用python来解决，这样理解起来更容易得多了，代码如下：

#python 3.5.3  蔡军生    
#http://edu.csdn.net/course/detail/2592    
#  
from scipy.stats import binom
import matplotlib.pyplot as plt
import numpy as npn = 10
p = 0.3
k = np.arange(0, 21)
binomial = binom.pmf(k, n, p)
print(binomial)plt.plot(k, binomial, 'o-')
plt.title('Binomial: n = %i, p=%0.2f' % (n, p),fontsize = 15)
plt.xlabel('Number of successes')
plt.ylabel('Probability of sucesses', fontsize = 15)
plt.show()

运行这个程序之后，就可以输出这样的结果了，是否一目了然的感觉？