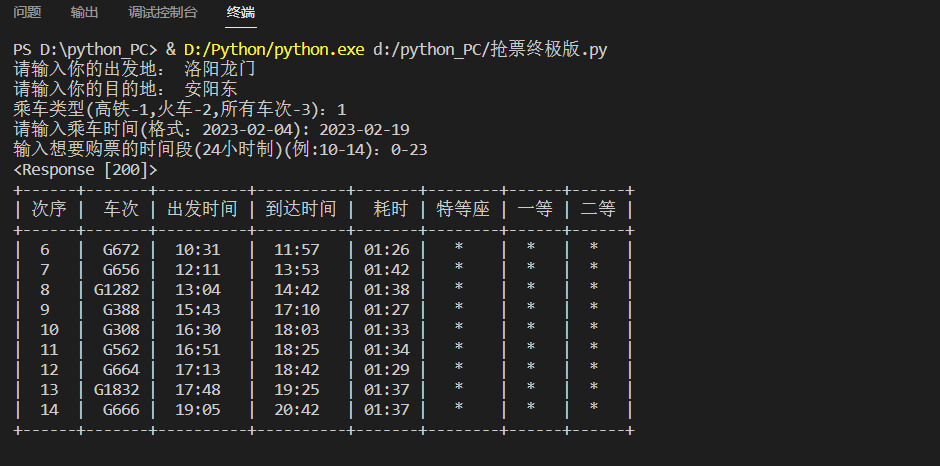
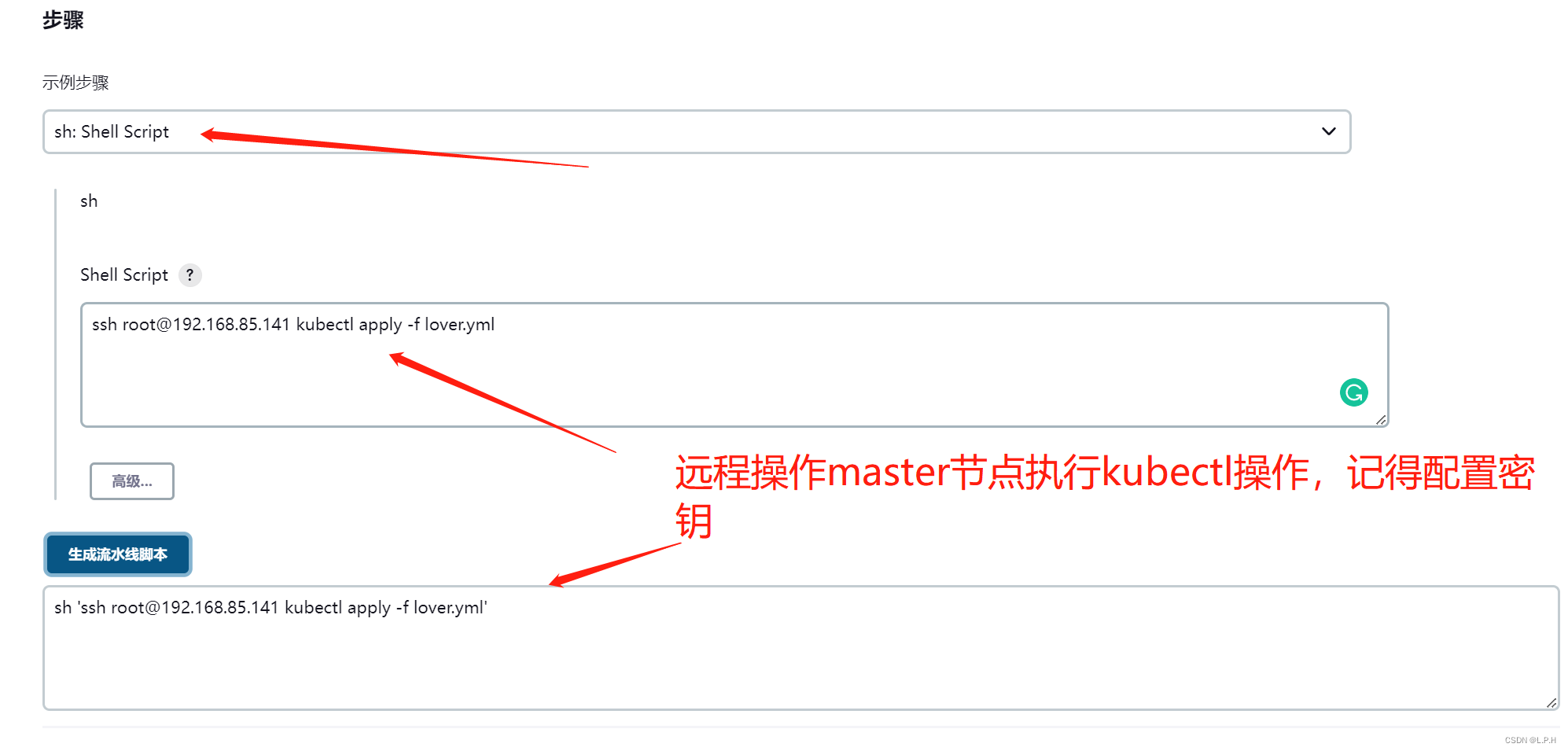
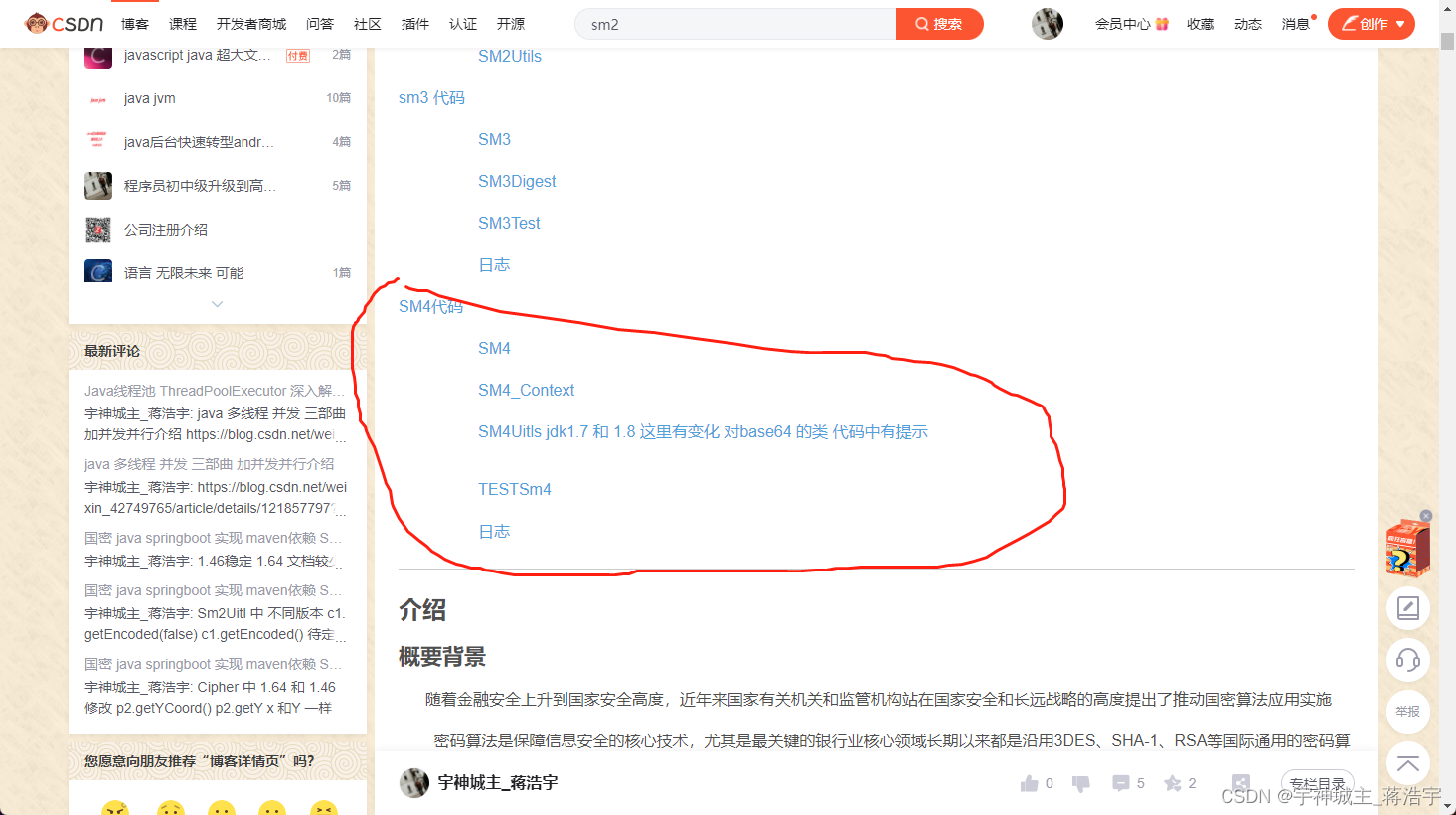
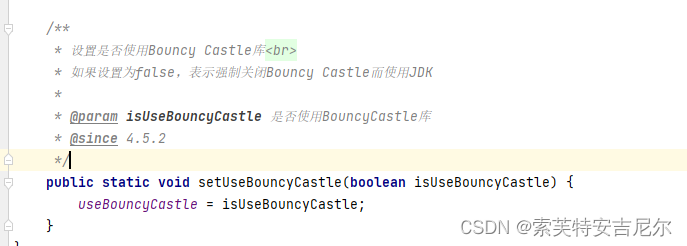
师兄给我说,做机器学习的方法有两种:一种是修改公式的那种,另外一种是类比。我觉得我适合的应该就是类比的这种,公式太难了。。
伯努利分布
记住这种分布的话,就开始想抛硬币,只抛一次硬币。正面朝上的概率是p,反面朝上的概率是q。k=1
二项分布
这种分布也是抛硬币,只不过是抛多次硬币。B(n,p) 也就是这里面总共有两个参数,一个是n,另外一个是p。n是总共抛硬币的总数,p是正面朝上的概率,那个反面朝上的概率就是1-p。
对于抛硬币,我们可以想象两种不同的过程。
第一种过程是我们最终的目的是要估计总体的参数,也就是p,也就是给我很多样本,让我估计这两个值。就相当于是让我抛硬币,抛很多次,记录每一次是正面朝上还是反面朝上,那么我抛的次数越多,最终得到的p的值就准确。
第二种就是高中数学常考的题目,就我们根据常识已经知道抛一次硬币的话,正面朝上的概率是1/2,也就是我们已经知道总体的参数了,然后给我说,我抛8次硬币,2正面朝上的概率是多少。这时候我们可以用概率质量函数来求P(x)=C2 8 (1/2) 2(1-1/2)6 。在这个过程中,我们求的是概率。
上面这两个过程分别是求似然和求概率的过程。第一个过程可以表示成为L(p|A),第二个过程可以表示为P(A|p),这里面的p就是那个总体参数,A就是抛1次,2次,3次……这样的抛硬币的过程。
并且L(p|A)=P(A|p)。
举例
https://www-pnas-org.eproxy.lib.hku.hk/doi/full/10.1073/pnas.1419161111#eq3
https://www.sciencedirect.com/science/article/pii/S0002929720302354
这篇文章中使用了二项分布

接下来开启类比模式:
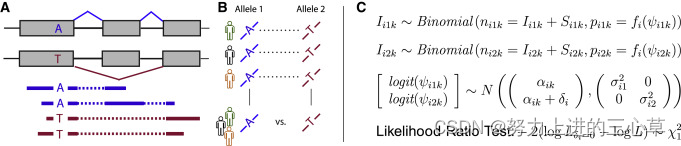
在RNA-seq中,经过测序,我们得到n个reads, 根据上面这两张图,我们把reads分成两类,一类是比对到 exon inclusion isoform 上的reads,另外一类是比对到exon skipping isoform上的reads 。
上面的过程就类比成了抛硬币,总共抛了n次硬币,每一次有两种可能性,比对到exon inclusion isoform上 (正面朝上),比对到exon skipping isoform (反面朝上)。
在科研里面我们都是要求参数,在这里面也就是求p ,也就是抛硬币里面的1/2。因为我们有很多个样本,我们是想根据这些所有的样本得到一个总体的参数。根据这些给出的样本,我们可以计算出来L(p|A),然后再根据最大似然,求出参数p。
接下来我们就看看文章中方法部分的公式:

在这里面最终要估计的参数是psi, I是能够比对到exon inclusion isoform上的count数,S是能够比对到exon exclusion isoform上的count数。p是来自exon inclusion isoform的reads的比例。
把上面的话用硬币的方式来表示应该就是 : 在给定p的情况下,总共抛了n次硬币,正面朝上的概率是多少。然后这个p指的就是正面朝上的概率,它对应的应该就是这个reads 比对到exon inclusion isoform的比例。 n是总共的reads数,通过样本,我们可以得到p,但是我们的目的是求psi,也就是isoform 1 /(isoform1 +isoform2) .。 p和psi 之间的关系可以通过f(PSI) 这个函数表示出来。在其中加入两种isoform 的effect length。
多项分布
多项分布可以看成是掷色子,可能出现的结果有多个。每一次掷色子是离散随机变量。
举个例子
https://genomebiology.biomedcentral.com/articles/10.1186/s13059-021-02461-5#Sec8
理解了二项分布的过程,多项分布就很容易了。
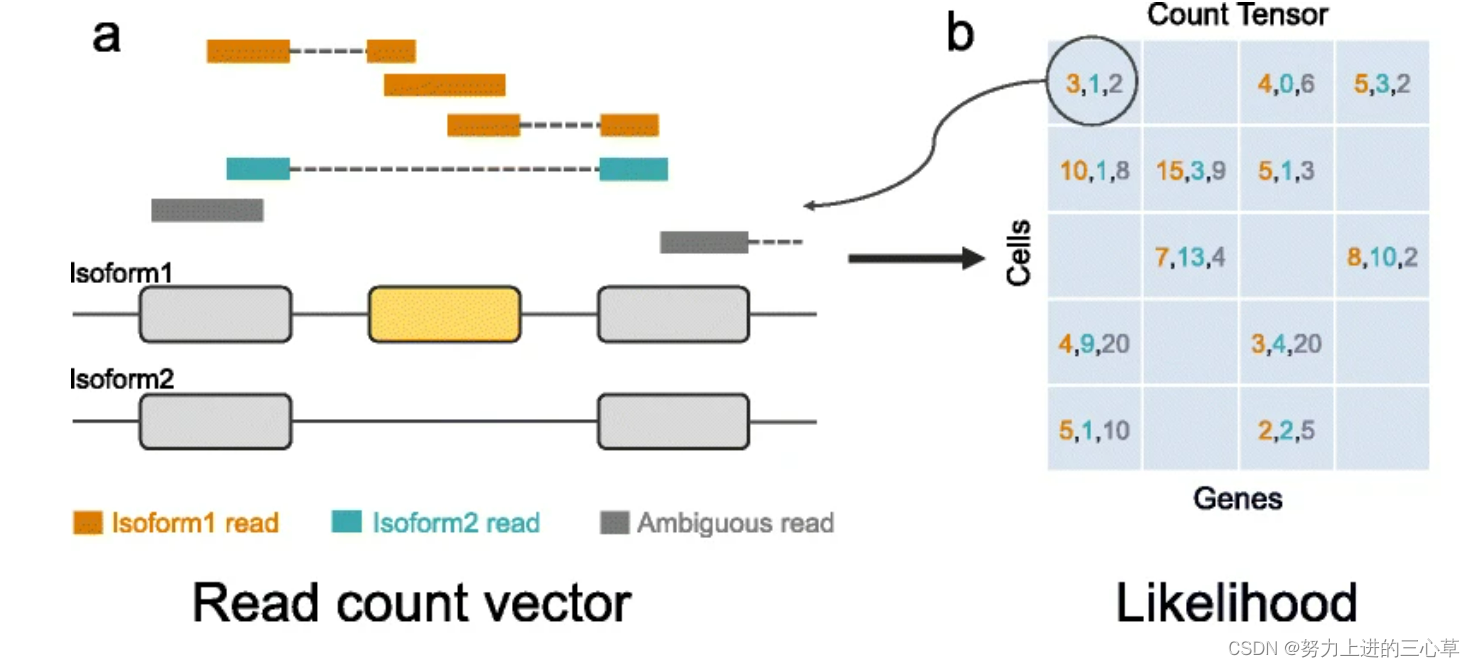
在这里把reads比对到isoform的过程分成了三种类型,第一种就是直接比对到isoform1上的,第二种是比对到isoform2上的,第三种是ambiguous reads 。

在这里我们可以根据多个样本计算出每一个细胞,每一个基因的ψ值,因为每一个reads属于哪一个isoform服从多项分布。ρ是每一种类型的reads占总数的reads的比例,然后ρ和psi的关系用公式1来表示。
二项混合模型
混合模型是基于单个模型,有多个components 。
举个例子
https://www.nature.com/articles/s41467-022-28845-0#Sec2
未完待续





![[cryptoverse ctf 2022] cvctf](https://img-blog.csdnimg.cn/a6805ee635a243a7b4286b0d4f411df2.jpeg)