基于python/scipy学习概率统计(2)：伯努利分布(Bernoulli Distribution)

article/2025/9/18 4:24:17

1. 概念

2. 概率分布

2.1 概率质量函数

2.2 概率分布函数

2.3 生存函数，风险函数

2.4 百分点函数

3. 常用统计特征

3.1 均值，Mean

3.2 中位数，Median

3.3 众数，Mode

3.4 方差，Variance

3.5 偏度，Skewness

3.6 峰度，Kurtosis

4. 代码示例

1. 概念

设试验E只有两种可能的结果，这种试验称为伯努利试验。伯努利试验的结果为一个随机变量，它遵循伯努利分布。

伯努利分布也称为(0-1)分布，遵循伯努利分布的随机变量只有两种取值，分别用0和1表示（分别对应试验的两种结果）。典型的例子是扔硬币实验结果。将扔硬币的实验结果（正面向上或向下）看作是一个随机变量X，则X遵循伯努利分布，这是一种离散分布。记为：

$X \sim Bern(p)$

$X\sim B(p)$

其中通常p表示X取值为1的概率。

2. 概率分布

2.1 概率质量函数

PMF: Probability Mass Function

有些书也写作分布律（如浙大版<<概率论与数理统计>>），与连续随机变量的PDF（Probability Density Function: 概率密度函数）相对应）。

伯努利分布的概率质量函数为：

$P(X=1|p) = p \\ P(X=0|p) = 1-p$

当然，为了和条件概率区分开来，也有将写成的写法。一般情况下根据上下文也可以做出区分。

也可以进一步简记（未必简单，但是对于要做数学推导处理等就比较方便）为：

其中I(x)是所谓的Indicator函数。因此，以上式表示仅在x=0或x=1时成立，其它情况下则为0.

2.2 概率分布函数

伯努利分布的概率分布函数（CDF: Cumulative Distribution Function，累积分布函数。不管对于离散随机变量还是连续随机变量，CDF总是一个连续函数。只不过对于离散随机变量而言，CDF是一个分段函数：piecewise function）如下所示：

2.3 生存函数，风险函数

生存函数是概率分布函数的互补函数，定义为： $S(x)=F(1-x)$ 。伯努利分布的生存函数为：

与生存函数相关联风险函数定义为：

注意，风险函数仅在S(x)的非零区间（In other words, only valid on S support）有定义。伯努利分布的风险函数为：

伯努利分布的累计风险函数为:

(???待确认)

2.4 百分点函数

PPF: Percent Point Function. 也称百分位数(percentile)?

百分点函数PPF是CDF的反函数，它回答了“为了得到一定的累积分布概率，CDF相应的输入值是什么”的问题。伯努利分布的百分点函数为：

3. 常用统计特征

3.1 均值，Mean

$\mu = E(X) = p$

3.2 中位数，Median

3.3 众数，Mode

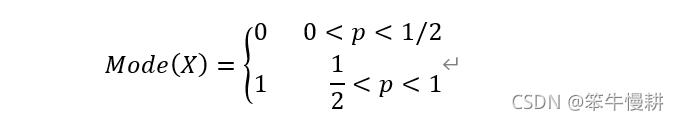
3.4 方差，Variance

$V(X)=\sigma^2 = p(1-p)$

3.5 偏度，Skewness

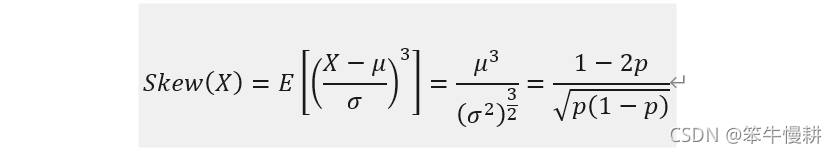
3.6 峰度，Kurtosis

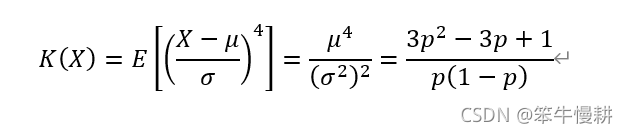
4. 代码示例

首先，导入必要的库。

import random
import numpy as np
from scipy.stats import bernoulli
%matplotlib inline
from matplotlib import pyplot as plt

看看p=0.4条件下的PMF函数：

fig, ax = plt.subplots(1, 1)
p  = 0.4
x = np.arange(-1,3)
ax.plot(x, bernoulli.pmf(x, p), 'bo', ms=8, label='bernoulli pmf')
ax.vlines(x, 0, bernoulli.pmf(x, p), colors='b', lw=5, alpha=0.5)#rv = bernoulli(p)
#ax.vlines(x, 0, rv.pmf(x), colors='k', linestyles='-', lw=1, label='frozen pmf')
ax.legend(loc='best', frameon=False)
ax.grid()
plt.show()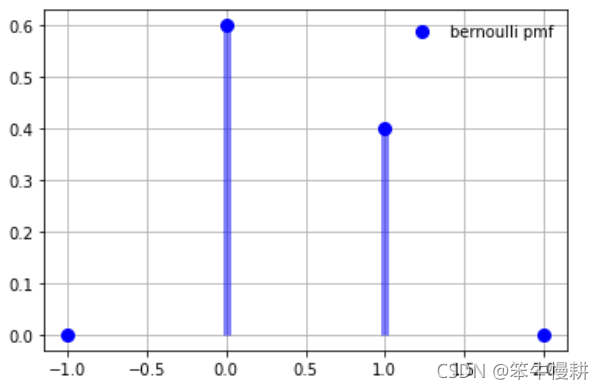

x=0时概率等于0.6, x=1时等于0.4，符合预期。

看看CDF与PPF的关系（它们是互逆的关系）：

cdf_prob = bernoulli.cdf(x, p)
print('cdf_prob[{0}] = {1}'.format(x,cdf_prob))
print('ppf[{0}] = {1}'.format(cdf_prob,bernoulli.ppf(cdf_prob, p)))

Output:

        cdf_prob[[-1  0  1  2]] = [0.  0.6 1.  1. ]ppf[[0.  0.6 1.  1. ]] = [-1.  0.  1.  1.]

注意存在在不满足可逆条件的区间。cdf(2) = 1, 而ppf(1) = 1。这是可以理解的。因为对于在x>=1的区间，cdf的定义域到值域不是一一映射，因此不可逆。所以ppf(cdf(x))不一定等于x。

4种常用的统计特征:

p=0.5
mean, var, skew, kurt = bernoulli.stats(p, moments='mvsk')
print('Bernoulli distribution with p ={}'.format(p))
print('mean = {0}, var = {1}, skew = {2}, kurt = {3}'.format(mean, var, skew, kurt))p=0.4
mean, var, skew, kurt = bernoulli.stats(p, moments='mvsk')
print('Bernoulli distribution with p ={}'.format(p))
print('mean = {0}, var = {1}, skew = {2}, kurt = {3}'.format(mean, var, skew, kurt))

当p=0.5时，说明0和1是等概率的，因此是一个对称的分布，因此3阶中心矩(对应Skewness)变为0。p!=0.5时，分布变为非对称的了，skewness变为非0就显示了分布非对称性。

来看看实际采样实验，即基于scipy.stats提供的函数进行随机数采样，然后看看它的统计特征是否符合预期。

r = bernoulli.rvs(p, size=10000)
_ = plt.hist(r, bins='auto', density=True)  # arguments are passed to np.histogram
plt.title("Histogram with 'auto' bins")
plt.grid()
plt.show()print('sample means of r = {0}'.format(np.mean(r)))
print('sample variance of r = {0}'.format(np.var(r)))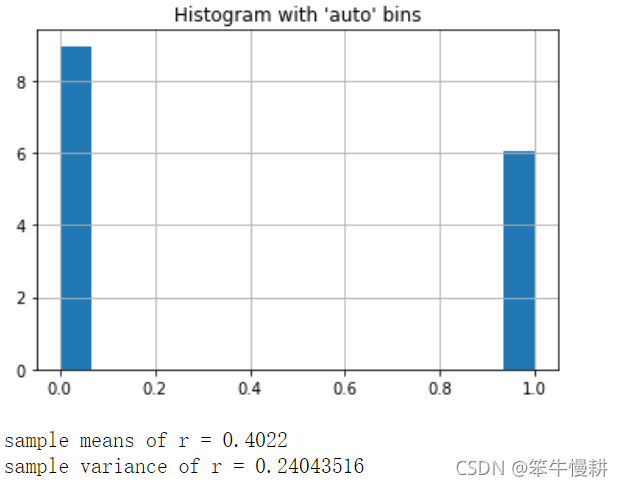

mean和variance是符合预期的。

但是直方图上（虽然已经选择了是density=True），所显示的两个离散点的值的和并不为1。这个是numpy的histogram()函数（plt.hist()是调用numpy的histogram()）的行为所致，查阅numpy.histogram()的手册有如下说明：

histogram() parameter: densitybool, optional If False, the result will contain the number of samples in each bin. If True, the result is the value of the probability density function at the bin, normalized such that the integral over the range is 1. Note that the sum of the histogram values will not be equal to 1 unless bins of unity width are chosen; it is not a probability mass function.

但是这个毕竟不甚方便，需要琢磨一下如何让直方图能够进行归一化计算和显示。

上一篇：面向机器学习的概率统计：均匀分布(Uniform Distribution)https://blog.csdn.net/chenxy_bwave/article/details/120725136https://blog.csdn.net/chenxy_bwave/article/details/120725136