首先说伯努利试验

伯努利分布
伯努利试验说的是下面一种事件情况:在生活中,有一些事件的发生只有两种可能,发生或者不发生(或者叫成功或者失败),这些事件都可以被称为伯努利试验。
伯努利试验的概率分布称为伯努利分布(两点分布、0-1分布),如果记成功概率为p,则失败概率为q=1-p,则:
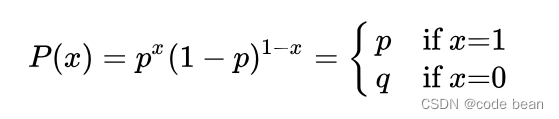
二项分布
假如某个试验是伯努利试验。进行n次这样的试验,成功了x次,则失败了n-x。二项分布认为:发生这种情况的概率可以用下面公式来计算:
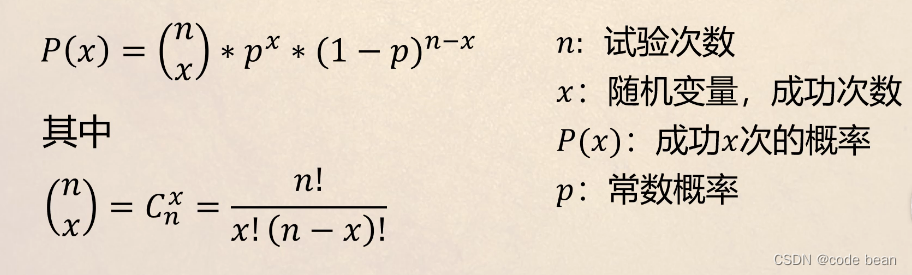
二项分布的概率质量函数可以简写为X~B(n,p)。
实际上,当n = 1时,二项分布就是 伯努利分布。这就是二项分布和伯努利分布的关系。

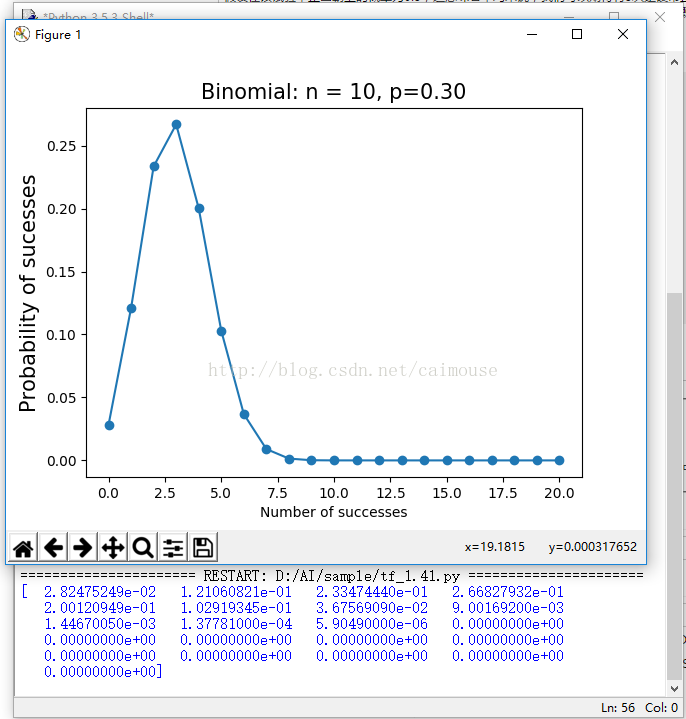
所以这里我们可以看到,二项分布是一个离散的分布的直方图。X轴为成功次数,Y轴对应的是成功n次数概率值。
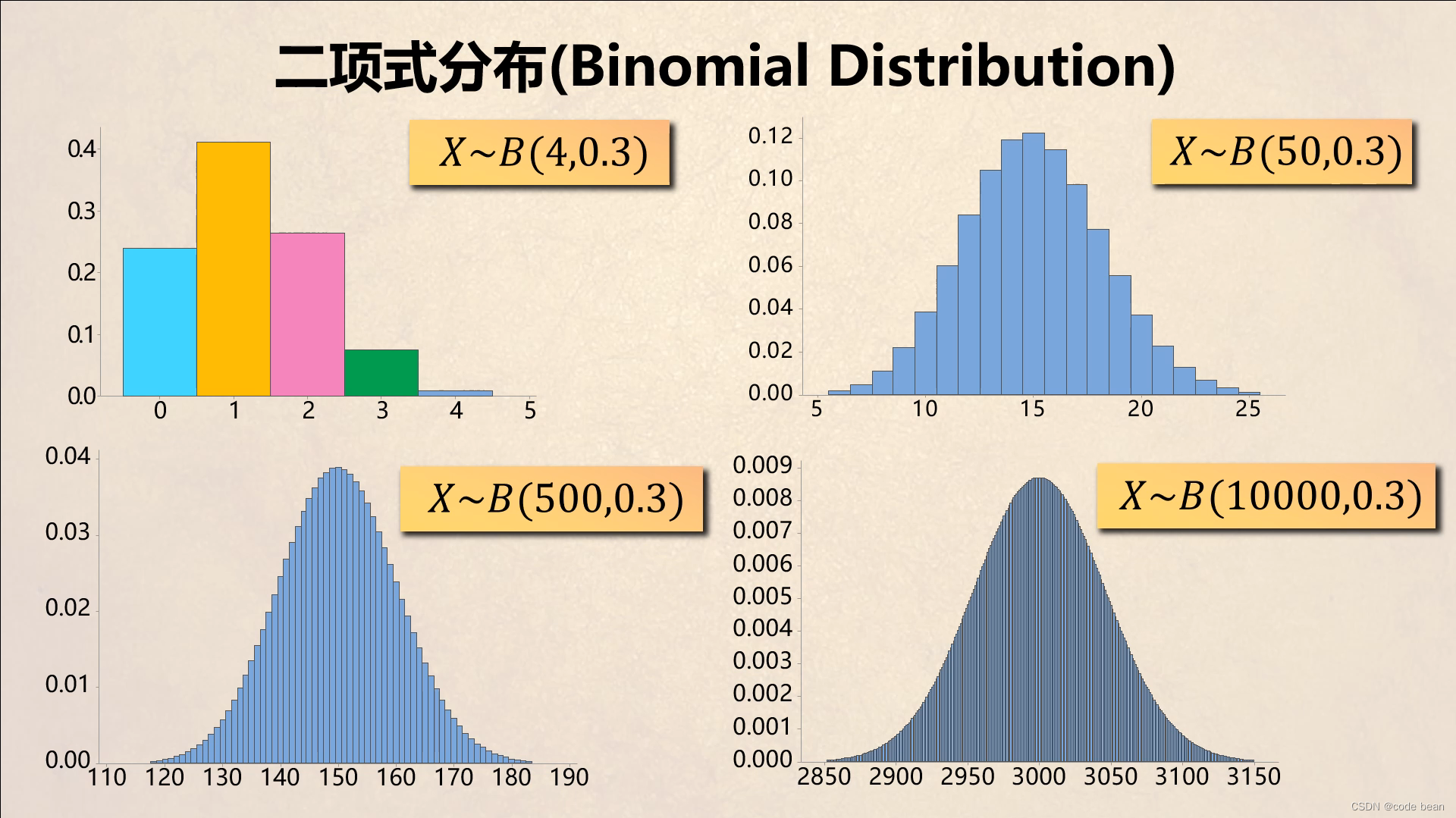
随着实验次数的递增,我们将得到一个类似正态分布的直方图。
一个有趣的例子(关于二项分布)
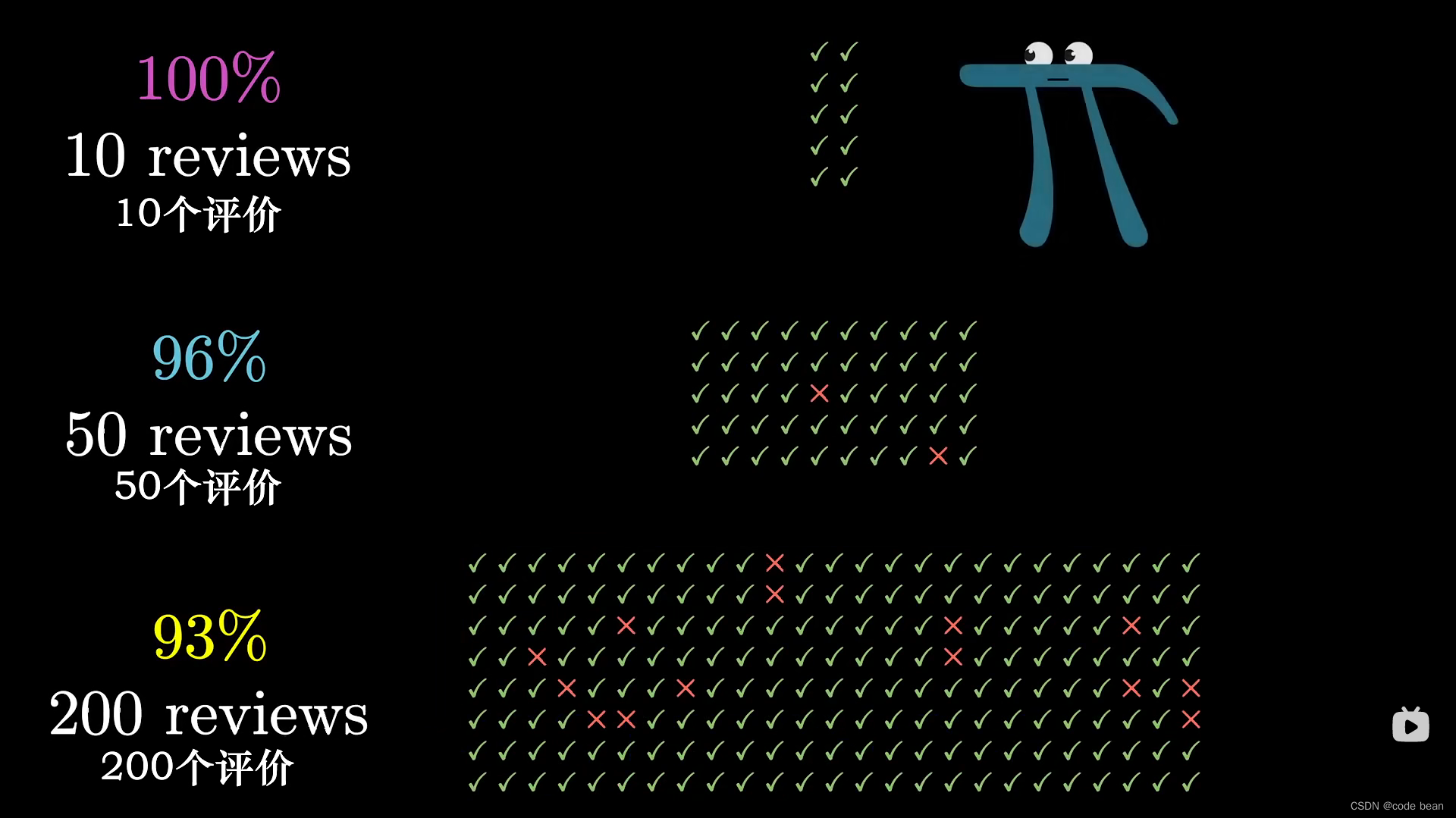
他将的是如果你去京东购物,你想买一款自行车,然后淘了三家店铺,第一家店铺共条10条评论,都是好评。第二家,50条评论,96%的好评,第三家,200条评论96%的好评。那我应该选哪家店进行购买。这里我假设一个前提,假设自行车质量OK的概率是x(质量NG的概率是1-x),当买家买到OK的自行车就会给出好评,否则差评。
那么看第一家,10条评论,都是好评。那么能说明第一家的自行车良品率是100%吗?不一定吧。我们假设第一家自行车的良品率是0.95。那么每次抽取10自行车都为OK的概率其实还挺高的(相当于10个顾客买到都OK自行车的概率)。
下图表示,如果自行车的良品率是0.95,每次抽10辆,分别抽取7,8,9,10辆是OK的概率。
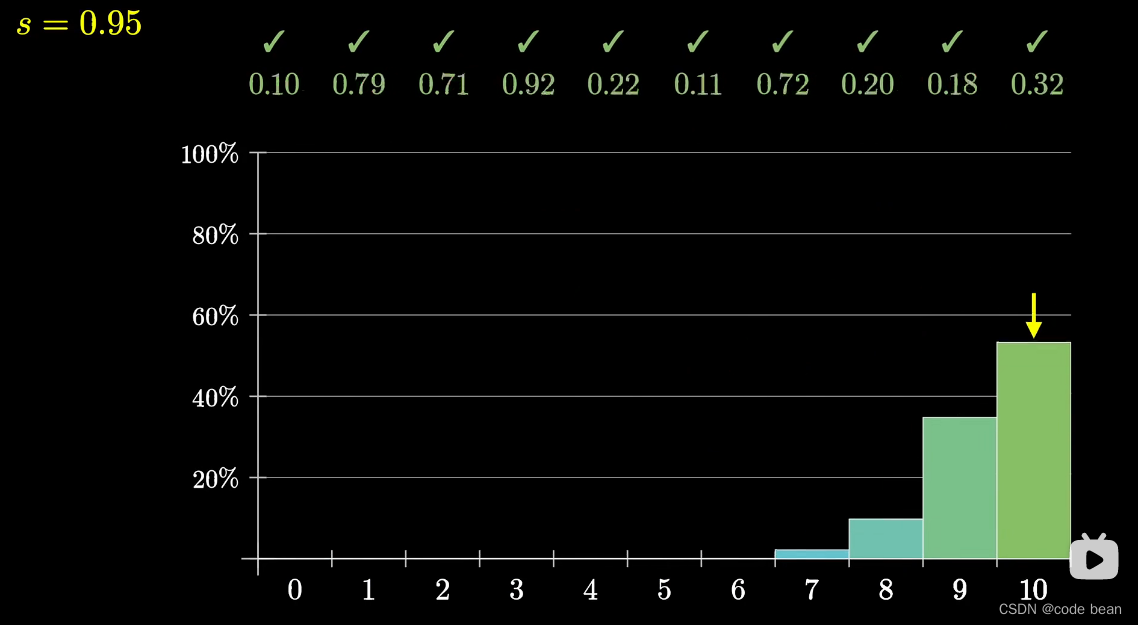
也就是说,虽然10条评论,都是好评。但是自行车的OK率也是不确定的。但是根据这个二项分布,你说这家店的良品率在0.95左右,感觉还是可以的。总的来说样本太少,可能的情况很多。
也就是说,如果前确定了良品率,可以看到好评率的概率
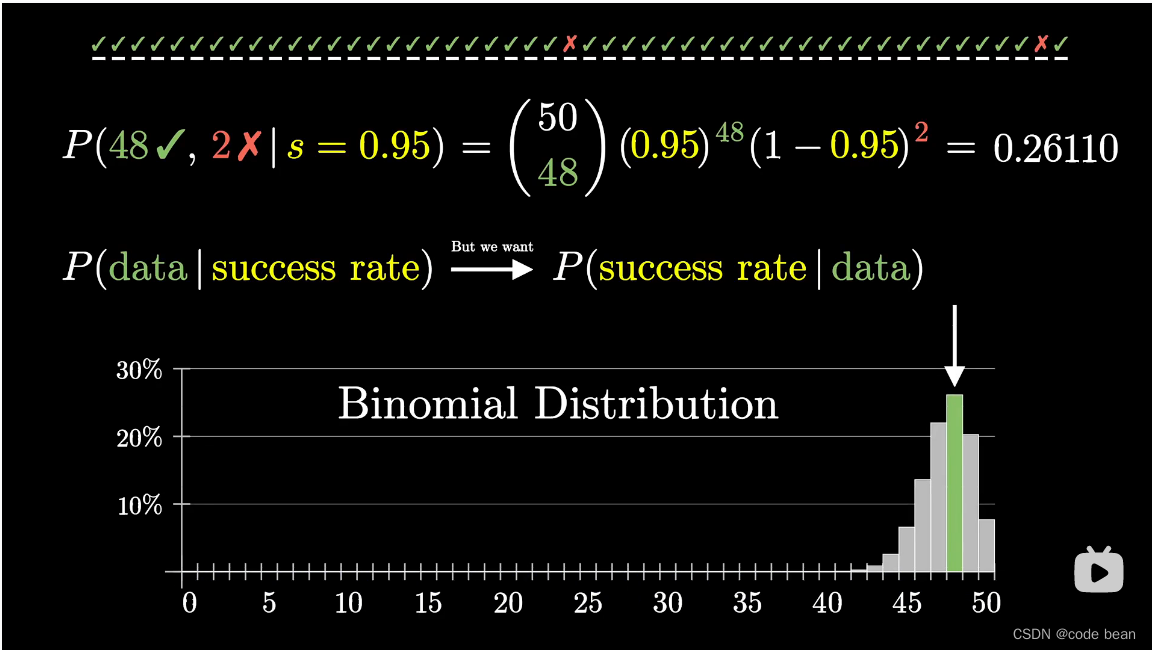 比如,如果良品率是0.95,那么如果有50条评论,其中有48条是好评的概率是0.26110(出现47条或49条好评也在0.2以上)
比如,如果良品率是0.95,那么如果有50条评论,其中有48条是好评的概率是0.26110(出现47条或49条好评也在0.2以上)
那么反过来,如果我们已知了一个好评的二项分布,能不能推出最有可能的良品率?那么其实分布和良品率s有对应的关系。
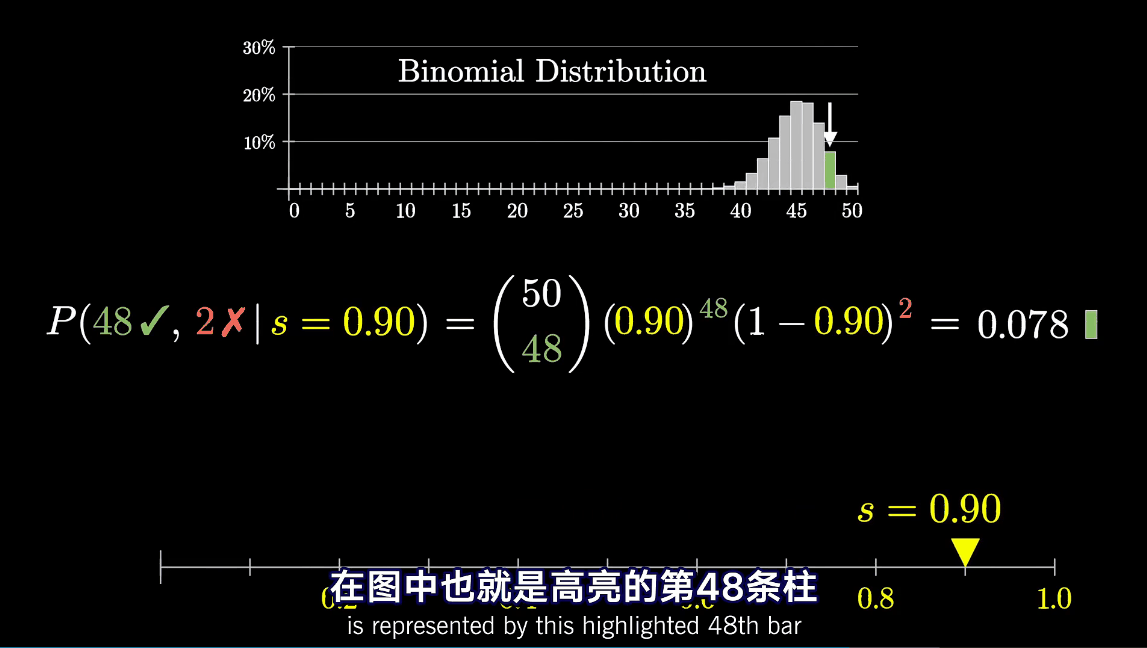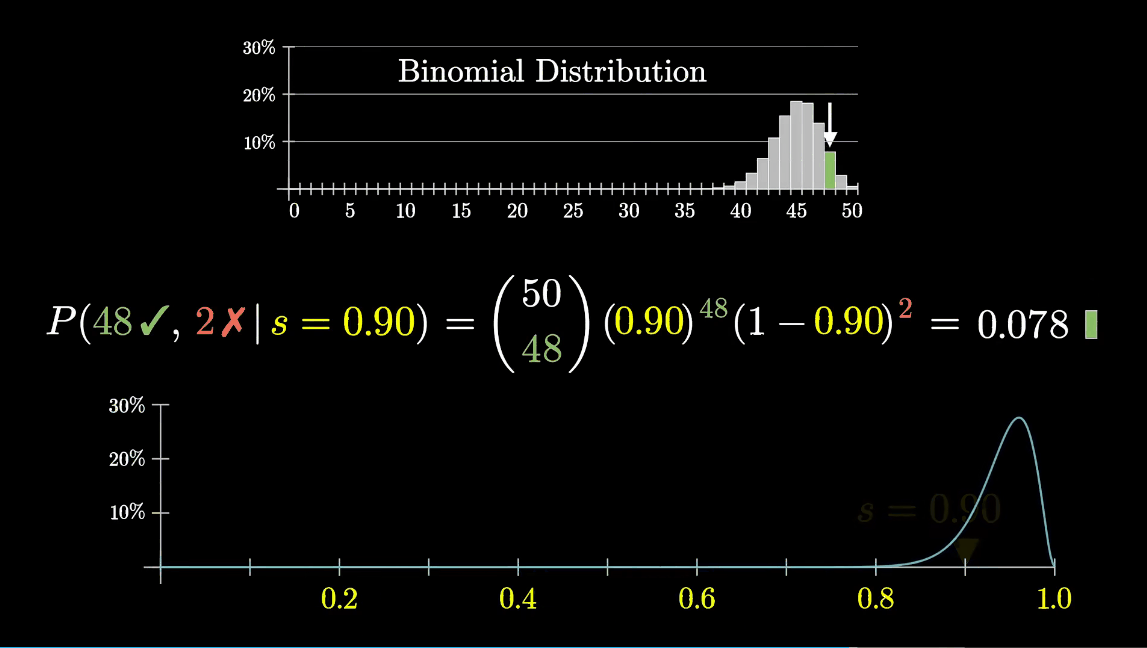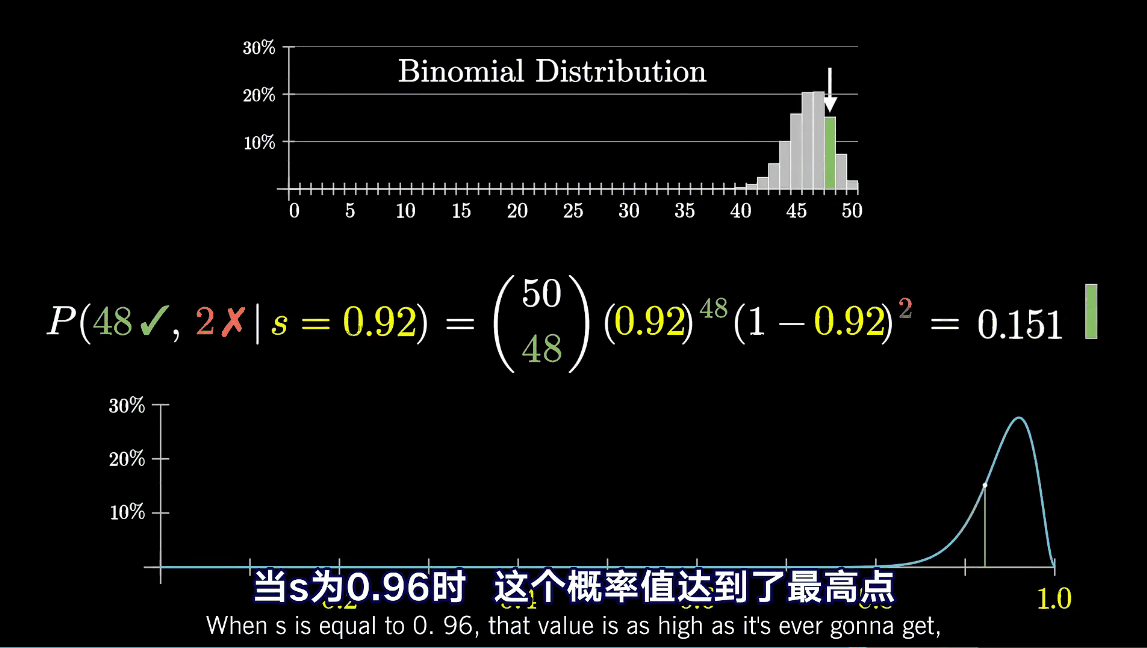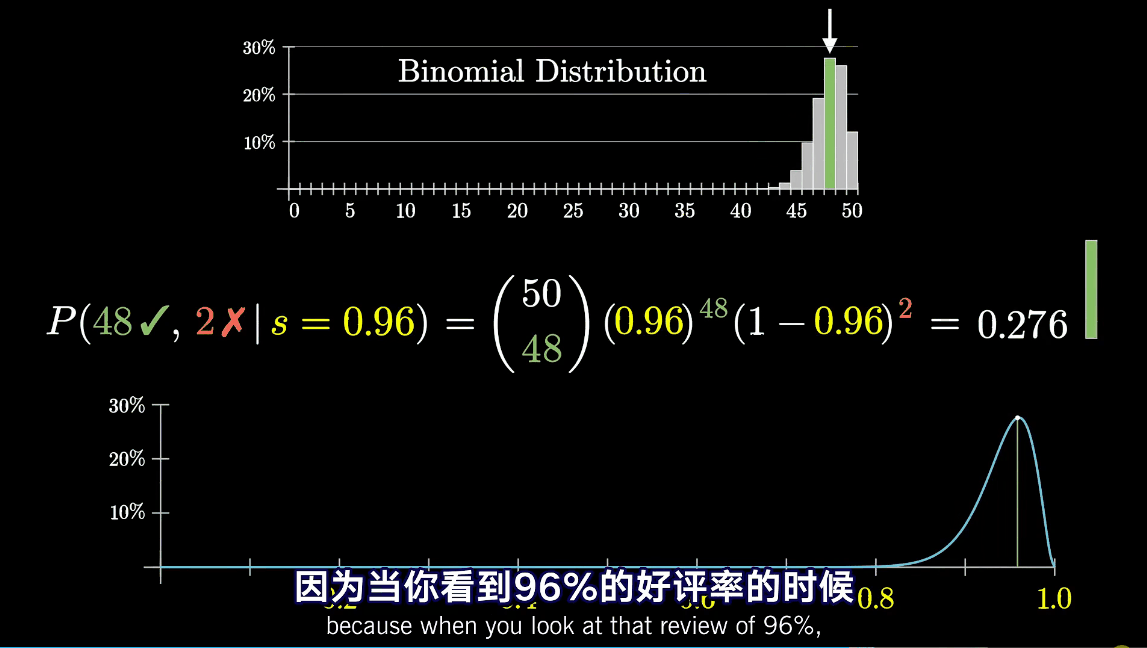
这个图说明,当s为0.96的时候,50条评论中出现48条好评的概率最大。
阶段小结:从这个例子中,我联想到了,先验概率,后验概率,最大似然(根据既定的事实推出概率模型),甚至联系到泊松分布。
这些貌似还和朴素贝叶斯有关,目前这部分的讨论就到这里吧,以后慢慢完成知识体系。
泊松分布
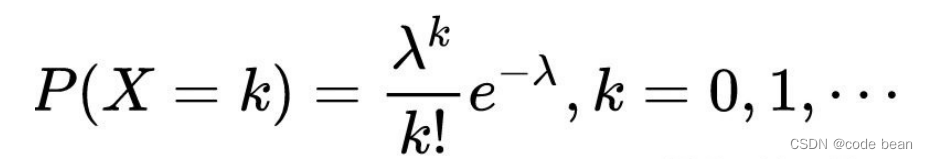
首先泊松分布是二项式分布的一种特殊形式,当二项式分布公式的p趋近0(很小),实验次数趋近无穷大,且n*p等于一个常量时,我们将得到泊松分布。泊松分布中的 “入”其实就是二项式分布中的n*p。
适用泊松分布的事件需要满足三个条件:
1 这个事件是一个小概率事件
2 事件独立互不影响
3 事件的概率稳定
将一定的时间无限划分,直至在时间上某事件最多发生一次。那么这段时间我称之为泊松分布的单位时间。
题目1: 目前一分钟钟来了3辆车,求一分钟来5辆车的概率?
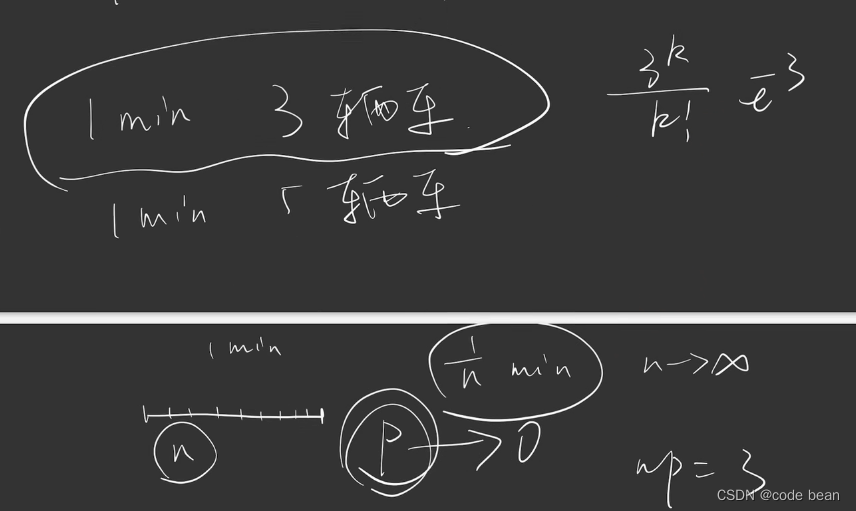
当“入”确定之后,这个图像就确定了,概率P随着K的变化而变化。而在二项分布中需要知道n和p
这个“入”的含义是,在单位时间内随机事件的平均发生率(没错就是np了np的含义就是期望/均值)
题目2: 新华书店,每周卖出4本新华字典,老板应该备多少新华字典?(未完成)
参考资料:
统计学与质量026 - 伯努利试验及概率方程 二项式分布 期望值与方差_哔哩哔哩_bilibili
概率的概率,第一部分--二项分布_哔哩哔哩_bilibili
泊松分布是怎么来的?应该怎么用?_哔哩哔哩_bilibili


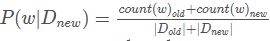



![[cryptoverse ctf 2022] cvctf](https://img-blog.csdnimg.cn/a6805ee635a243a7b4286b0d4f411df2.jpeg)