结构因果模型SCM

  结构因果模型（SCM）由内生变量$V$、外生变量$U$和映射函数$F$构成。因果的定义：若$Y$在$f_X$ 的定义域中，则$Y$是$X$的直接原因 ；如果$Y$是$X$的直接原因，或者是直接原因的原因，则$Y$是$X$的原因。
  $U$中的变量称为外生变量，它们属于模型的外部，不必解释它们变化的原因。$V$中的变量称为内生变量，模型中每一个内生变量都至少是一个外生变量的后代。外生变量没有祖先节点，不是内生变量的后代。

因果图的三种结构

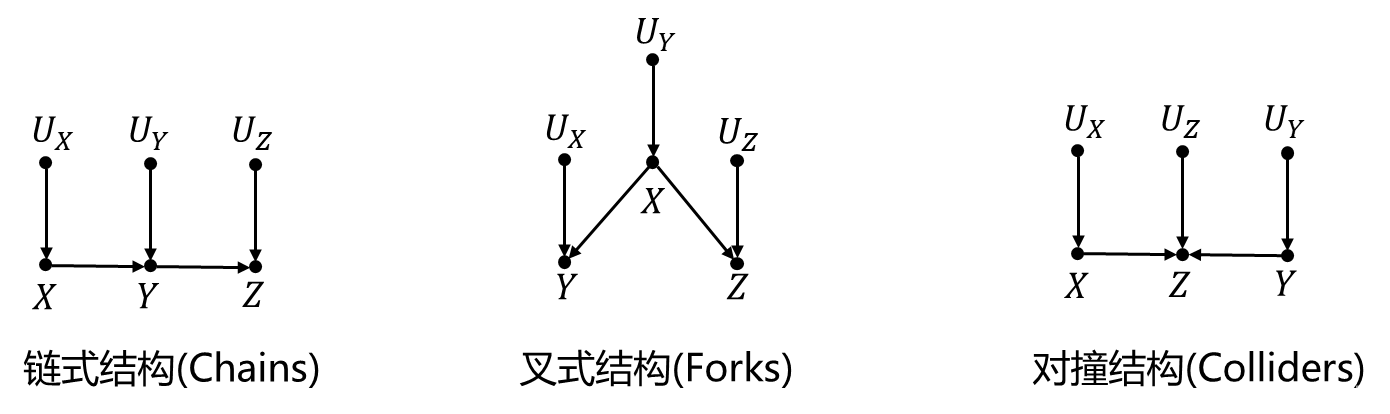
链式结构

1. 相关性： 链式结构中，信息从$X$经过$Y$流向$Z$，所以$X$和$Z$是相关的
2. 链式结构中的条件独立性： 如果变量$X$和变量$Z$之间只有一条单向路径，$Y$是截断这条路径的任何一组变量，则在$Y=y$的条件下，$X$和$Z$是独立的
3. 例：火灾$\to$烟雾$\to$烟雾警报，在统计的数据中查看“烟雾=1”的数据会发现，无论是否有火灾，一定会响警报，与火灾的值为0或者1无关，以中介为条件的情况下，火灾和烟雾警报独立

叉式结构

1. 相关性： 叉式结构中，信息从$X$流向$Y$和$Z$，所以$Y$和$Z$是相关的
2. 叉式结构中的条件独立性： 如果变量$X$是变量$Y$和$Z$的共因，并且变量$Y$和$Z$之间只有一条单向路径，则$Y$和$Z$在$X=x$的条件下是独立的
3. 例：鞋子尺码$\leftarrow$年龄$\to$阅读能力，小孩年龄大，一般鞋码长，阅读能力也更强，但是只看统计数据中“年龄=8岁”小孩的记录会发现，鞋子尺码和其阅读能力间是没有关系的

对撞结构

1. 相关性： 对撞结构中，变量$X$和$Y$都影响$Z$，但是信息没有从$Z$流向$X$或者$Y$，所以$X$和$Y$是独立的（假设没有其他的边）
2. 对撞结构中的条件独立性： 若$Z$是$X$和$Y$的对撞节点，且$X$和$Y$间只有一条路径，则$X$和$Y$是无条件独立的，若以$Z$或者$Z$的子孙节点为条件会让$X$和$Y$产生关联（以对撞节点为条件会使得该节点的父节点互相依赖）
3. 例：绩点$\to$奖学金$\leftarrow$活动分，查看获得奖学金的这些人，如果学习成绩不好，那么他们一定参加了很多活动才评上奖学金，参加活动和学习成绩产生了关联

$d$-分离

定义： 一条路径会被以一组节点$Z$时阻断，当且仅当：

1. 路径$p$包含链结构$A\to B\to C$或者分叉结构 $A\leftarrow B\to C$，且中间节点$B$在$Z$中（也就是以$B$为条件），或者
2. 路径$p$包含一个对撞结构$A\to B\leftarrow C$，且对撞节点$B$及其子孙节点都不在$Z$中
   
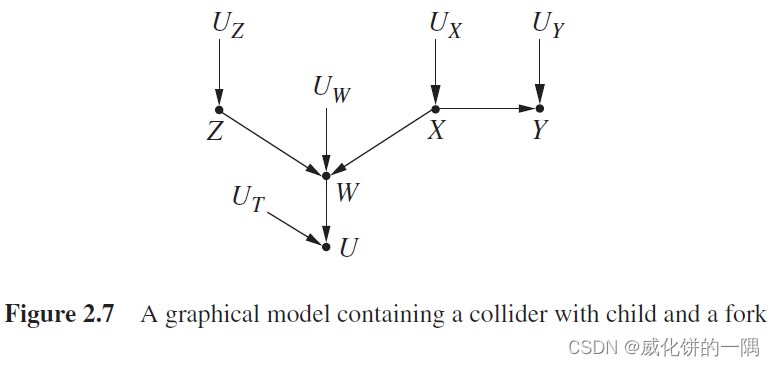
   例如，在条件集为空集时，$Z$与$X$是$d$-分离的（条件独立）；在条件集为$X$时，$W$与$Y$是$d$-分离的（条件独立）。

干预运算($do$-calculus)

  完全的随机对照试验可以解决很多问题，但是有的问题不适合用随机对照试验来解决，可以对变量进行干预，提取因果关系。需要区别的是，对一个变量进行干预和以该变量为条件是不一样的。当要干预图模型中的一个变量时，需要固定这个变量的值，也就是改变了系统，其他变量的值通常会因此发生变化。例如，可以发现干预冰淇淋销量，发现不会影响犯罪的数目，冰淇淋销量和犯罪率没有因果关系。干预是否接种疫苗，发现接种后，患病率下降了，二者存在因果关系。但是以一个变量为条件，不会做任何改变，只是在取统计数据时关注这个条件下的某个子集。“以变量为条件，改变的是我们对世界的看法，而不是世界本身”。

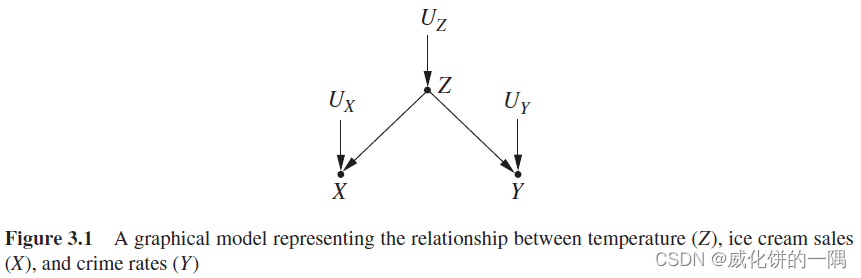
  上图显示了冰淇淋销量例子的图模型，$X$表示冰淇淋销量，$Y$表示犯罪率，$Z$表示温度。例如进行干预，降低冰淇淋销量，在图模型中干预$X$表示把指向$X$的所有边移除（如下图），然后对$X$进行赋值。$X$的值由干预时的赋值决定，与父节点无关，但是这个赋值操作会影响$X$的子节点。在干预后的图模型中可以发现，$X$和$Y$完全独立，二者不相关，没有因果关系。

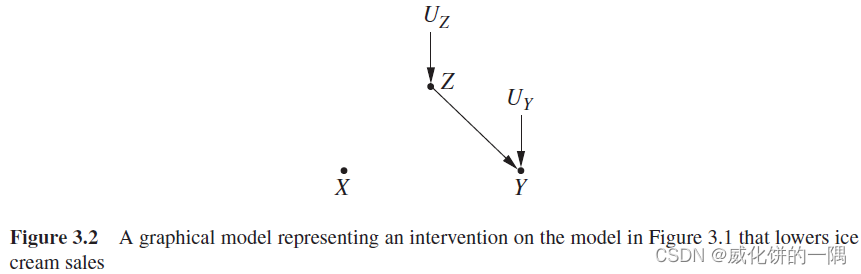
  在符号上，使用$do$运算来表示干预操作，变量$X$在干预情况下被赋值为$x$表示为$do(X=x)$。在$X=x$的条件下$Y=y$的概率为$P(Y=y|X=x)$，通过干预使得$X=x$的概率为$P(Y=y|do(X=x))$。$P(Y=y|X=x)$表示在数据中观察，$X=x$的这些个体组成的群体的$Y$的分布；$P(Y=y|do(X=x))$表示的是如果所有个体都把$X$的值固定为$X=x$时，总体中$Y$的分布。

平均因果效应ACE

  平均因果效应ACE可以用来衡量某个操作带来的效果，例如为了确定药物的有效性，假设干预操作是让整个人群都服药或者不服药，然后比较两种干预下的健康数值。用$do(X=1)$表示让所有人服药，用$do(X=0)$表示让所有人不服药，二者的差异为平均因果效应ACE。
$$ACE=P(Y=1|do(X=1))-P(Y=1|do(X=0))$$

后门准则与调整公式

  假如要计算下图中的$P(Y=y|do(X=x))$，存在混杂（$Z$是$X$和$Y$的共因），因为满足后门准则，因果效应是可识别的，具体可以使用调整公式来进行计算。

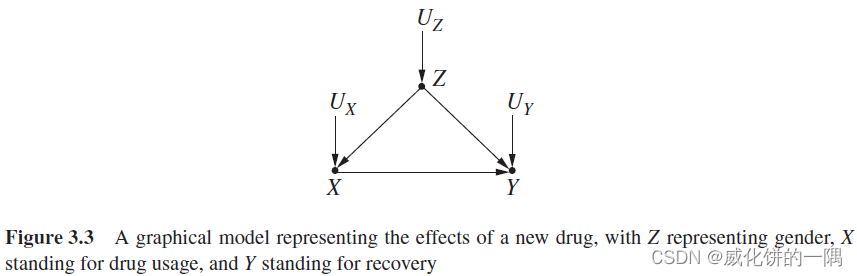
  后门准则： 给定有向无环图中的一组有序变量$(X,Y)$，如果变量集合$Z$满足：$Z$中没有$X$的后代节点，且$Z$阻断了$X$与$Y$直接的每条含有指向$X$的边的路径(后门路径)，则称$Z$满足关于$(X,Y)$的后门准则。
  需要注意的是$X\to Y$表示$X$到$Y$有前门路径，$X\leftarrow Y$表示$X$到$Y$有后门路径，反的箭头也表示是路径。。。。。
  如果变量集合$Z$满足$(X,Y)$的后门准则，那么$X$对$Y$的因果效应可以使用调整公式计算（证明见参考文献）：
$$P(Y=y|do(X=x))=\sum _{z}P(Y=y|X=x,Z=z)P(Z=z)$$

前门准则与前门校正公式

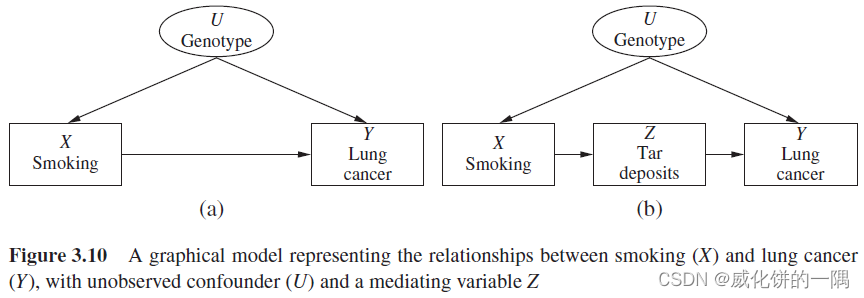
  对于上图(a)，存在一个不可观测的混杂因子$U$，是$X$和$Y$的共因，要估计$X$对$Y$的因果效应就不能用后门准则了，因为没有$U$的统计信息。但是，如果额外有一个可以观测的变量$Z$位于$X$和$Y$之间，作为中介变量，这种情况下$X$和$Y$的因果效应是可识别的，满足前门准则，可以使用前门校正公式来计算。
  前门准则： 变量集合$Z$被称为满足关于有序变量对$(X,Y)$的前门准则，当：
    1. $Z$切断了所有$X$到$Y$的有向路径($X\to ...\to Y$)
    2. $X$到$Z$没有后门路径
    3. 所有$Z$到$Y$的后门路径都被$X$阻断

  如果$Z$满足关于有序变量对$(X,Y)$的前门准则，并且$P(x,z)>0$，那么$X$对$Y$的因果效应是可识别的，且由下式计算：
$$P(Y=y|do(x))=\sum _{z}P(z|x)\sum _{x^{\prime }}P(y|x^{\prime },z)P(x^{\prime })$$

工具变量

  假如存在无法观测的混杂因子，不满足前门准则，要识别$X$到$Y$的因果效应，可以考虑引入工具变量，借助来计算因果效应。
  一个变量𝑍称为工具变量，满足三个性质 :

1. 相关性：$R$对$X$有因果效应 （Relevance）
2. $R$对$X$的因果效应都由$X$中介 （Exclusion Restriction）
3. 工具变量不存在混杂（不存在到$Y$未被阻断的后门路径）（Instrumental Unconfoundedness）

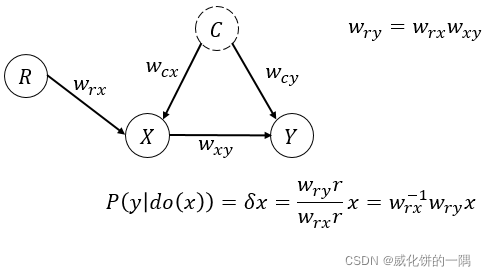
  例如上图中，假设是线性模型，$X$对$Y$的因果效应是系数，也就是$\delta$，混杂效应$\alpha$不可观测，引入工具变量$R$。如果求$R$对$Y$的平均因果效应，可以得到
$$\begin{array}{rl}& \mathbb{E}[Y|R=1]-\mathbb{E}[Y|R=0]\\ & =\mathbb{E}[\delta X+\alpha C|R=1]-\mathbb{E}[\delta X+\alpha C|R=1](Y=\delta X+\alpha C)\\ & =\delta (\mathbb{E}[X|R=1]-E(X|R=0))+\alpha (\mathbb{E}[C|R=1]-\mathbb{E}[C|R=0])\\ & =\delta (\mathbb{E}[X|R=1]-E(X|R=0))(unconfoundedness)\end{array}$$
  所以可以求出来因果效应为
$$\delta =\frac{\mathbb{E}[Y|R=1]-\mathbb{E}[Y|R=0]}{\mathbb{E}[X|R=1]-\mathbb{E}[X|R=0]}$$
  如果是下面的图，可以得到对应的结论：

参考文献

上面写的仅仅是个人理解，不一定正确，参考文献更为严谨
【1】因果推理网课，https://www.bradyneal.com/causal-inference-course
【2】因果推理课本，Causal Inference in Statistics：A Primer
【3】因果推理课本中文翻译版，统计因果推理入门
【4】因果推理知乎专栏，因果关系之梯，by望止洋，https://www.zhihu.com/column/c_1217887302124773376