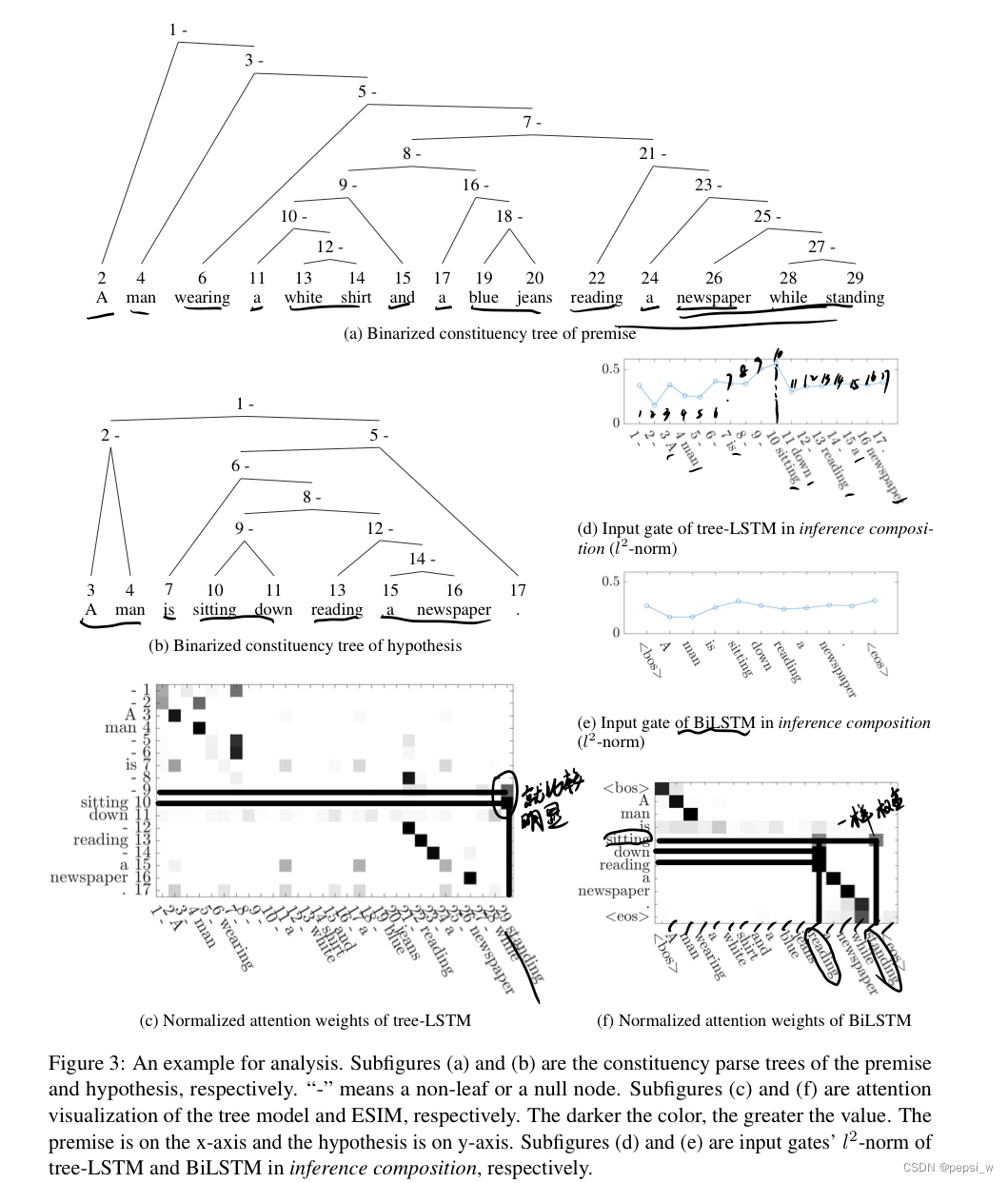
theta: org parameter, theta_P: variational parameter
1. goal: 估计p(z|x)
2. 找p(x|theta)likelihood的lower bound,再max这个lower bound 就能找到 p(z|x)的近似分布q(z|theta_P)
3. 找complete likelihood ln[p(x,z)]的关于qj j!=i的期望
4. incomplete likelihood的lower bound 应该是 q(z)*ln p(x,z)/q(z)这个玩意, complete likelihood 乘除q(z)
ref:http://www.crescentmoon.info/?p=709#more-709
问题描述
变分推断是一类用于贝叶斯估计和机器学习领域中近似计算复杂(intractable)积分的技术,它广泛应用于各种复杂模型的推断。本文是学习PRML第10章的一篇笔记,错误或不足的地方敬请指出。
先给出问题描述。记得在上一篇EM的文章中,我们有一个观察变量 X={x{1},…,x{m}} 和隐藏变量 Z={z{1},…,z{m}} , 整个模型 p(X,Z) 是个关于变量 X,Z 的联合分布,我们的目标是得到后验分布 P(Z|X) 的一个近似分布。This is our goal
在之前介绍过Gibbs Sampling这一类Monte Carlo算法,它们的做法就是通过抽取大量的样本估计真实的后验分布。而变分推断不同,与此不同的是,变分推断限制近似分布的类型,从而得到一种局部最优,但具有确定解的近似后验分布。
之前在EM算法中我们有似然的式子如下:
其中
这里公式中不再出现参数 θ ,因为参数不再是固定的值,而变成了随机变量,所以也是隐藏变量,包括在 Z 之内了。
因为这里假设参数theta是给定的,所以lnp(X|theta)是定值,所以要min KL(q||p),只需要maxL(q) 这个incomplete likelihood lower bound即可。
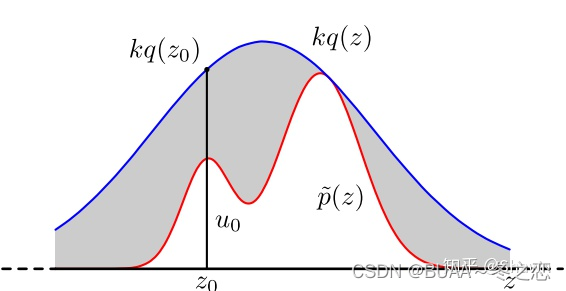
这里的KL散度 KL(q||p) 描述了估计分布与真实分布的差别。当 KL(q||p)=0 时,俩分布就是相同的。但是因为我们不知道真实的后验分布是啥,所以直接最小化KL是做不到的,所以我们通过最大化 L(q) 来达到这个目的可以认为 L(q) 越大,则模型对数据拟合程度越好。要注意到 lnp(X)≥L(q) 始终成立,所以 L(q) 被称作证据下界(evidence lower bound),见图1。

为了极大化 L(q) ,我们需要选择合适的函数 q ,使其便于计算。要注意到 L(q) 并非普通的函数,而是以函数 q 为自变量的函数,这就是泛函。泛函可以看成是函数概念的推广,而变分方法是处理泛函的数学领域,和处理函数的普通微积分相对。变分法最终寻求的是极值函数:它们使得泛函取得极大或极小值。
条件独立假设
如果参数之间具有相互依赖关系(mutually dependent),求积分时会比较麻烦。所以我们为 q(Z) 的分布加一个限制条件,将 Z 分为 M 组变量,组与组之间变量相互独立,这样 q 的分布就可以分解为
要注意我们对每个 q(Zi) 的函数形式并没有做任何限制。这种将 q 分解的方法叫做平均场理论(mean field theory),主要基于基于系统中个体的局部相互作用可以产生宏观层面较为稳定的行为这个物理思想。
求解过程
根据以上假设,我们来最大化下界 L(q) ,因为假设 qi(Zi) 分布之间都是独立的,所以我们依次轮流来优化,以 qj(Zj) 为例(为了简单起见,缩写为 qj )。
这里我们定义一个新分布 lnp~(X,Zj) 为
我们发现它刚好是除去与 qj 分布相关的 zj 之后原似然的期望值,有
然后看式(5)的最后部分,就是 qj(Zj) 和 lnp~(X,Zj) 的KL散度的负值,这里我们固定 qi≠j 不变,那么最大化 L(q) 就变成了最小化这个KL散度,而KL 散度的最小值在 qj(Zj)=lnp~(X,Zj) 时取到。所以,最优解 q∗j(Zj) 为
另加的这个C是为了归一化整个分布,有 C=∫exp(Ei≠j[lnp(X,Z)])dZj 。然后依次更新其他 Zj ,最终相互迭代达到稳定。
变分下界
我们也可以直接衡量模型的下界。在实际应用中,变分下界可以直接判断算法是否收敛,也可以通过每次迭代都不会降低这一点来判断算法推导和实现的部分是否存在问题。
值得一提的是,如果我们能知道变分后验每个因子的函 数 形式的话,我们还有另一种估计参数的方法,这个详见 例子 。
变分推断和Gibbs Sampling之间的联系
变分推断和Gibbs sampling其实挺相似的:
- 在Gibbs Sampling中,我们从条件分布 P(Zj|Z¬j) 中抽样。
- 在变分推断中,我们迭代 Zj 的分布 Q(Zj)∝1Cexp{Ei≠j[lnp(X,Z)]}
参考:
1.《Pattern_Recognition_and_Machine_Learning》第10章
2.http://en.wikipedia.org/wiki/Variational_Bayesian_methods