一、什么是变分推断
假设在一个贝叶斯模型中, x x x为一组观测变量, z z z为一组隐变量(参数也看做随机变量,包含在 z z z中),则推断问题为计算后验概率密度 P = ( z ∣ x ) P=(z|x) P=(z∣x)。根据贝叶斯公式,有:
p ( z ∣ x ) = p ( x , z ) p ( x ) = p ( x , z ) ∫ p ( x , z ) d z p(z|x)=\frac{p(x,z)}{p(x)}=\frac{p(x,z)}{\int p(x,z)dz} p(z∣x)=p(x)p(x,z)=∫p(x,z)dzp(x,z)
但是在实际应用中,可能由于积分没有闭式解,或者是指数级的计算复杂度等原因,导致计算上面公式中的积分往往是不可行的。变分推断就是用来解决这个问题的。
变分推断是变分法在推断问题中的应用,既然无法直接求得后验概率密度 p ( z ∣ x ) p(z|x) p(z∣x),那我们可以寻找一个简单的分布 q ∗ ( z ) q^*(z) q∗(z)来近似后验概率密度 p ( z ∣ x ) p(z|x) p(z∣x),这就是变分推断的思想。借此,我们将推断问题转换为一个泛函优化问题:
q ∗ ( z ) = arg min q ( z ) ∈ Q K L ( q ( z ) ∣ ∣ p ( z ∣ x ) ) (1) q^*(z)=\arg\min_{q(z)\in Q}KL(q(z)||p(z|x))\tag{1} q∗(z)=argq(z)∈QminKL(q(z)∣∣p(z∣x))(1)
其中 Q Q Q为候选的概率分布族。但是又出现了一个新的问题:我们已经知道后验概率密度 p ( z ∣ x ) p(z|x) p(z∣x)难以计算,所以上式中的KL散度本身也是无法计算的!这时,需要借助于证据下界ELBO。
ELBO
ELBO,全称为 Evidence Lower Bound,即证据下界。这里的证据指数据或可观测变量的概率密度。
假设 x = x 1 : n x=x_{1:n} x=x1:n表示一系列可观测数据集, z = z 1 : m z=z_{1:m} z=z1:m为一系列隐变量(latent variables)。则可用 p ( z , x ) p(z,x) p(z,x)表示联合概率, p ( z ∣ x ) p(z∣x) p(z∣x)为条件概率, p ( x ) p(x) p(x)为证据。
那么,贝叶斯推理需要求解的就是条件概率,即: p ( z ∣ x ) = p ( x , z ) p ( x ) p(z|x)=\frac{p(x,z)}{p(x)} p(z∣x)=p(x)p(x,z)
(1)式中的KL散度可以表示为 K L ( q ( z ) ∣ ∣ p ( z ∣ x ) ) = ∫ q ( z ) log q ( z ) p ( z ∣ x ) d z KL(q(z)||p(z|x))=\int q(z)\log\frac{q(z)}{p(z|x)}dz KL(q(z)∣∣p(z∣x))=∫q(z)logp(z∣x)q(z)dz其中, x x x为可观测数据集, z z z为未知变量,下面将公式继续变形:
∫ q ( z ) log q ( z ) p ( z ∣ x ) d z = − ∫ q ( z ) log p ( z ∣ x ) q ( z ) d z = − ∫ q ( z ) log p ( x , z ) q ( z ) p ( x ) d z = − ∫ q ( z ) log p ( x , z ) d z + ∫ q ( z ) log q ( z ) d z + ∫ q ( z ) log p ( x ) d z \begin{aligned}\int q(z)\log\frac{q(z)}{p(z|x)}dz&=-\int q(z)\log\frac{p(z|x)}{q(z)}dz\\&=-\int q(z)\log\frac{p(x,z)}{q(z)p(x)}dz\\&=-\int q(z)\log p(x,z)dz+\int q(z)\log q(z)dz+\int q(z)\log p(x)dz\end{aligned} ∫q(z)logp(z∣x)q(z)dz=−∫q(z)logq(z)p(z∣x)dz=−∫q(z)logq(z)p(x)p(x,z)dz=−∫q(z)logp(x,z)dz+∫q(z)logq(z)dz+∫q(z)logp(x)dz其中, ∫ q ( z ) d z = 1 \int q(z)dz=1 ∫q(z)dz=1进而可以转化成: = − ∫ q ( z ) log p ( x , z ) d z + ∫ q ( z ) log q ( z ) d z + log p ( x ) =-\int q(z)\log p(x,z)dz+\int q(z)\log q(z)dz+\log p(x) =−∫q(z)logp(x,z)dz+∫q(z)logq(z)dz+logp(x)令 L ( q ( z ) ) = ∫ q ( z ) log p ( x , z ) d z − ∫ q ( z ) log q ( z ) d z L(q(z))=\int q(z)\log p(x,z)dz-\int q(z)\log q(z)dz L(q(z))=∫q(z)logp(x,z)dz−∫q(z)logq(z)dz,
则有 K L ( q ( z ) ∣ ∣ p ( z ∣ x ) ) = − L ( q ( z ) ) + log p ( x ) KL(q(z)||p(z|x))=-L(q(z))+\log p(x) KL(q(z)∣∣p(z∣x))=−L(q(z))+logp(x)从这个公式可以发现, log p ( x ) \log p(x) logp(x)不涉及参数(数据似然),因此在最小化 K L ( q ( z ) ∣ ∣ p ( z ∣ x ) ) KL(q(z)||p(z|x)) KL(q(z)∣∣p(z∣x))时可以忽略。那么,最小化 K L ( q ( z ) ∣ ∣ p ( z ∣ x ) ) KL(q(z)||p(z|x)) KL(q(z)∣∣p(z∣x))便转化成了最大化 L ( q ( z ) ) L(q(z)) L(q(z))。
因为 K L ( q ( z ) ∣ ∣ p ( z ∣ x ) ) ≥ 0 KL(q(z)||p(z|x))\geq 0 KL(q(z)∣∣p(z∣x))≥0,即: − L ( q ( z ) ) + log p ( x ) ≥ 0 -L(q(z))+\log p(x)\geq 0 −L(q(z))+logp(x)≥0进而可以得到: log p ( x ) ≥ L ( q ( z ) ) \log p(x)\geq L(q(z)) logp(x)≥L(q(z))因此,可以将 L ( q ( z ) ) L(q(z)) L(q(z))堪称 log p ( x ) \log p(x) logp(x)的下界,这个下界也称之为ELBO(evidence lower bound),那么最小化 K L ( q ( z ) ∣ ∣ p ( z ∣ x ) ) KL(q(z)||p(z|x)) KL(q(z)∣∣p(z∣x)),可以看成最大化下界的问题。
另外,从公式中可以看到,KL散度是 L ( q ( z ) ) L(q(z)) L(q(z))与 log p ( x ) \log p(x) logp(x)的误差,当然误差越小越好。
根据以上结果,最新的目标函数转化成了 q ∗ ( z ) = arg max q ( z ) ∈ Q L ( q ( z ) ) = arg max q ( z ) ∈ Q ∫ z q ( z ) log p ( x , z ) d z ⏟ ( a ) − ∫ z q ( z ) log q ( z ) d z ⏟ ( b ) (2) \begin{aligned}q^*(z)&=\arg\max_{q(z)\in Q}L(q(z))\\&=\arg\max_{q(z)\in Q}\underbrace{\int_z q(z)\log p(x,z)dz}_{(a)}-\underbrace{\int_z q(z)\log q(z)dz}_{(b)}\tag{2}\end{aligned} q∗(z)=argq(z)∈QmaxL(q(z))=argq(z)∈Qmax(a) ∫zq(z)logp(x,z)dz−(b) ∫zq(z)logq(z)dz(2)至此,我们已经解决了KL散度无法求解的问题,将泛函优化问题转换为寻找一个简单分布 q ∗ ( z ) q^*(z) q∗(z)来最大化证据下界 L ( q ( z ) ) L(q(z)) L(q(z))。
二、基于平均场理论的变分推断
在变分推断中,候选分布族 Q Q Q的复杂性决定了优化问题的复杂性。一个通常的选择是平均场分布族,即 z z z可以拆分成多组相互独立的变量,有: q ( z ) = ∏ i = 1 M q i ( z i ) (3) q(z)=\prod_{i=1}^Mq_i(z_i)\tag{3} q(z)=i=1∏Mqi(zi)(3)其中 z i z_i zi是隐变量的子集,可以是单变量,也可以是一组多元变量。
下面我们分布(3)把将代入(2)中的(a)和(b),看看 L ( q ( z ) ) L(q(z)) L(q(z))最后的模样,其中假设我们想先求 q j ( z j ) q_j(z_j) qj(zj),将其它组的 q ∖ j ( z ∖ j ) q_{\setminus j}(z_{\setminus j}) q∖j(z∖j)当作常量:
2.1、求解(a)
我们首先求解(a):
( a ) = ∫ z q ( z ) log p ( x , z ) d z = ∫ z ∏ i = 1 M q i ( z i ) log p ( x , z ) d z = ∫ z j q j ( z j ) ( ∫ z ∖ j ∏ i ≠ j q i ( z i ) log p ( x , z ) d z ∖ j ) d z j = ∫ z j q j ( z j ) E ∏ i ≠ j q i ( z i ) [ log p ( x , z ) ] d z j = ∫ z j q j ( z j ) log p ^ ( x , z j ) d z j \begin{aligned}(a)&=\int_z q(z)\log p(x,z)dz\\&=\int_z\prod_{i=1}^M q_i(z_i)\log p(x,z)dz\\&=\int_{z_j}q_j(z_j)(\int_{z_{\setminus j}}\prod_{i\neq j}q_i(z_i)\log p(x,z)dz_{\setminus j})dz_j\\&=\int_{z_j}q_j(z_j)E_{\prod_{i\neq j}q_i(z_i)}[\log p(x,z)]dz_j\\&=\int_{z_j}q_j(z_j)\log \hat{p}(x,z_j)dz_j\end{aligned} (a)=∫zq(z)logp(x,z)dz=∫zi=1∏Mqi(zi)logp(x,z)dz=∫zjqj(zj)(∫z∖ji=j∏qi(zi)logp(x,z)dz∖j)dzj=∫zjqj(zj)E∏i=jqi(zi)[logp(x,z)]dzj=∫zjqj(zj)logp^(x,zj)dzj在最后一步中,我们把期望 E ∏ i ≠ j q i ( z i ) [ log p ( x , z ) ] E_{\prod_{i\neq j}q_i(z_i)}[\log p(x,z)] E∏i=jqi(zi)[logp(x,z)]记为 log p ^ ( x , z j ) \log \hat{p}(x,z_j) logp^(x,zj)
2.2、求解(b)
接着,我们求解(b):
( b ) = ∫ z q ( z ) log q ( z ) d z = ∫ z ∏ i = 1 M q i ( z i ) ∑ j = 1 M log q j ( z j ) d z (4) \begin{aligned}(b)&=\int_z q(z)\log q(z)dz\\&=\int_z\prod_{i=1}^M q_i(z_i)\sum_{j=1}^M\log q_j(z_j)dz\tag{4}\end{aligned} (b)=∫zq(z)logq(z)dz=∫zi=1∏Mqi(zi)j=1∑Mlogqj(zj)dz(4)我们取 ∑ \sum ∑符号中的第一项出来,看看有没有什么规律可以帮助我们化简:
∫ z ∏ i = 1 M q i ( z i ) log q 1 ( z 1 ) d z = ∫ z q 1 ( z 1 ) log q 1 ( z 1 ) q 2 ( z 2 ) q 2 ( z 3 ) ⋯ ⋯ q M ( z M ) d z = ∫ z 1 q 1 ( z 1 ) log q 1 ( z 1 ) d z 1 ∫ z 2 q 2 ( z 2 ) d z 2 ⏟ = 1 ∫ z 3 q 3 ( z 3 ) d z 3 ⏟ = 1 ⋯ ⋯ ∫ z M q M ( z M ) d z M ⏟ = 1 = ∫ z 1 q 1 ( z 1 ) log q 1 ( z 1 ) d z 1 \begin{aligned}\int_z\prod_{i=1}^M q_i(z_i)\log q_1(z_1)dz&=\int_z q_1(z_1)\log q_1(z_1)q_2(z_2)q_2(z_3)\cdots\cdots q_M(z_M)dz\\&=\int_{z_1} q_1(z_1)\log q_1(z_1)dz_1\underbrace{\int_{z_2}q_2(z_2)dz_2}_{=1}\underbrace{\int_{z_3}q_3(z_3)dz_3}_{=1}\cdots\cdots\underbrace{\int_{z_M}q_M(z_M)dz_M}_{=1}\\&=\int_{z_1} q_1(z_1)\log q_1(z_1)dz_1\end{aligned} ∫zi=1∏Mqi(zi)logq1(z1)dz=∫zq1(z1)logq1(z1)q2(z2)q2(z3)⋯⋯qM(zM)dz=∫z1q1(z1)logq1(z1)dz1=1 ∫z2q2(z2)dz2=1 ∫z3q3(z3)dz3⋯⋯=1 ∫zMqM(zM)dzM=∫z1q1(z1)logq1(z1)dz1综上,(4)式可继续化简为:
( b ) = ∫ z ∏ i = 1 M q i ( z i ) ∑ j = 1 M log q j ( z j ) d z = ∑ i = 1 M ∫ z i q i ( z i ) log q i ( z i ) d z i = ∫ z j q j ( z j ) log q j ( z j ) d z j + C \begin{aligned}(b)&=\int_z\prod_{i=1}^M q_i(z_i)\sum_{j=1}^M\log q_j(z_j)dz\\&=\sum_{i=1}^M\int_{z_i} q_i(z_i)\log q_i(z_i)dz_i\\&=\int_{z_j} q_j(z_j)\log q_j(z_j)dz_j+C\end{aligned} (b)=∫zi=1∏Mqi(zi)j=1∑Mlogqj(zj)dz=i=1∑M∫ziqi(zi)logqi(zi)dzi=∫zjqj(zj)logqj(zj)dzj+C
2.3、求解ELBO
至此,(a)、(b)我们都求出来了,现在回到证据下界 L ( q ( z ) ) L(q(z)) L(q(z)):
L ( q ( z ) ) = ( a ) − ( b ) = ∫ z j q j ( z j ) log p ^ ( x , z j ) d z j − ∫ z j q j ( z j ) log q j ( z j ) d z j + C = ∫ z j q j ( z j ) log p ^ ( x , z j ) q j ( z j ) + C = − K L ( q j ( z j ) ∣ ∣ p ^ ( x , z j ) ) + C \begin{aligned}L(q(z))&=(a)-(b)\\&=\int_{z_j}q_j(z_j)\log \hat{p}(x,z_j)dz_j-\int_{z_j} q_j(z_j)\log q_j(z_j)dz_j+C\\&=\int_{z_j}q_j(z_j)\log\frac{\hat{p}(x,z_j)}{q_j(z_j)}+C\\&=-KL(q_j(z_j)||\hat{p}(x,z_j))+C\end{aligned} L(q(z))=(a)−(b)=∫zjqj(zj)logp^(x,zj)dzj−∫zjqj(zj)logqj(zj)dzj+C=∫zjqj(zj)logqj(zj)p^(x,zj)+C=−KL(qj(zj)∣∣p^(x,zj))+C由于 − K L ( q j ( z j ) ∣ ∣ p ^ ( x , z j ) ) ≤ 0 -KL(q_j(z_j)||\hat{p}(x,z_j))\leq 0 −KL(qj(zj)∣∣p^(x,zj))≤0,因此如果我们想令 L ( q ( z ) ) L(q(z)) L(q(z))最大,则 K L ( q j ( z j ) ∣ ∣ p ^ ( x , z j ) ) = 0 KL(q_j(z_j)||\hat{p}(x,z_j))=0 KL(qj(zj)∣∣p^(x,zj))=0,即: q j ∗ ( z j ) = p ^ ( x , z j ) = e x p { E ∏ i ≠ j q i ( z i ) [ log p ( x , z ) ] } (5) q^*_j(z_j)=\hat{p}(x,z_j)=exp\{E_{\prod_{i\neq j}q_i(z_i)}[\log p(x,z)]\}\tag{5} qj∗(zj)=p^(x,zj)=exp{E∏i=jqi(zi)[logp(x,z)]}(5)从(5)式可知, q j ∗ ( z j ) q^*_j(z_j) qj∗(zj)的计算依赖于其他隐变量,因此我们采用坐标上升法,迭代地优化每个 q j ∗ ( z j ) , j = 1 , 2 , ⋯ , M q^*_j(z_j),j=1,2,\cdots,M qj∗(zj),j=1,2,⋯,M。通过不断地循环(5),证据下界 L ( q ( z ) ) L(q(z)) L(q(z))会收敛到一个局部最优值。
三、基于随机梯度的变分推断
上面提到的基于平均场理论的变分推断,最终导出了坐标上升的方法,但是平均场假设太强了,需要假设各组 z z z之间是相互独立的,这在例如玻尔兹曼机等情况下是不成立的,而且(5)式中的积分有时候也十分难算。
我们知道,常见的优化方法除了坐标上升,还有梯度上升,那么我们能否基于随机梯度来得到变分推断的另外一种方法,改进基于平均场理论的变分推导的算法缺点呢?
3.1、蒙特卡洛采样方法
首先简单介绍一下蒙特卡洛采样方法。
3.1.1、蒙特卡洛的概念
蒙特卡洛原来是一个赌场的名称,用它作为名字大概是因为蒙特卡洛方法是一种随机模拟的方法,这很像赌博场里面的扔骰子的过程。最早的蒙特卡洛方法都是为了求解一些不太好求解的求和或者积分问题
例如下图是一个经典的用蒙特卡洛求圆周率的问题,用计算机在一个正方形之中随机地生成点,计数有多少点落在1/4圆之中,这些点的数目除以总的点数目即圆的面积,根据圆面积公式即可求得圆周率
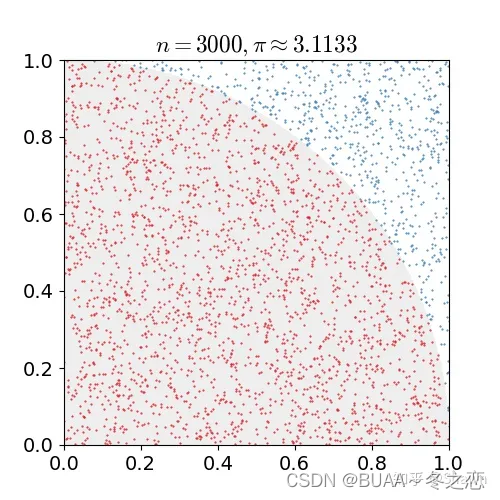
蒙特卡洛算法的另一个应用是求积分,某些函数的积分不好求,我们可以按照下面的方法将这个函数进行分解,之后转化为求期望与求均值的问题 ∫ a b h ( x ) d x = ∫ a b f ( x ) p ( x ) d x = E p ( x ) [ f ( x ) ] \int_a^bh(x)dx=\int_a^bf(x)p(x)dx=E_{p(x)}[f(x)] ∫abh(x)dx=∫abf(x)p(x)dx=Ep(x)[f(x)]从分布 p ( x ) p(x) p(x)采样大量样本点 x 1 , x 2 , ⋯ , x n x_1,x_2,\cdots,x_n x1,x2,⋯,xn,这些样本符合分布 p ( x ) p(x) p(x) E p ( x ) [ f ( x ) ] = 1 n ∑ f ( x i ) E_{p(x)}[f(x)]=\frac{1}{n}\sum f(x_i) Ep(x)[f(x)]=n1∑f(xi)最终使用蒙特卡洛的方法求得积分。
3.1.2、蒙特卡洛采样方法
对某一种概率分布 p ( x ) p(x) p(x)进行蒙特卡洛采样的方法主要分为直接采样、拒绝采样与重要性采样三种,下面分别予以介绍
直接采样
直接采样的方法是根据概率分布进行采样。对一个已知概率密度函数与累积概率密度函数的概率分布,我们可以直接从累积分布函数(cdf)进行采样
如下图所示是高斯分布的累积概率分布函数,可以看出函数的值域是 ( 0 , 1 ) (0, 1) (0,1),我们可以从 U ( 0 , 1 ) U(0, 1) U(0,1)均匀分布中进行采样,再根据累积分布函数的反函数计算对应的 x x x,这样就获得了符合高斯分布的 N N N个粒子
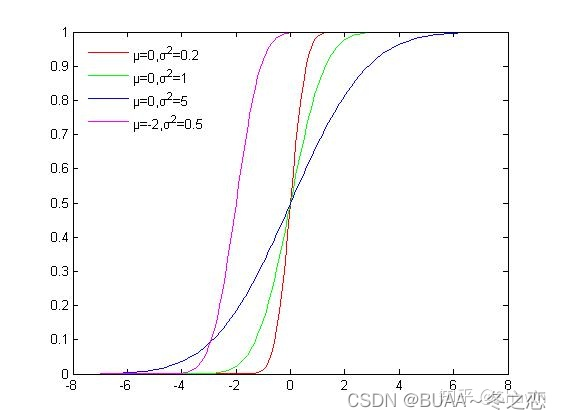
使用累积分布函数进行采样看似简单,但是由于很多分布我们并不能写出概率密度函数与累积分布函数,所以这种方法的适用范围较窄。
接受-拒绝采样
对于累积分布函数未知的分布,我们可以采用接受-拒绝采样。如下图所示, p ( z ) p(z) p(z)是我们希望采样的分布, q ( z ) q(z) q(z)是我们提议的分布(proposal distribution),令 k q ( z ) > p ( z ) kq(z)>p(z) kq(z)>p(z),我们首先在 k q ( z ) kq(z) kq(z)中按照直接采样的方法采样粒子,接下来判断这个粒子落在途中什么区域,对于落在灰色区域的粒子予以拒绝,落在红线下的粒子接受,最终得到符合 p ( z ) p(z) p(z)的 N N N个粒子
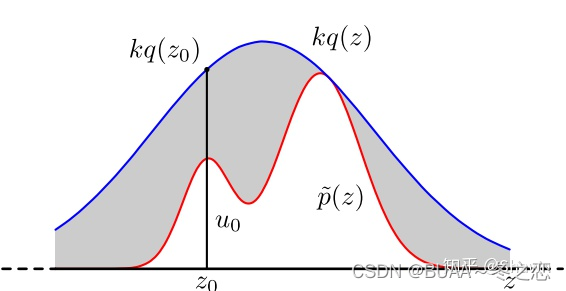
重要性采样
接受-拒绝采样完美的解决了累积分布函数不可求时的采样问题。但是接受拒绝采样非常依赖于提议分布(proposal distribution)的选择,如果提议分布选择的不好,可能采样时间很长却获得很少满足分布的粒子。而重要性采样就解决了这一问题
直接采样与接受-拒绝采样都是假设每个粒子的权重相等,而重要性采样则是给予每个粒子不同的权重,使用加权平均的方法来计算期望 E p ( x ) [ f ( x ) ] = ∫ a b f ( x ) p ( x ) q ( x ) d x = E q ( x ) [ f ( x ) p ( x ) q ( x ) ] E_{p(x)}[f(x)]=\int_a^bf(x)\frac{p(x)}{q(x)}dx=E_{q(x)}[f(x)\frac{p(x)}{q(x)}] Ep(x)[f(x)]=∫abf(x)q(x)p(x)dx=Eq(x)[f(x)q(x)p(x)]我们从提议分布 q ( x ) q(x) q(x)中采样大量粒子 x 1 , x 2 , ⋯ , x n x_1,x_2,\cdots,x_n x1,x2,⋯,xn,每个粒子的权重是 p ( x i ) q ( x i ) \frac{p(x_i)}{q(x_i)} q(xi)p(xi),通过加权平均的方式可以计算出期望 E p ( x ) [ f ( x ) ] = 1 N ∑ f ( x i ) p ( x i ) q ( x i ) E_{p(x)}[f(x)]=\frac{1}{N}\sum f(x_i)\frac{p(x_i)}{q(x_i)} Ep(x)[f(x)]=N1∑f(xi)q(xi)p(xi)
3.1.3、总结
蒙特卡洛方法是一种近似推断的方法,通过采样大量粒子的方法来求解期望、均值、面积、积分等问题,蒙特卡洛对某一种分布的采样方法有直接采样、接受拒绝采样与重要性采样三种,直接采样最简单,但是需要已知累积分布的形式。接受拒绝采样与重要性采样适用于原分布未知的情况,这两种方法都是给出一个提议分布,不同的是接受拒绝采样对不满足原分布的粒子予以拒绝,而重要性采样则是给予每个粒子不同的权重,大家可以根据不同的场景使用这三种方法中的一种进行采样。
3.2、初窥SGVI
首先明确一下我们的目标函数:
q ∗ ( z ) = arg max q ( z ) ∈ Q L ( q ( z ) ) (6) q^*(z)=\arg\max_{q(z)\in Q}L(q(z))\tag{6} q∗(z)=argq(z)∈QmaxL(q(z))(6)我们假设 q ( z ) q(z) q(z)服从某种分布,对应的参数为 ϕ \phi ϕ,则将目标由求解最佳分布 q ∗ ( z ) q^*(z) q∗(z)转化为求最佳分布 q ∗ ( z ) q^*(z) q∗(z)所对应的参数 ϕ \phi ϕ,如果我们能够顺利求出 L ( q ( z ) ) L(q(z)) L(q(z))的梯度,那么采用(7)所示的梯度上升法,我们就通过迭代求得参数的局部最优值:
ϕ t + 1 ← ϕ t + λ ∇ ϕ L ( ϕ ) (7) \phi^{t+1}\gets\phi^t+\lambda\nabla_{\phi}L(\phi)\tag{7} ϕt+1←ϕt+λ∇ϕL(ϕ)(7)下面我们试着推导一下 ∇ ϕ L ( ϕ ) \nabla_{\phi}L(\phi) ∇ϕL(ϕ):
∇ ϕ L ( ϕ ) = ∇ ϕ E q ϕ ( z ) [ log p ( x , z ) − log q ϕ ( z ) ] = ∇ ϕ ∫ z q ϕ ( z ) ( log p ( x , z ) − log q ϕ ( z ) ) d z = ∫ z ∇ ϕ [ q ϕ ( z ) ( log p ( x , z ) − log q ϕ ( z ) ) ] d z ( 交 换 求 导 和 积 分 的 次 序 ) = ∫ z ( ∇ ϕ q ϕ ( z ) ) ( log p ( x , z ) − log q ϕ ( z ) ) d z + ∫ z q ϕ ( z ) ∇ ϕ [ ( log p ( x , z ) − log q ϕ ( z ) ) ] d z ( 乘 法 求 导 法 则 ) = ∫ z ( ∇ ϕ q ϕ ( z ) ) ( log p ( x , z ) − log q ϕ ( z ) ) d z − ∫ z q ϕ ( z ) 1 q ϕ ( z ) ( ∇ ϕ q ϕ ( z ) ) d z = ∫ z ( ∇ ϕ q ϕ ( z ) ) ( log p ( x , z ) − log q ϕ ( z ) ) d z − ∇ ϕ ∫ z ( q ϕ ( z ) ) d z ⏟ = 1 = ∫ z ( ∇ ϕ q ϕ ( z ) ) ( log p ( x , z ) − log q ϕ ( z ) ) d z = ∫ z q ϕ ( z ) ( ∇ ϕ log q ϕ ( z ) ) ( log p ( x , z ) − log q ϕ ( z ) ) d z ( 以 便 写 成 期 望 的 形 式 , 进 而 利 用 蒙 特 卡 洛 采 样 ) = E q ϕ ( z ) [ ( ∇ ϕ log q ϕ ( z ) ) ( log p ( x , z ) − log q ϕ ( z ) ) ] \begin{aligned}\nabla_{\phi}L(\phi)&=\nabla_{\phi}E_{q_{\phi}(z)}[\log p(x,z)-\log q_{\phi}(z)]\\&=\nabla_{\phi}\int_zq_{\phi}(z)(\log p(x,z)-\log q_{\phi}(z))dz\\&=\int_z\nabla_{\phi}[q_{\phi}(z)(\log p(x,z)-\log q_{\phi}(z))]dz(交换求导和积分的次序)\\&=\int_z(\nabla_{\phi}q_{\phi}(z))(\log p(x,z)-\log q_{\phi}(z))dz+\int_zq_{\phi}(z)\nabla_{\phi}[(\log p(x,z)-\log q_{\phi}(z))]dz(乘法求导法则)\\&=\int_z(\nabla_{\phi}q_{\phi}(z))(\log p(x,z)-\log q_{\phi}(z))dz-\int_zq_{\phi}(z)\frac{1}{q_{\phi}(z)}(\nabla_{\phi}q_{\phi}(z))dz\\&=\int_z(\nabla_{\phi}q_{\phi}(z))(\log p(x,z)-\log q_{\phi}(z))dz-\nabla_{\phi}\underbrace{\int_z(q_{\phi}(z))dz}_{=1}\\&=\int_z(\nabla_{\phi}q_{\phi}(z))(\log p(x,z)-\log q_{\phi}(z))dz\\&=\int_zq_{\phi}(z)(\nabla_{\phi}\log q_{\phi}(z))(\log p(x,z)-\log q_{\phi}(z))dz(以便写成期望的形式,进而利用蒙特卡洛采样)\\&=E_{q_{\phi}(z)}[(\nabla_{\phi}\log q_{\phi}(z))(\log p(x,z)-\log q_{\phi}(z))]\end{aligned} ∇ϕL(ϕ)=∇ϕEqϕ(z)[logp(x,z)−logqϕ(z)]=∇ϕ∫zqϕ(z)(logp(x,z)−logqϕ(z))dz=∫z∇ϕ[qϕ(z)(logp(x,z)−logqϕ(z))]dz(交换求导和积分的次序)=∫z(∇ϕqϕ(z))(logp(x,z)−logqϕ(z))dz+∫zqϕ(z)∇ϕ[(logp(x,z)−logqϕ(z))]dz(乘法求导法则)=∫z(∇ϕqϕ(z))(logp(x,z)−logqϕ(z))dz−∫zqϕ(z)qϕ(z)1(∇ϕqϕ(z))dz=∫z(∇ϕqϕ(z))(logp(x,z)−logqϕ(z))dz−∇ϕ=1 ∫z(qϕ(z))dz=∫z(∇ϕqϕ(z))(logp(x,z)−logqϕ(z))dz=∫zqϕ(z)(∇ϕlogqϕ(z))(logp(x,z)−logqϕ(z))dz(以便写成期望的形式,进而利用蒙特卡洛采样)=Eqϕ(z)[(∇ϕlogqϕ(z))(logp(x,z)−logqϕ(z))]至此,我们可以通过蒙特卡洛采样的方法来近似求得梯度,进而利用随机梯度下降来优化参数:
采 样 : z l ∼ q ϕ ( z ) 采样:z^l\sim q_{\phi}(z) 采样:zl∼qϕ(z) 计 算 梯 度 : ∇ ϕ L ( ϕ ) = E q ϕ ( z ) [ ( ∇ ϕ log q ϕ ( z ) ) ( log p ( x , z ) − log q ϕ ( z ) ) ] = 1 L ∑ l = 1 L ( ∇ ϕ log q ϕ ( z ) ) ( log p ( x , z ) − log q ϕ ( z ) ) 计算梯度:\begin{aligned}\nabla_{\phi}L(\phi)&=E_{q_{\phi}(z)}[(\nabla_{\phi}\log q_{\phi}(z))(\log p(x,z)-\log q_{\phi}(z))]\\&=\frac{1}{L}\sum_{l=1}^L(\nabla_{\phi}\log q_{\phi}(z))(\log p(x,z)-\log q_{\phi}(z))\end{aligned} 计算梯度:∇ϕL(ϕ)=Eqϕ(z)[(∇ϕlogqϕ(z))(logp(x,z)−logqϕ(z))]=L1l=1∑L(∇ϕlogqϕ(z))(logp(x,z)−logqϕ(z)) 参 数 更 新 : ϕ t + 1 ← ϕ t + λ ∇ ϕ L ( ϕ ) 参数更新:\phi^{t+1}\gets\phi^t+\lambda\nabla_{\phi}L(\phi) 参数更新:ϕt+1←ϕt+λ∇ϕL(ϕ)但是上述的这个方法其实还是有点问题,由于 q ϕ ( z ) q_{\phi}(z) qϕ(z)是一个概率分布,对其取对数的结果波动非常大,造成直接采样的方差很大。
3.3、重参数化方法解决高方差问题
针对上述的high variance问题,我们可以采用重参数化技巧(Reparameterization)来解决:
在 ∇ ϕ L ( ϕ ) = ∇ ϕ E q ϕ ( z ) [ log p ( x , z ) − log q ϕ ( z ) ] \nabla_{\phi}L(\phi)=\nabla_{\phi}E_{q_{\phi}(z)}[\log p(x,z)-\log q_{\phi}(z)] ∇ϕL(ϕ)=∇ϕEqϕ(z)[logp(x,z)−logqϕ(z)]中,倘若我们能把 E q ϕ ( z ) E_{q_{\phi}(z)} Eqϕ(z)中的 q ϕ ( z ) q_{\phi}(z) qϕ(z)转化成与 ϕ \phi ϕ无关的分布,则我们可以直接对函数 log p ( x , z ) − log q ϕ ( z ) \log p(x,z)-\log q_{\phi}(z) logp(x,z)−logqϕ(z)求导,而不用对它的期望求导,大大降低了复杂度。
原本, z ∼ q ϕ ( z ) z\sim q_{\phi}(z) z∼qϕ(z)。现在我们假设 z = g ϕ ( ϵ , x ) , ϵ ∼ p ( ϵ ) z=g_{\phi}(\epsilon,x),\epsilon\sim p(\epsilon) z=gϕ(ϵ,x),ϵ∼p(ϵ),因此有: ∣ q ϕ ( z ) d z ∣ = ∣ p ( ϵ ) d ϵ ∣ |q_{\phi}(z)dz|=|p(\epsilon)d\epsilon| ∣qϕ(z)dz∣=∣p(ϵ)dϵ∣则求导过程变为: ∇ ϕ L ( ϕ ) = ∇ ϕ E q ϕ ( z ) [ log p ( x , z ) − log q ϕ ( z ) ] = ∇ ϕ ∫ z q ϕ ( z ) ( log p ( x , z ) − log q ϕ ( z ) ) d z = ∫ z ∇ ϕ ( log p ( x , z ) − log q ϕ ( z ) ) q ϕ ( z ) d z = ∫ z ∇ ϕ ( log p ( x , z ) − log q ϕ ( z ) ) p ( ϵ ) d ϵ = E p ( ϵ ) [ ∇ ϕ ( log p ( x , z ) − log q ϕ ( z ) ) ] = E p ( ϵ ) [ ∇ z ( log p ( x , z ) − log q ϕ ( z ) ) ∇ ϕ ( z ) ] ( 链 式 法 则 ) = E p ( ϵ ) [ ∇ z [ ( log p ( x , z ) − log q ϕ ( z ) ] ∇ ϕ g ϕ ( ϵ , x ) ] \begin{aligned}\nabla_{\phi}L(\phi)&=\nabla_{\phi}E_{q_{\phi}(z)}[\log p(x,z)-\log q_{\phi}(z)]\\&=\nabla_{\phi}\int_zq_{\phi}(z)(\log p(x,z)-\log q_{\phi}(z))dz\\&=\int_z\nabla_{\phi}(\log p(x,z)-\log q_{\phi}(z))q_{\phi}(z)dz\\&=\int_z\nabla_{\phi}(\log p(x,z)-\log q_{\phi}(z))p(\epsilon)d\epsilon\\&=E_{p(\epsilon)}[\nabla_{\phi}(\log p(x,z)-\log q_{\phi}(z))]\\&=E_{p(\epsilon)}[\nabla_{z}(\log p(x,z)-\log q_{\phi}(z))\nabla_{\phi}(z)](链式法则)\\&=E_{p(\epsilon)}[\nabla_{z}[(\log p(x,z)-\log q_{\phi}(z)]\nabla_{\phi}g_{\phi}(\epsilon,x)]\end{aligned} ∇ϕL(ϕ)=∇ϕEqϕ(z)[logp(x,z)−logqϕ(z)]=∇ϕ∫zqϕ(z)(logp(x,z)−logqϕ(z))dz=∫z∇ϕ(logp(x,z)−logqϕ(z))qϕ(z)dz=∫z∇ϕ(logp(x,z)−logqϕ(z))p(ϵ)dϵ=Ep(ϵ)[∇ϕ(logp(x,z)−logqϕ(z))]=Ep(ϵ)[∇z(logp(x,z)−logqϕ(z))∇ϕ(z)](链式法则)=Ep(ϵ)[∇z[(logp(x,z)−logqϕ(z)]∇ϕgϕ(ϵ,x)]至此,我们终于完成了基于梯度的变分推断,每次迭代时,我们通过蒙特卡洛采样的方法来近似求得梯度,进而利用随机梯度下降来优化参数: 采 样 : ϵ ∼ p ( ϵ ) 采样:\epsilon\sim p(\epsilon) 采样:ϵ∼p(ϵ) 计 算 z : z = g ϕ ( ϵ , x ) 计算z:z=g_{\phi}(\epsilon,x) 计算z:z=gϕ(ϵ,x) 计 算 梯 度 : ∇ ϕ L ( ϕ ) = E p ( ϵ ) [ ∇ z [ ( log p ( x , z ) − log q ϕ ( z ) ] ∇ ϕ g ϕ ( ϵ , x ) ] 计算梯度:\nabla_{\phi}L(\phi)=E_{p(\epsilon)}[\nabla_{z}[(\log p(x,z)-\log q_{\phi}(z)]\nabla_{\phi}g_{\phi}(\epsilon,x)] 计算梯度:∇ϕL(ϕ)=Ep(ϵ)[∇z[(logp(x,z)−logqϕ(z)]∇ϕgϕ(ϵ,x)] 参 数 更 新 : ϕ t + 1 ← ϕ t + λ ∇ ϕ L ( ϕ ) 参数更新:\phi^{t+1}\gets\phi^t+\lambda\nabla_{\phi}L(\phi) 参数更新:ϕt+1←ϕt+λ∇ϕL(ϕ)