一、时间复杂度
1 常见的时间复杂度
- #常量阶O(1)
- # 对数阶O(logn)
- # 线性对数阶O(nlogn)
- # 线性阶O(n)
- # 平方阶,立方阶....M次方阶O(n^2),O(n^3),O(n^m)
- # 指数阶O(2^n)
- # 阶乘阶O(n!)
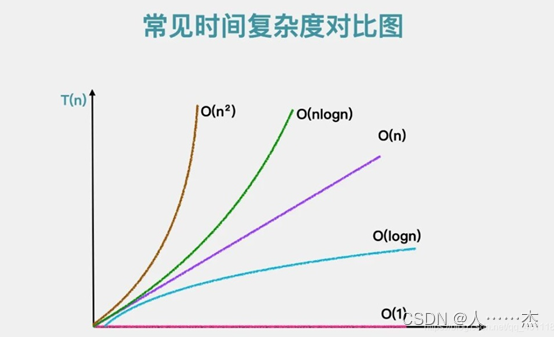
算法的时间复杂度对比:
O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n2logn)<O(n3)
其中,算法的时间复杂度越低,算法的效率越高。
2 时间复杂度的计算过程中的忽略原则
- 加法常数项可以忽略
- 除去最高阶项,其它次项可以忽略
- 与最高次项相乘的常数可以忽略
3 大O计法
表示方法:T(n)=O(f(n))
该公式中的O表示代码的执行总时间T(n)和其执行总次数f(n)成正比。这种表示法,称之为大O记法。大O记法T(n)=O(f(n)),表示随着代码执行的次数增长(减少),算法执行时间的增长率和f(n)的增长率相同,表示的是算法的渐近时间复杂度,简称时间复杂度。
二、时间复杂度分析案例
1 常量阶O(1)
1.1 案例1
# 常数阶1
num = 1 # 只执行一次
num = num + n # 只执行一次
print(num) # 只执行一次
分析:
f(n)是指算法中所有语句的执行次数,这里便是f(n)=3,时间复杂度为O(f(n)),所以应该为O(3),可是为什么用O(1)表示呢?这里就是大O表示的法第一条即“用常数1等价替代不受数据规模影响的基本操作”。
2 对数阶O(logn)
2.1 案例1
# 对数阶1
i = 1
while i <= n: i = i * 2
分析:

所以求出x的值,就知道执行多少次了 ,也就是2的x次幂=n,x=log2n就是时间复杂度。显然就是O(log2n)。而所有对数的时间复杂度都表示为O(logn), 因为log2n=log3n/log32=log23*log3n,根据忽略原则中的“与最高次项相乘的常数可以忽略”,则可以表示为log2n=log3n,而当n为无穷大的时候,底数是2或者3都没有什么意义,所以统一表示为logn。
根据乘法法则,如果一段代码的时间复杂度为O(logn),循环执行n遍,时间复杂度就是O(nlogn),即线性对数阶。O(nlogn)也是非常常见的时间复杂度,如归并排序,快速排序。
对数公式:

2.2 案例2
# 对数阶2
n = 8
count = 0
while n>1:n = n//2count += 1
print('程序共被执行了:',count,'次')
分析:
程序一共被执行了3次,也是x=log2n,即时间复杂度为 O(logn)。
3 线性对数阶O(nlogn)
# 线性对数阶
for j in range(n):i = 1while i <= n:i *= 2
4 线性阶O(n)
4.1 案例1
sum = 0 # 只执行一次
for i in range(0, n): # 执行n次count = count + 1 # 执行n次
分析:
上面代码执行的总次数为:f(n) = 1 + n + n;所以时间复杂度为T1(n) = O(2*n + 1)。当n趋近于无穷大时,T1(n) = O(n);
4.2 案例2
# 线性阶举例2
count = 0 # 只执行一次
sum = 0 # 只执行一次for i in range(0, n): # 执行n次count = count + 1 # 执行n次for j in range(0, n): # 执行n次sum += j # 执行n次sum += 2*j # 执行n次
分析:
增加前(即4.1)时间复杂度为:T1(n) = O(2n + 1),增加部分的代码执行次数f(n) = 1 + n + n + n;所以增加的代码时间复杂度T2(n) = O(3n + 1);因为代码是平行增加的所以增加后的时间复杂度T(n) = T1(n) + T2(n) = O(5*n + 2)。当n趋近于无穷大时,T(n) = O(n);
加法法则:如果算法的代码是平行增加的,则只需加上所对应的时间复杂度。
可以总结为:设T1(n)=O(f(n)),T2(n)=O(g(n)),则 T1(n)+T2(n)=O(max(f(n), g(n)))
5 平方阶O(n^2)
5.1 案例1
#平方阶举例1
n = 5
sum = 0 # 执行一次
for i in range(0, n): # 执行n次b = 2 * i # 执行n次for j in range(0, n): # 执行n*n次sum += i + j # 执行n*n次
分析:
分析得出上面代码执行的总次数f(n) = 1 + n + n + nn + nn = 2n²+2n+1 。因此可以推出时间复杂度T(n) = O(2n²+2n+1 )。当n趋近于无穷大时,T(n)的增长主要与n²有关系,所以我们通常也将上述代码的时间复杂度写为T(n) = O(n²);
5.2 案例2
#平方阶举例2
sum = 0 # 只执行一次
for i in range(0, n): # 执行n次count = count + 1 # 执行n次for j in range(0, m): # 执行n*m次count = count + 1 # 执行n*m次
分析:
上面代码在4.1上增加了一个内层循环,增加的部分如果单独看,则执行了m次,但是由于是嵌套增加的,所以当外层循坏执行一次,内层循环就会执行m次。所以当外层循环执行n次时,内层循环就会执行n*m次,所以下面代码执行的总次数f(n) = 1 + n + n + nm + nm。由时间复杂度O的定义可计算出下面代码的时间复杂度T(n) = O(2nm + 2n + 1)。当n和m趋近于无穷大时,可以认为n=m,则可以写为T(n) = O(2n² + 2n + 1)。由于n和m趋近于无穷大,所以T(n)的增长主要受n²的增长影响,所以可以写为T(n) = O(n²)
乘法法则:如果算法的代码增加的是循环内的嵌套或者函数的嵌套,那么就需要乘上相应的时间复杂度。
可以总结为:设T1(n)=O(f(n)),T2(n)=O(g(n)),则 T1T2=O(f(n)g(n))
6 立方阶O(n^3)
6.1 案例1
n = 5
count = 0
for i in range(n):for j in range(n):for k in range(n):count += 1
print('程序共被执行了:',count,'次')
6.2 案例2
# 指数阶 递归
n = 6
def fib(n):if n<2:return nreturn fib(n-1)+fib(n-2)
print('斐波拉契',n,'为:',fib(n))
分析:
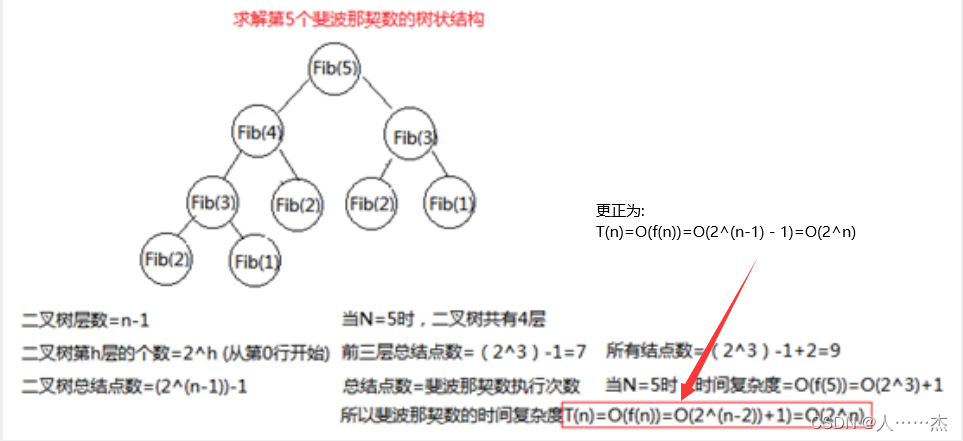
三、练习题
1 设n是描述问题规模的非负整数,下面程序片段的时间复杂度是()。
x = 2
while x < n/2 :x = 2*xprint(x)
A. O(log2n) B. O(n) C. O(nlog2n) D. O(n2)
分析:
在程序中,执行频率最高的语句为“x=2*x”。设该语句共执行了 t次,则2t+1=n/2,故t=log2(n/2)-1=log2n-2,得 T(n)=O(log2n)。故选A.
2 求整数n (n>=0)阶乘的算法如下,其时间复杂度是( )。
# 习题2
def fact(n):if n<=1:return 1return n*fact(n-1)
A. O(log2n) B. O(n) C. O(nlog2n) D. O(n2)
分析:
本题是求阶乘n!的递归代码,即n*(n-1)*...*1共执行n次乘法操作,故T(n)=O(n)。
3 计算下面的时间复杂度:
# 习题3
i = 1
while i <= n:i = i * 3
分析:
即为O(log3n),所有对数的时间复杂度都为O(logn)。
四、参考
1.https://blog.csdn.net/weixin_40006977/article/details/110548314
2.Python常用算法之时间复杂度_假书生@的博客-CSDN博客_python 时间复杂度
3.
时间复杂度和空间复杂度(Python)_狂奔的菜鸡的博客-CSDN博客_时间复杂度python
4.「Python语言进阶」算法复杂度是什么?如何估算?
5.数据结构与算法分析——对数时间复杂度的算法_ikilig404的博客-CSDN博客_对数运算时间复杂度
6.
数据结构与算法 --时间复杂度分析(二)_star_chao的博客-CSDN博客
7.数据结构(二)——时间复杂度+例子分析(相当清晰)_程序猿成长轨迹的博客-CSDN博客_数据结构时间复杂度例子
8.
数据结构——时间复杂度_ZJH_12138的博客-CSDN博客_数据结构时间复杂度