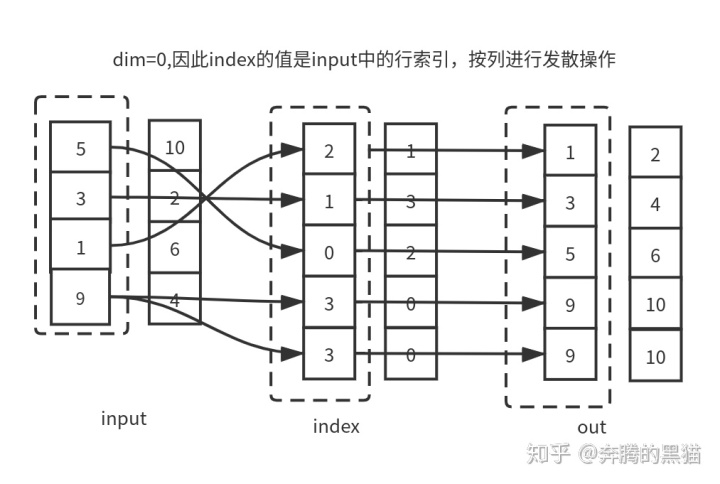
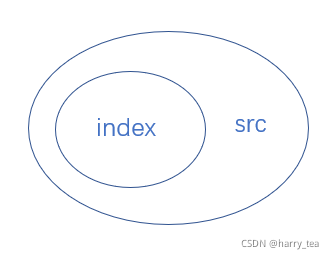
在 算法基础 中，我们简单介绍了什么是算法、对算法的要求，以及说了评断算法效率的两大类方法。今天我们将重点介绍衡量算法效率的一个概念——时间复杂度。

---

定义

在进行算法分析的时候，语句的总执行次数 T(n) 是关于问题规模 n（输入数据量）的函数，换句话说：代码总的执行时间 T(n) 和每行代码执行的次数 n 成正比。一般记做 T(n)=O(f(n))。其中用大写 O() 来体现时间复杂度的记法，我们称之为大 O 记法。

大 O 时间复杂度实际上并不具体表示代码真正的执行时间，而是表示代码执行时间随数据规模增长的变化趋势，所以，也叫作渐进时间复杂度（asymptotic time complexity），简称时间复杂度。

那什么情况下，算法的时间复杂度才好呢？当然是「多个算法中，随着 n 的增大，T(n) 增长最慢」的算法才是好算法呀。

既然说到了「慢」，怎样就增长得慢了呢？想想咱们说一个人跑得快，是不是就是说他跑的速率低呀，那类比过来，无疑是增长率（增量/原总量*100%）比较低的增长得慢了呗。

大 O 记法

常见时间复杂度

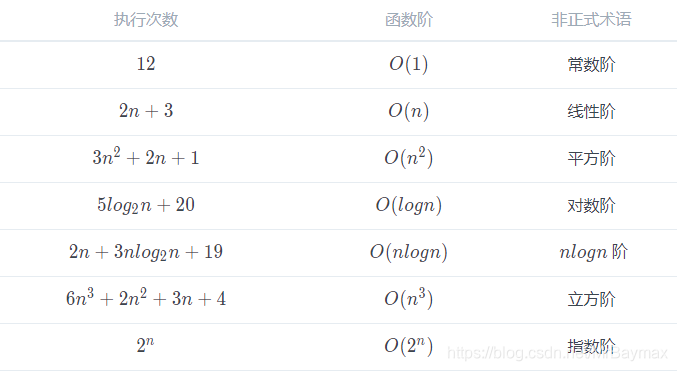
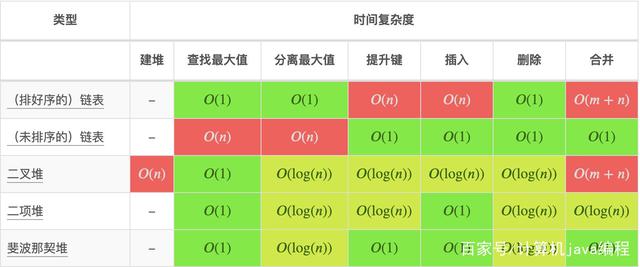
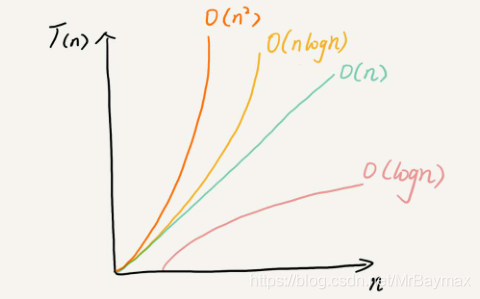
常用的时间复杂度所耗费的时间从少到多依次是：

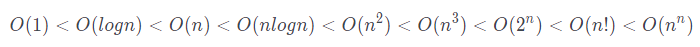
再贴一个盗来的图吧：

大 O 阶方法的推导

1. 用常数 1 取代运行时间中的所有加法常数。
2. 在修改后的运行次数函数中，只保留最高阶项。
3. 如果最高阶项存在且不是1，则去除与这个项相乘的常数。

得到的结果就是大O阶。

常见时间复杂度实例分析

推导时间复杂度的时候，上述的「大 O 阶方法的推导」一定要用上，再分享下自己常用的几个法则：

• 法则一：只关注循环执行次数最多的一段代码
• 法则二：加法法则->总复杂度等于量级最大的那段代码的复杂度
• 法则三：乘法法则->嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

常数阶

与问题的大小（n 的大小）无关，执行时间恒定的算法，称之为具有 O(1) 的时间复杂度，又叫常数阶。

不管常数是多少，都记作 O(1) ，而不是 O(2)、O(4) 等其它数字。

另外，对于单纯的分支结构（不在循环内）来说，不管真假执行的次数都是恒定的，不会随 n 的大小变化。

线性阶

比如看下面的代码：

int i;
for (i = 0; i < n; i++){    // 时间复杂度为 O(1) 的程序步骤序列
}

循环结构的代码比单纯的分支结构代码或者只执行固定次数的代码复杂一些。咱们要确定时间复杂度的话，需要确定某个语句（集）执行的次数。

这个时候法则一和三就登场了：最外层循环执行 n 次，循环体中的执行都是 1 次，n*1=n，显而易见上述代码的时间复杂度为 O(n)。

对数阶

看下面代码：

int count = 1;
while (count < n){// 时间复杂度为 O(1) 的程序步骤序列count = count * 2;
}

根据法则一，咱们只关注循环执行次数最多的一段代码，这个循环执行多少次呢？是不是会有这个式子 $2^x$=n，算出来 x 是不是 x=${\log }_{2}n$；然后再利用法则三，是不是可以算出来上述代码的时间复杂度为 ${\log }_{2}n$ 了。

如果代码中的 count = count * 2; 是 count = count * 3; 呢，是不是就不用说了。

平方阶

下面的代码是个双层 for 循环：

int i, j;
for (i = 0; i < n; i++){    for (j = 0; j < n; j++){        // 时间复杂度为 O(1) 的程序步骤序列 }
}

内循环的时间复杂度是 O(n)，咱们已经分析过了。外层的循环次数也是 n 次，法则三直接可以得出上述代码的时间复杂度为 O($n^2$)。

如果上述代码是下面的样子呢：

int i, j;
for (i = 0; i < m; i++){    for (j = 0; j < n; j++){        // 时间复杂度为 O(1) 的程序步骤序列 }
}

没错，就是 O($mn$)。

再来个有难度的例子：

int i, j;
for (i = 0; i < n; i++){   // 注意现在是 j=i，而不是 j=0for (j = i; j < n; j++){        // 时间复杂度为 O(1) 的程序步骤序列    }
}

上述代码的时间复杂度是多少呢？简单分析下：

• 当 i=0 时，内循环执行 n 次；
• 当 i=1 时，内循环执行了 n-1 次；
• ……；
• 当 i=n-1 时，执行 1 次；
• 总的执行次数为 $n+(n-1)+(n-2)+\dots +1$$=$$\frac{n(n+1)}{2}$$=$$\frac{n^2}{2}$+$\frac{n}{2}$。

此时，就到大 O 阶方法的推导发挥的时候了：

1. 第一条，没有加法常数，不考虑；
2. 第二条，保留最高项，得到 $\frac{n^2}{2}$；
3. 第三条去除最高项的常数，也就是 $\frac{1}{2}$，得到时间复杂度为 O($n^2$)。

其他名词

先来一段代码吧：

// n 表示数组 array 的长度
int find(int[] array, int n, int x) {int i = 0;int position = -1;for (; i < n; ++i) {if (array[i] == x){position = i;}}return position;
}

上述代码的功能是在一个无序数组中，查找变量 x 出现的位置，如果没找到，则返回 -1。由上面说到的分析方法，不难知道代码的时间复杂度为 O($n$)。

下面我们来做下优化，如果我们在数组中查找某个元素，是并不需要把数组中的所有元素遍历一遍的，因为中途可能就发现答案，然后就可以提前结束循环了。下面的代码是优化过的，这个时候时间复杂度就不为 O($n$) 了。

// n 表示数组 array 的长度
int find(int[] array, int n, int x) {int i = 0;int position = -1;for (; i < n; ++i) {if (array[i] == x){position= i;break;}}return position;
}

针对上述代码，咱们分三种情况讨论：

• 情况一：数组中的第一个元素就是待查找元素，时间复杂度为 O($1$)；
• 情况二：数组中的最后一个元素是待查找元素，时间复杂度为 O($n$)；
• 情况三：在数组中的不确定的位置，位置有 n+1 种情况（在数组中，不在数组中），我们把每种情况下的需要遍历的元素个数加起来，然后除 n+1，得到需要遍历元素的评价值：即$\frac{1+2+3+\dots \dots +n+n}{n+1}$=$\frac{n(n+3)}{2(n+1)}$，然后再根据上文说到的计算时间复杂度的规则，得到平均时间复杂度为 O($n$)。

情况三中涉及到概率问题，具体的看图吧（重点已经标注）：

这次再引入下面三个名词应该就好点了吧：

1. 最好情况时间复杂度：在最理想的情况下，执行这段代码的时间复杂度。

2. 最坏情况时间复杂度：在最糟糕的情况下，执行这段代码的时间复杂度。

3. 平均情况时间复杂度：看图上的说明即可~

均摊时间复杂度，还是看下极客时间的教程吧：

其实大概意思就是如果对某个数据结构进行一组连续操作的时候，大部分情况下时间复杂度还是很低的，个别比较高，这个时候咱们将这一组操作放一块看，把时间复杂度较高的操作耗时平摊到耗时低的操作上。而且 在能够应用均摊时间复杂度分析的场合，一般均摊时间复杂度就等于最好情况时间复杂度。

这部分内容的话，推荐大家看看 复杂度分析（下）：浅析最好、最坏、平均、均摊时间复杂度。

---

这篇博客虽然不是特别长，但是写出来耗费的时间还挺长；虽也没有生动的例子，还是希望自己一个各位能好好理解并应用了；虽然只是简单介绍了时间复杂度的相关内容，但是还可以看看下篇的 空间复杂度 啊~