一、基本概念

      ANN：Artificial neural network前馈神经网络的缩写

二、模型构建

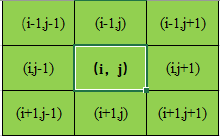
2.1 神经元

      

2.2 激活函数

意义：激活函数是用来让给神经网络加入非线性因素的，因为线性模型的表达能力不够。如果没有激活函数，那么该网络仅能表达线性映射，此时即便有再多的隐藏层，其整个网络跟单层神经网络也是等价的。

激活函数应该如下性质：

1）非线性；

2）连续可微，容易求导，梯度下降法进行参数求解的要求；

3）范围最好不饱和，当有饱和的区间段时，若系统优化进入该阶段，梯度近似为0，网络的学习就会停止；

4）单调性，单调神经网络的误差函数是凸的，容易进行凸优化；

激活函数有哪几种，各自的特点及使用场景？

1）sigmoid

          

        

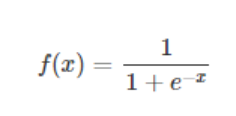
f′(x)=f(x)(1−f(x))

sigmoid也有其自身的缺陷，最明显的就是饱和性，具体来说，由于在后向传播过程中，sigmoid向下传导的梯度包含了一个f'(x)因子，因此一旦输入落入饱和区，f'(x)就会变得接近于0，导致了向底层传递的梯度也变得非常小。此时，网络参数很难得到有效训练和更新。这种现象称为梯度消失。一般来说，sigmoid网络在5层之内就会产生梯度消失现象。

此外，sigmoid函数的输出均大于0，使得输出不是0均值，这称为偏移现象，这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入。

2）tanh

tanh也是一种非常常见的激活函数，与sigmoid相比，它的输出均值是0，使得其收敛速度要比sigmoid快，减少迭代次数。然而，tanh一样具有饱和性，从而造成梯度消失。

3. ReLu

优点：

梯度计算简单，即是非线性函数，又避免了sigmoid的指数计算量大的问题

半饱和

半区域抑制，既有优点(神经网络稀疏性)，又有缺点(神经元死亡），起到了类似于L1的正则化通，可以在一定程度上缓解过拟合。

为什么ReLu比sigmoid好？

1.连乘导致梯度下降；

2.饱和区域：sigmoid是双饱和区，ReLU单侧饱和，而且ReLU的单侧饱和可以实现神经网络的稀疏性，有好处。

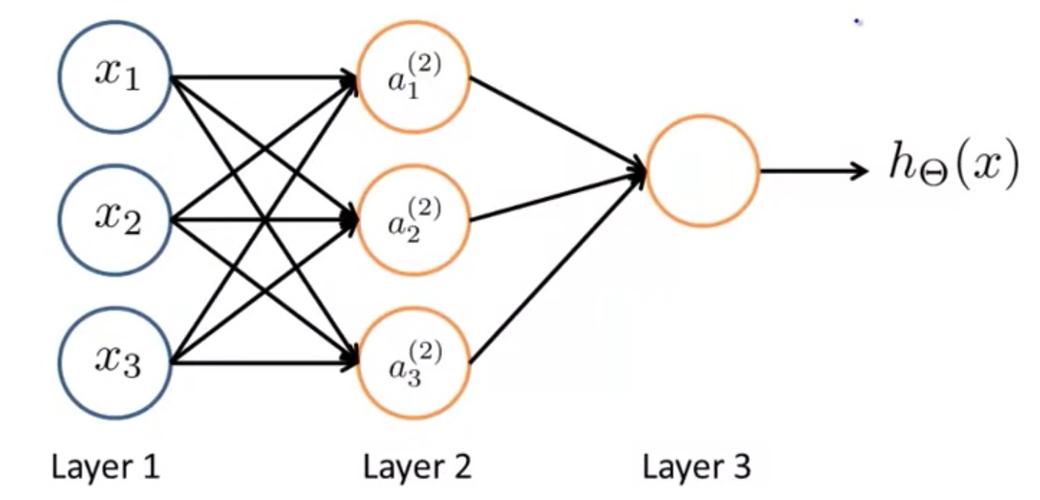
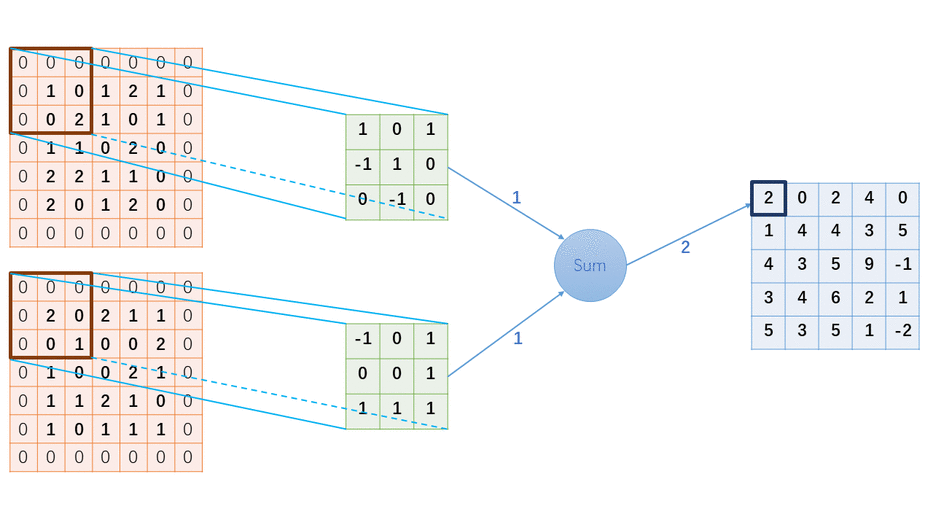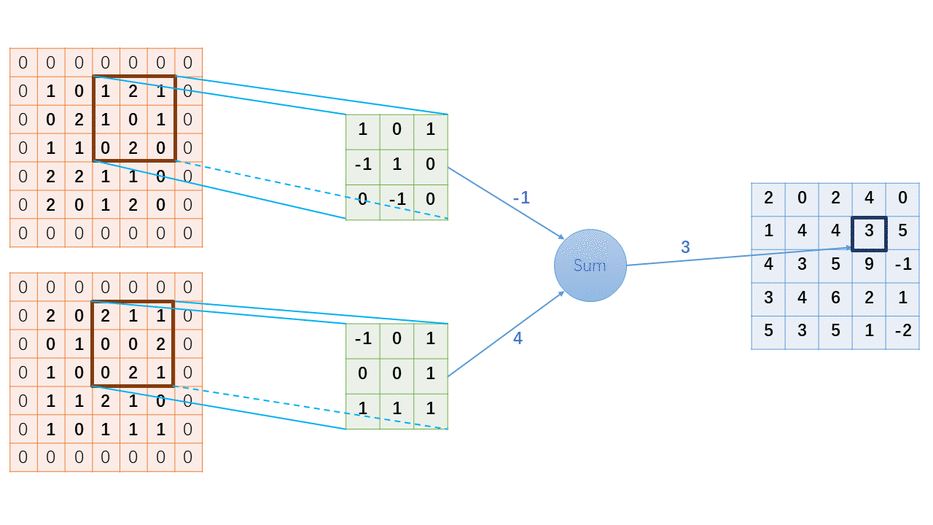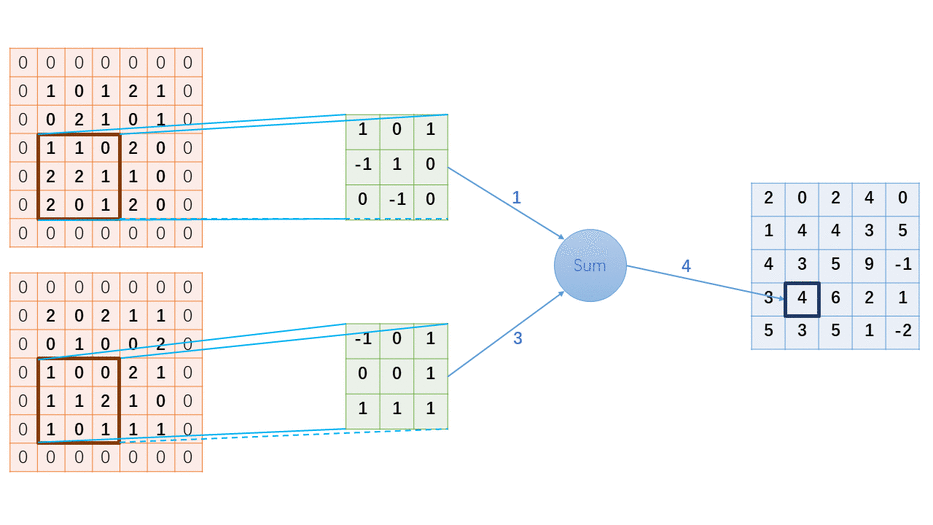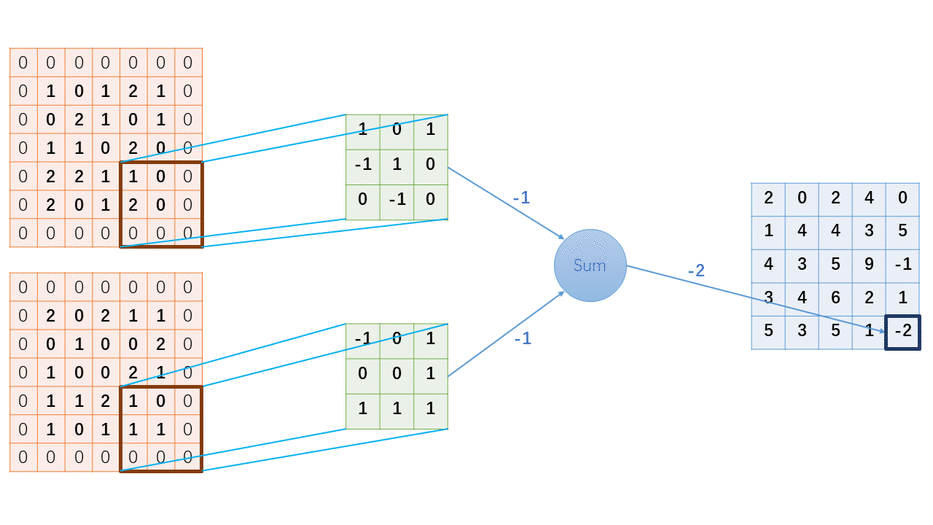
2.3 模型构建图

     

三、损失函数

从神经网络的学习目标来说，如果是要做个分类器的话就是交叉熵损失函数，要做回归问题的话就用MSE.

3.1 交叉熵损失函数

1） softmax

多分类的normailization，它是将神经网络得到的多个值，进行归一化处理，使得到的值在[0,1]之间，让结果变得可解释。即可以将结果看做是概率，某个类别的概率大，将样本归为该类别的可能性也越高。softmax公式如下：

          

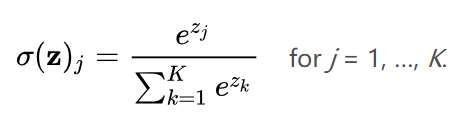
2）交叉熵损失函数

神经网络的多分类问题，先用softmax把概率进行归一化，再采用交叉熵损失函数作为loss function。

3.4 L1和L2正则解决过拟合

3.5 Dropout的过拟合方案

Dropout是指在深度学习网络的训练过程中，对于神经网络单元，按照一定的概率将其暂时从网络中丢弃。注意是暂时。

对于随机梯度下降来说，由于是随机丢弃，故而每个mini-batch都在训练不同的网络。

我们可以把dropout当做一种多模型效果平均的方式。对于减少测试集中的错误，我们可以将多个不同神经网络的预测结果取平均，而因为dropout的随机性，我们每次dropout后，网络模型都可以看成是一个不同结构的神经网络，提升了网络的鲁棒性。

四、模型优化

 4.1 优化方法 — 梯度下降法

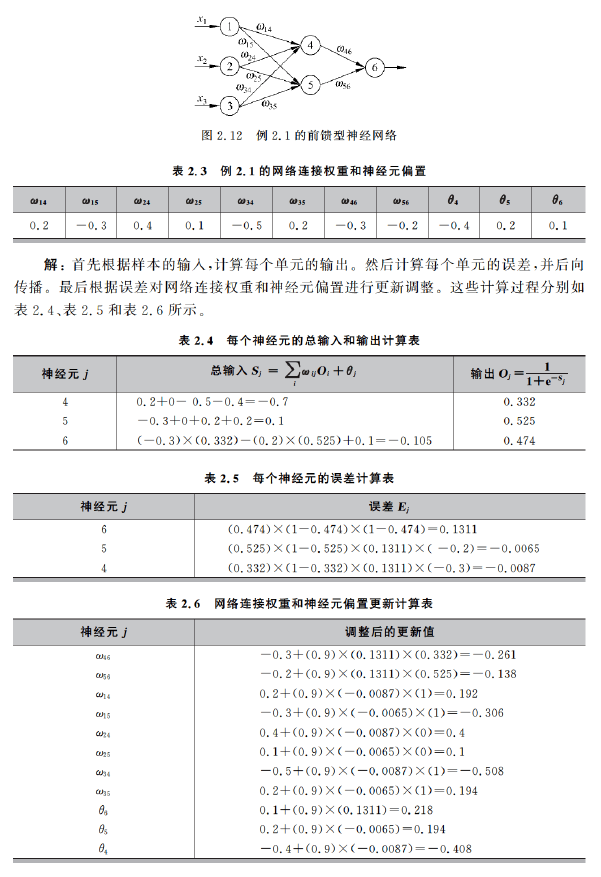
4.2 参数更新，反向传播算法

梯度下降是反复迭代计算loss函数对w，b的偏导。反向传播思想可以用来方便的求出loss函数对每个参数的导数，其基本原理是求导时的链式法则。

BP思想：计算输出与标签见的损失函数值，然后计算其相对于每个神经元的梯度，根据梯度方向更新权值。

（1）将训练集数据输入到ANN的输入层，经过隐藏层，最后达到输出层并输出结果，这是ANN的前向传播过程；

（2）由于ANN的输出结果与实际结果有误差，则计算估计值与实际值之间的差，将该差值从输出层向隐藏层方向传播，直至传播到输入层；

（3）在反向传播的过程中，根据误差调整各种参数的值；不断迭代上述过程，直至收敛。

五、神经网络参数初始化问题