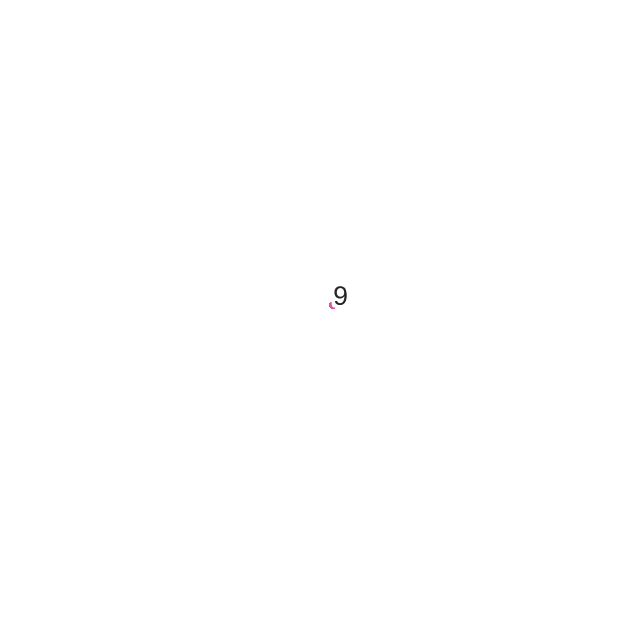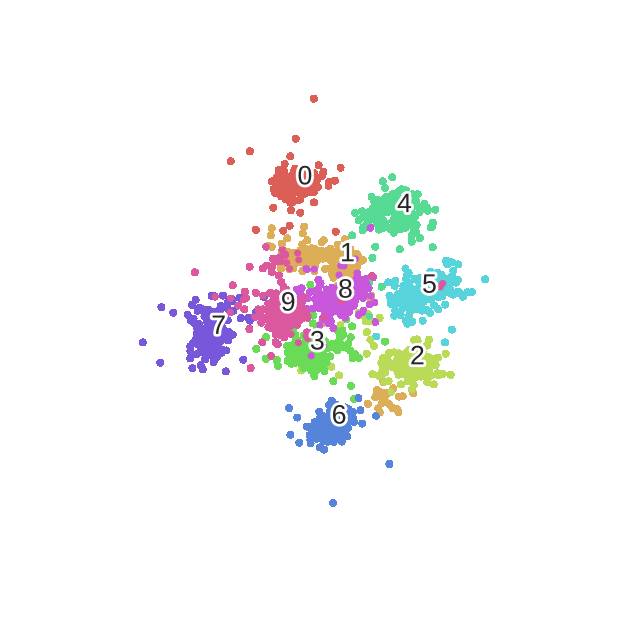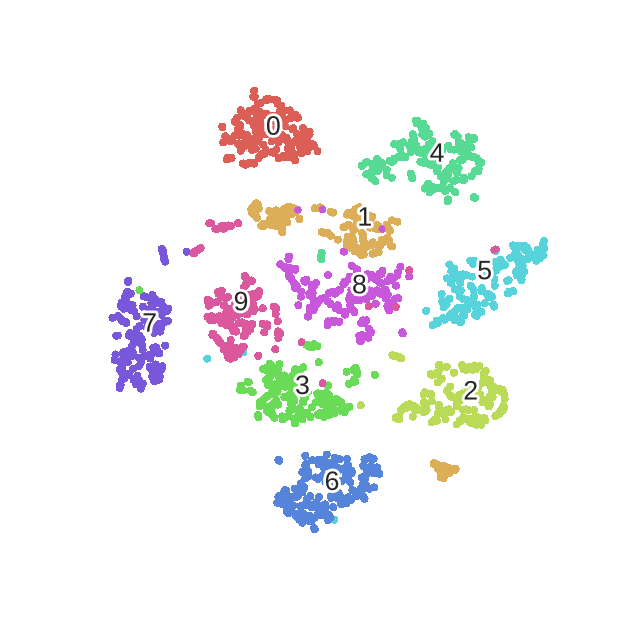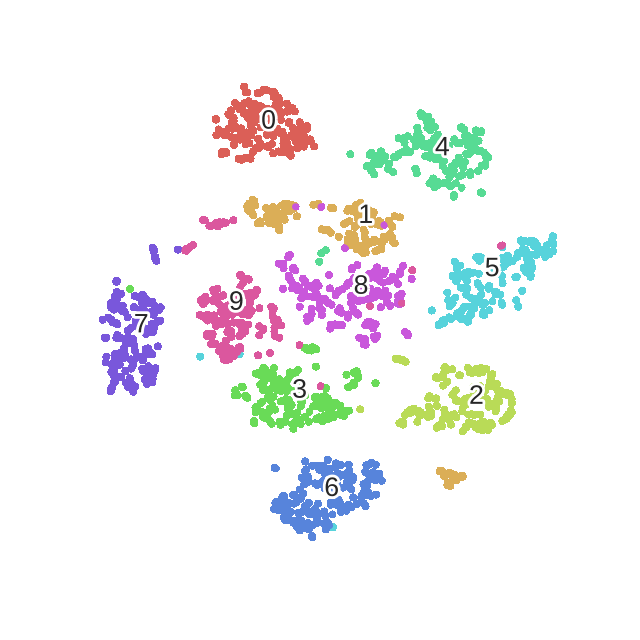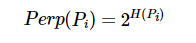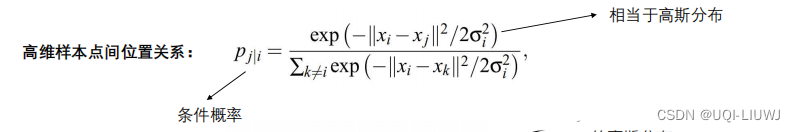SNE
基本原理
SNE是通过仿射变换将数据点映射到概率分布上,主要包括两个步骤:
1) SNE构建一个高维对象之间的概率分布,使得相似的对象有更高的概率被选择,而不相似的对象有较低的概率被选择。
2) SNE在低维空间里在构建这些点的概率分布,使得这两个概率分布之间尽可能的相似。
t-SNE模型是无监督的降维,只能单独的对数据做操作,它只有fit_transform,而没有fit操作。
SNE原理推导
SNE是先将欧几里得距离转换为条件概率来表达点与点之间的相似度。具体来说,给定一个N个高维的数据 x 1 , x 2 , . . . , x N x_1,x_2,...,x_N x1,x2,...,xN(注意N是数据样本数量,不是维度), t-SNE首先是计算概率 p j ∣ i p_{j|i} pj∣i,正比于数据点 x i 与 x j x_i 与 x_j xi与xj之间的相似度(具体的概率密度函数由算法设计人员自主构建),即:
这里的有一个参数是 σ i \sigma_i σi,对于不同的点 x i x_i xi取值不一样,通常取值为以数据点 x i x_i xi为中心的高斯均方差。下文会讨论具体设置。此外设置 p i ∣ i = 0 p_{i|i}=0 pi∣i=0,因为我们关注的是两两之间的相似度。
那对于低维度下的 y i y_i yi,我们可以指定高斯分布的均方差为 1 2 \frac{1}{\sqrt2} 21,因此它们之间的相似度如下:
同样,设定 q i ∣ i = 0 q_{i|i}=0 qi∣i=0。
如果降维的效果比较好,局部特征保留完整,那么 q j ∣ i = p j ∣ i q_{j|i}=p_{j|i} qj∣i=pj∣i 。因此我们优化两个概率分布之间的距离即KL散度 (交叉熵),那么目标函数如下:
这里的 P i P_i Pi表示了给定点 x i x_i xi下,其他所有数据点的条件概率分布。需要注意的是KL散度具有不对称性,在低维映射中不同的距离对应的惩罚权重是不同的,具体来说:距离较远的两个点来表达距离较近的两个点会产生更大的cost,相反,用较近的两个点来表达较远的两个点产生的cost相对较小(注意:类似于回归容易受异常值影响,但效果相反)。即用较小的 q j ∣ i = 0.2 q_{j|i}=0.2 qj∣i=0.2来建模较大的 p j ∣ i = 0.8 p_{j|i}=0.8 pj∣i=0.8, c o s t = p l o g ( p / q ) = 1.11 cost=plog(p/q)=1.11 cost=plog(p/q)=1.11同样用较大的 q j ∣ i = 0.8 q_{j|i}=0.8 qj∣i=0.8来建模较大的 p j ∣ i = 0.2 , c o s t = − 0.277 p_{j|i}=0.2, cost=-0.277 pj∣i=0.2,cost=−0.277因此,SNE会倾向于保留数据中的局部特征。
下面我们开始正式的推导SNE。首先不同的点具有不同的 σ i \sigma_i σi, P i P_i Pi的熵会随着 σ i \sigma_i σi的增加而增加。SNE使用困惑度的概念,用二分搜索的方式来寻找一个最佳的 σ \sigma σ。其中困惑度指:
这里的 H ( P i ) H(P_i) H(Pi) 是 P i P_i Pi的熵,即:
困惑度可以解释为一个点附近的有效近邻点个数。SNE对困惑度的调整比较有鲁棒性,通常选择5-50之间,给定之后,使用二分搜索的方式寻找合适的 σ \sigma σ。
那么核心问题是如何求解梯度了,目标函数等价于 ∑ ∑ − p l o g ( q ) \sum \sum - p log(q) ∑∑−plog(q) 这个式子与softmax非常的类似,我们知道softmax的目标函数是 ∑ − y log p \sum -y \log p ∑−ylogp,对应的梯度是 y − p y - p y−p (注:这里的softmax中y表示label,p表示预估值)。 同样我们可以推导SNE的目标函数中的 i i i 在 j j j下的条件概率情况的梯度是 2 ( p i ∣ j − q i ∣ j ) ( y i − y j ) 2(p_{i \mid j}-q_{i \mid j})(y_i-y_j) 2(pi∣j−qi∣j)(yi−yj), 同样 j j j在 i i i下的条件概率的梯度是 2 ( p j ∣ i − q j ∣ i ) ( y i − y j ) 2(p_{j \mid i}-q_{j \mid i})(y_i-y_j) 2(pj∣i−qj∣i)(yi−yj), 最后得到完整的梯度公式如下:
在初始化中,可以用较小的 σ \sigma σ下的高斯分布来进行初始化。为了加速优化过程和避免陷入局部最优解,梯度中需要使用一个相对较大的动量。即参数更新中除了当前的梯度,还要引入之前的梯度累加的指数衰减项 (可以先使用较大的学习率来快速得到一个比较优的解,然后随着迭代的继续逐步减小学习率,使得模型在训练后期更加稳定),如下:
这里的 Y ( t ) Y^{(t)} Y(t)表示迭代t次的解, η \eta η表示学习速率, α ( t ) \alpha(t) α(t)表示迭代 t t t 次的动量。
此外,在初始优化的阶段,每次迭代中可以引入一些高斯噪声 (它的概率密度函数服从高斯分布(即正态分布)),之后像模拟退火一样逐渐减小该噪声,可以用来避免陷入局部最优解。因此,SNE在选择高斯噪声,以及学习速率,什么时候开始衰减,动量选择等等超参数上,需要跑多次优化才可以。
t-SNE
尽管SNE提供了很好的可视化方法,但是他很难优化,而且存在”crowding problem”(拥挤问题)。后续中,Hinton等人又提出了t-SNE的方法。与SNE不同,主要如下:
使用对称版的SNE,简化梯度公式
低维空间下,使用t分布替代高斯分布表达两点之间的相似度
t-SNE在低维空间下使用更重长尾分布的t分布来避免crowding问题和优化问题。在这里,首先介绍一下对称版的SNE,之后介绍crowding问题,之后再介绍t-SNE。
2.1 Symmetric SNE
优化 p i ∣ j p_{i \mid j} pi∣j 和 q i ∣ j q_{i \mid j} qi∣j 的KL散度的一种替换思路是,使用联合概率分布来替换条件概率分布,即P是高维空间里各个点的联合概率分布,Q是低维空间下的,目标函数为:
这里的 p i ∣ i p_{i \mid i} pi∣i 与 p j ∣ j p_{j \mid j} pj∣j 为 0,我们将这种SNE称之为symmetric SNE(对称SNE),因为他假设了对于任意 i , p i j = p j i , q i j = q j i i,p_{ij} = p_{ji}, q_{ij} = q_{ji} i,pij=pji,qij=qji,因此概率分布可以改写为:
这种表达方式,使得整体简洁了很多。但是会引入异常值的问题。比如 x i x_i xi 是异常值,那么 ∣ ∣ x i − x j ∣ ∣ 2 \mid \mid x_i - x_j \mid \mid ^2 ∣∣xi−xj∣∣2 会很大,对应的所有的 j , p i j j,p_{ij} j,pij 都会很小(之前是仅在 x i x_i xi 下很小),导致低维映射下的 y i y_i yi 对 cost 影响很小。
为了解决这个问题,我们将联合概率分布定义修正为: p i j = p i ∣ j + p j ∣ i 2 p_{ij} = \frac{p_{i \mid j} + p_{j \mid i}}{2} pij=2pi∣j+pj∣i 这保证了 ∑ j p i j > > 1 2 n \sum_j p_{ij} > \gt {}\frac{1}{2n} ∑jpij>>2n1 , 使得每个点对于cost都会有一定的贡献。对称SNE的最大优点是梯度计算变得简单了,如下:
Crowding问题
拥挤问题就是说各个簇聚集在一起,无法区分。比如有一种情况,高维度数据在降维到10维下,可以有很好的表达,但是降维到两维后无法得到可信映射,比如降维如10维中有11个点之间两两等距离的,在二维下就无法得到可信的映射结果(最多3个点)。 进一步的说明,假设一个以数据点 x i x_i xi 为中心,半径为r的m维球(三维空间就是球),其体积是按 r m r_m rm 增长的,假设数据点是在m维球中均匀分布的,我们来看看其他数据点与 x i x_i xi的距离随维度增大而产生的变化。
从上图可以看到,随着维度的增大,大部分数据点都聚集在m维球的表面附近,与点 x i x_i xi的距离分布极不均衡。如果直接将这种距离关系保留到低维,就会出现拥挤问题。
Cook et al.(2007) 提出一种slight repulsion的方式,在基线概率分布(uniform background)中引入一个较小的混合因子 ρ \rho ρ,这样 q i j q_{ij} qij 就永远不会小于 2 ρ n ( n − 1 ) \frac{2 \rho}{n(n-1)} n(n−1)2ρ (因为一共了 n ( n − 1 ) n(n-1) n(n−1)个pairs),这样在高维空间中比较远的两个点之间的 q i j q_{ij} qij 总是会比 p i j p_{ij} pij 大一点。这种称之为UNI-SNE,效果通常比标准的SNE要好。优化UNI-SNE的方法是先让 ρ \rho ρ 为0,使用标准的SNE优化,之后用模拟退火的方法的时候,再慢慢增加 ρ \rho ρ . 直接优化UNI-SNE是不行的(即一开始 ρ \rho ρ 不为0),因为距离较远的两个点基本是一样的 q i j q_{ij} qij (等于基线分布), 即使 p i j p_{ij} pij 很大,一些距离变化很难在 q i j q_{ij} qij 中产生作用。也就是说优化中刚开始距离较远的两个聚类点,后续就无法再把他们拉近了。
t-SNE
对称SNE实际上在高维度下 另外一种减轻”拥挤问题”的方法:在高维空间下,在高维空间下我们使用高斯分布将距离转换为概率分布,在低维空间下,我们使用更加偏重长尾分布的方式来将距离转换为概率分布,使得高维度下中低等的距离在映射后能够有一个较大的距离。
我们对比一下高斯分布和t分布(小样本的正态分布), t分布受异常值影响更小,拟合结果更为合理,较好的捕获了数据的整体特征。
使用了t分布之后的q变化,如下:
此外,t 分布是无限多个高斯分布的叠加,计算上不是指数的,会方便很多。优化的梯度如下:
t-sne的有效性,也可以从上图中看到:横轴表示距离,纵轴表示相似度, 可以看到,对于较大相似度的点,t分布在低维空间中的距离需要稍小一点;而对于低相似度的点,t分布在低维空间中的距离需要更远。这恰好满足了我们的需求,即同一簇内的点(距离较近)聚合的更紧密,不同簇之间的点(距离较远)更加疏远。
总结一下,t-SNE的梯度更新有两大优势:
1.对于不相似的点,用一个较小的距离会产生较大的梯度来让这些点排斥开来。
2.这种排斥又不会无限大(梯度中分母),避免不相似的点距离太远。
算法过程
算法详细过程如下:
Data: X = x 1 , . . . , x n X = {x_1, ... , x_n} X=x1,...,xn
计算cost function的参数:困惑度Perp
优化参数: 设置迭代次数T, 学习速率\eta, 动量\alpha (t)
目标结果是低维数据表示 Y T = y 1 , . . . , y n Y^T = {y_1, ... , y_n} YT=y1,...,yn
开始优化
计算在给定Perp下的条件概率p_{j \mid i}参见上面公式)
令 p i j = p j ∣ i + p i ∣ j 2 n p_{ij} = \frac{p_{j \mid i} + p_{i \mid j}}{2n} pij=2npj∣i+pi∣j
用 N ( 0 , 1 0 − 4 I ) N(0, 10^{-4}I) N(0,10−4I) 随机初始化 Y Y Y
迭代,从 t = 1 到 T, 做如下操作:
计算低维度下的 q i j q_{ij} qij参见上面的公式)
计算梯度(参见上面的公式)
更新 Y t = Y t − 1 + η d C d Y + α ( t ) ( Y t − 1 − Y t − 2 ) Y^{t} = Y^{t-1} + \eta \frac{dC}{dY} + \alpha(t)(Y^{t-1} - Y^{t-2}) Yt=Yt−1+ηdYdC+α(t)(Yt−1−Yt−2)
结束
结束
优化过程中可以尝试的两个trick:
1.提前压缩(early compression):开始初始化的时候,各个点要离得近一点。这样小的距离,方便各个聚类中心的移动。可以通过引入L2正则项(距离的平方和)来实现。
2.提前夸大(early exaggeration):在开始优化阶段,p i j _{ij} ij乘以一个大于1的数进行扩大,来避免因为 q i j q_{ij} qij 太小导致优化太慢的问题。比如前50次迭代, p i j p_{ij} pij乘以4.
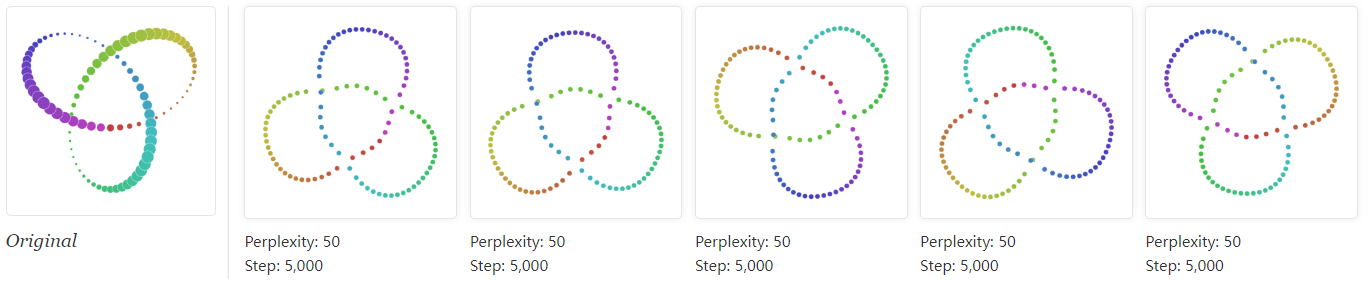
优化过程动态表示:
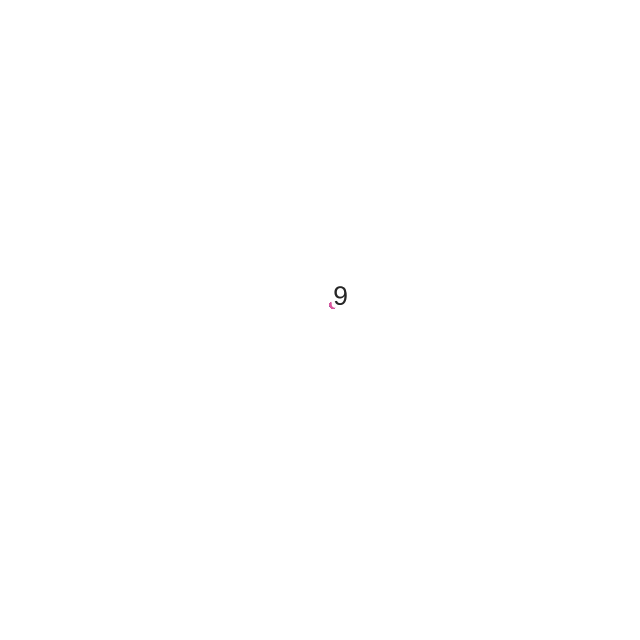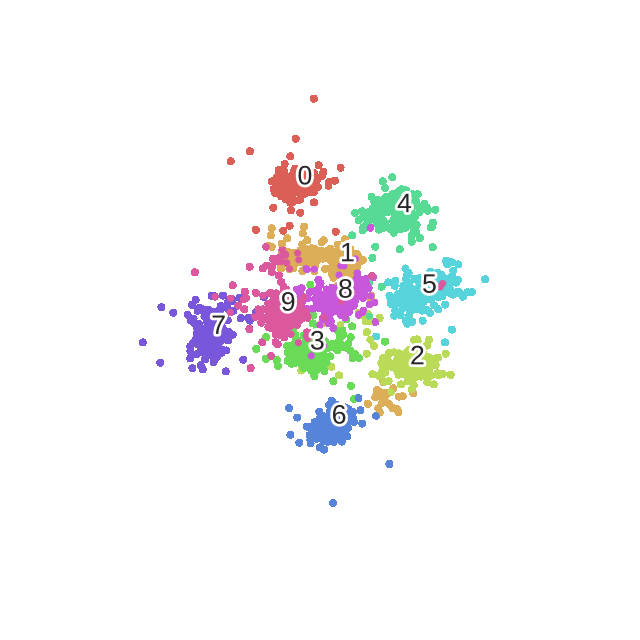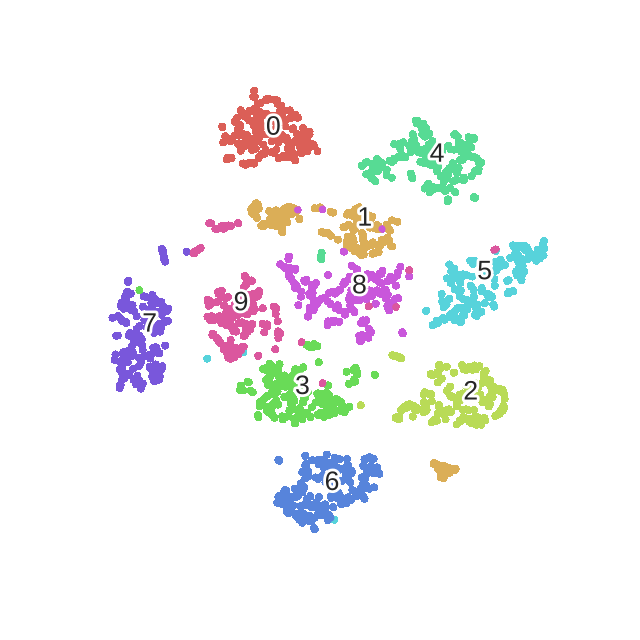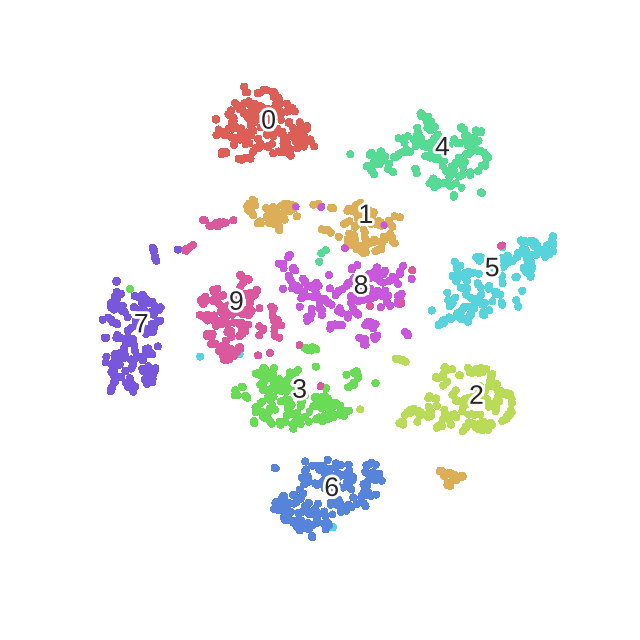
主要不足
主要不足有四个:
● 主要用于可视化,很难用于其他目的。比如测试集合降维,因为他没有显式的预估部分,不能在测试集合直接降维;比如降维到10维,因为t分布偏重长尾,1个自由度的t分布很难保存好局部特征,可能需要设置成更高的自由度。
● t-SNE倾向于保存局部特征,对于本征维数(intrinsic dimensionality)本身就很高的数据集,不可能完整的映射到2-3维的空间
● t-SNE没有唯一最优解,且没有预估部分。如果想要做预估,可以考虑降维之后,再构建一个回归方程之类的模型去做。但是要注意,t-sne中距离本身是没有意义,都是概率分布问题。
● 训练太慢。有很多基于树的算法在t-sne上做一些改进
代码
from time import time
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import offsetbox
from sklearn import (manifold, datasets, decomposition, ensemble,discriminant_analysis, random_projection)
digits = datasets.load_digits(n_class=10) #导入数据集
X = digits.data
y = digits.target
n_samples, n_features = X.shape
n_neighbors = 30
def plot_embedding(X, title=None):x_min, x_max = np.min(X, 0), np.max(X, 0)X = (X - x_min) / (x_max - x_min)plt.figure()ax = plt.subplot(111)for i in range(X.shape[0]):plt.text(X[i, 0], X[i, 1], str(digits.target[i]),color=plt.cm.Set1(y[i] / 10.),fontdict={'weight': 'bold', 'size': 9})if hasattr(offsetbox, 'AnnotationBbox'): #(用于判断对象是否包含对应的属性)shown_images = np.array([[1., 1.]])for i in range(digits.data.shape[0]):dist = np.sum((X[i] - shown_images) ** 2, 1)if np.min(dist) < 4e-3:continueshown_images = np.r_[shown_images, [X[i]]] #按列连接两个矩阵,就是把两矩阵上下相加,要求列数相等imagebox = offsetbox.AnnotationBbox(offsetbox.OffsetImage(digits.images[i], cmap=plt.cm.gray_r),X[i])ax.add_artist(imagebox)plt.xticks([]), plt.yticks([])if title is not None:plt.title(title)#----------------------------------------------------------------------n_img_per_row = 20
img = np.zeros((10 * n_img_per_row, 10 * n_img_per_row))
for i in range(n_img_per_row):ix = 10 * i + 1for j in range(n_img_per_row):iy = 10 * j + 1img[ix:ix + 8, iy:iy + 8] = X[i * n_img_per_row + j].reshape((8, 8))
plt.imshow(img, cmap=plt.cm.binary)
plt.xticks([])
plt.yticks([])
plt.title('A selection from the 64-dimensional digits dataset')
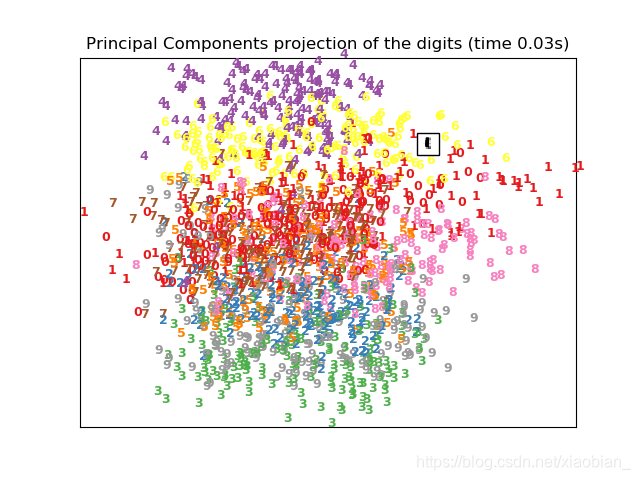
# 计算PCA
print("Computing PCA projection")
t0 = time()
X_pca = decomposition.TruncatedSVD(n_components=2).fit_transform(X)
plot_embedding(X_pca,"Principal Components projection of the digits (time %.2fs)" %(time() - t0))
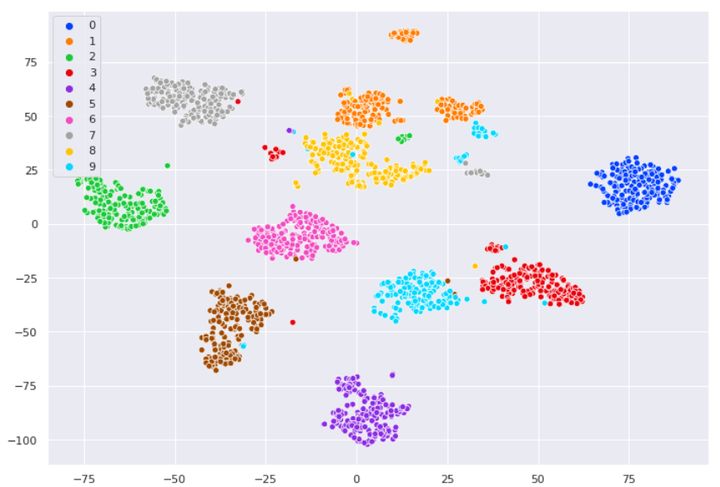
# 计算t-SNE
print("Computing t-SNE embedding")
tsne = manifold.TSNE(n_components=2, init='pca', random_state=0)
t0 = time()
X_tsne = tsne.fit_transform(X)
plot_embedding(X_tsne,"t-SNE embedding of the digits (time %.2fs)" %(time() - t0))
plt.show()