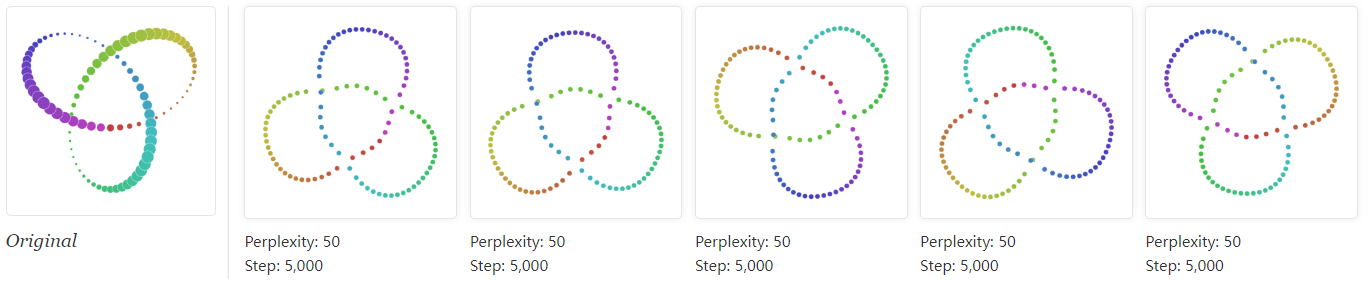
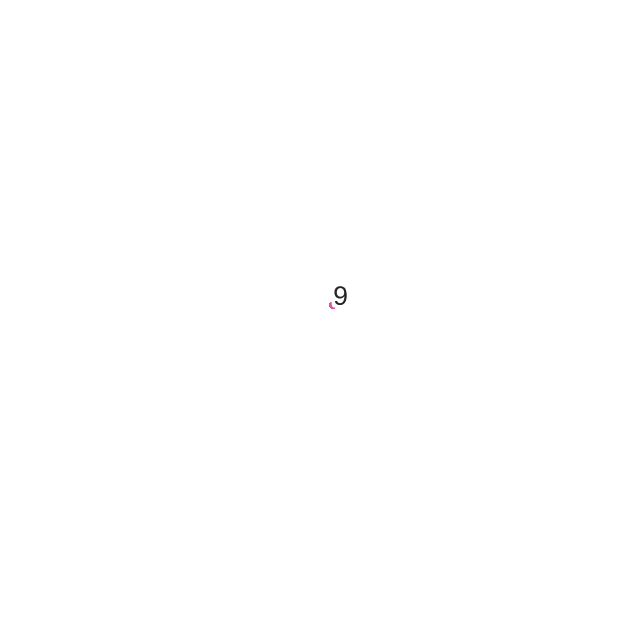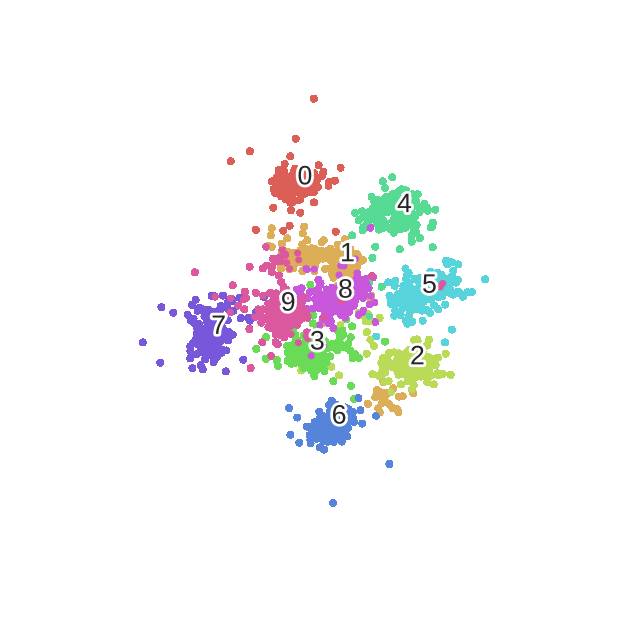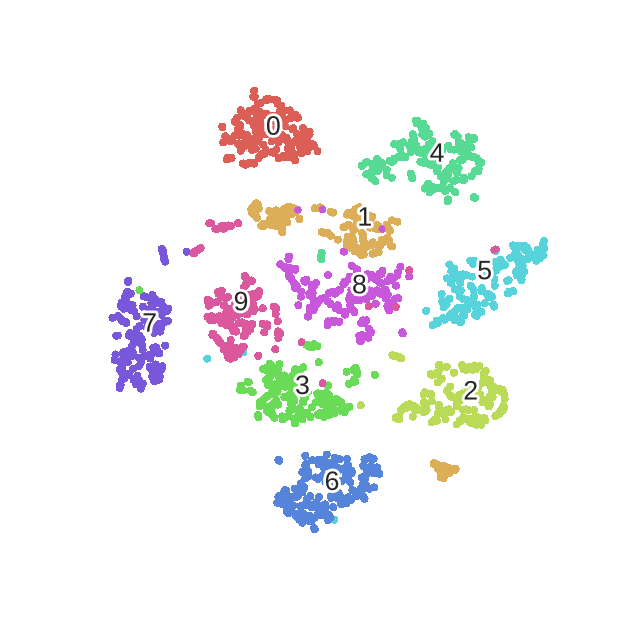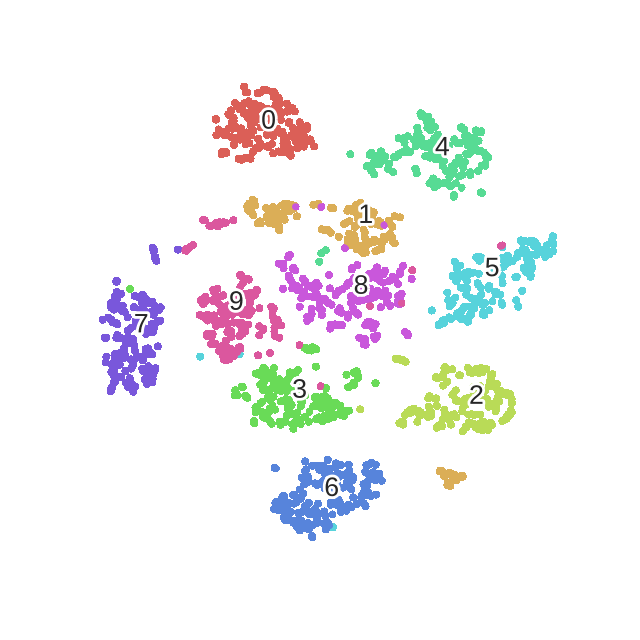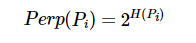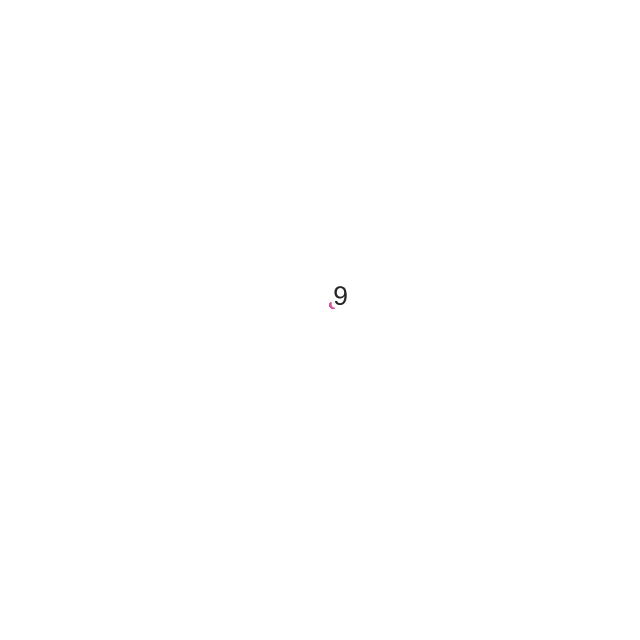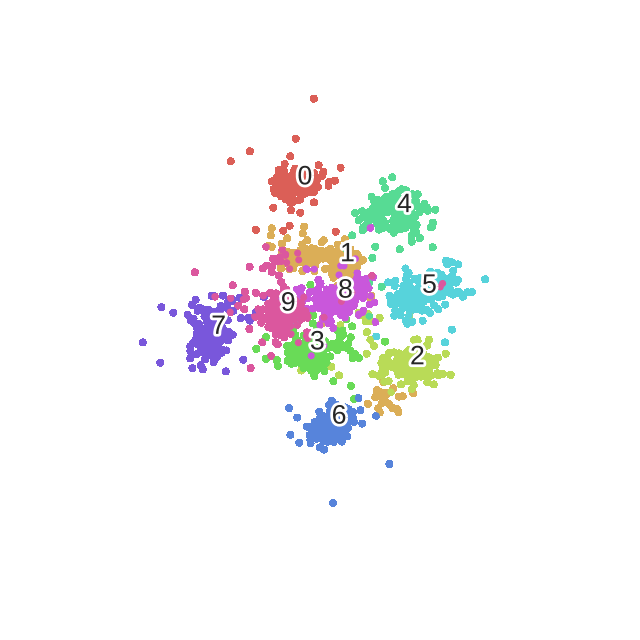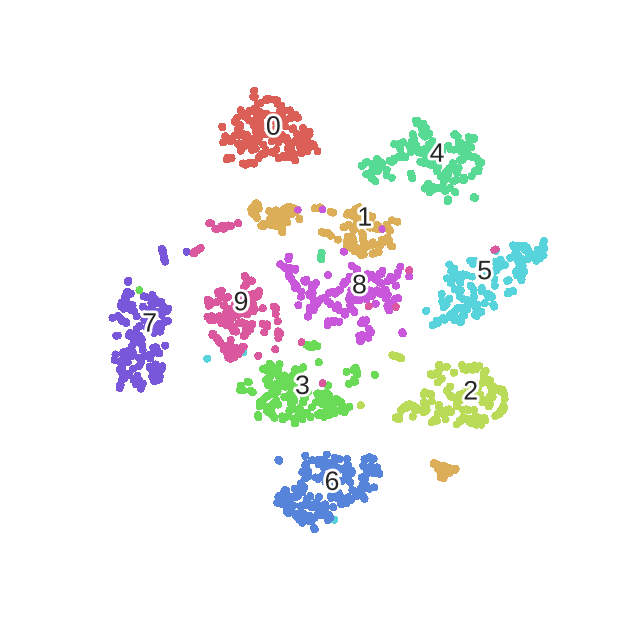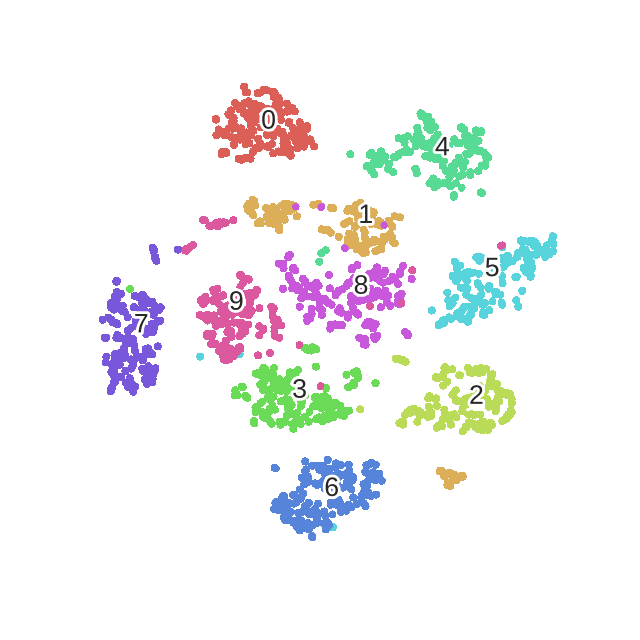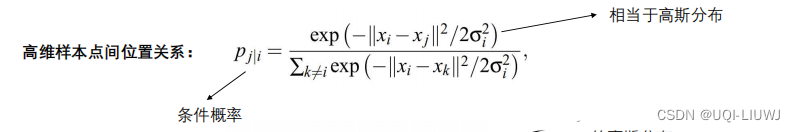t-SNE是一种经典的降维和可视化方法，是基于SNE（Stochastic Neighbor Embedding，随机近邻嵌入）做的，要了解t-SNE就要先了解SNE。本文同样既是总结，又是读论文笔记。

SNE 随机近邻嵌入

SNE的的第一步是用条件概率来表示高维空间中样本点之间用欧氏距离度量的相似度。假设样本选择其近邻的概率与与以自身为中心的高斯分布的概率密度成正比，SNE用$p_{j|i}$来表示高维空间样本$x_i$会选择$x_j$作为其近邻的概率，二范数距离越近，$p_{j|i}$越大，二范数距离越远，$p_{j|i}$越小。回忆一下高斯分布的概率密度函数：
$$f(x)=\frac{1}{\sqrt{2\pi }\sigma }\exp (-\frac{(x-\mu {)}^2}{2{\sigma }^2})$$

$p_{j|i}$定义为：
$$p_{j|i}=\frac{\exp (-\Vert x_i-x_j{\Vert }^2/2{\sigma }_i^2)}{{\sum }_{k\ne i}\exp (-\Vert x_i-x_k{\Vert }^2/2{\sigma }_i^2)}$$

其中${\sigma }_i^2$是以$x_i$为中心的高斯分布的方差，其取值后面再给出。由于只对成对样本的相似性感兴趣，SNE令$p_{i|i}=0$。
对于$x_i,x_j$对应的低位表示$y_i,y_j$，用$q_{j|i}$表示含义相似的条件概率，不同的是这里方差取$1/\sqrt{2}$，因此：
$$q_{j|i}=\frac{\exp (-\Vert y_i-y_j{\Vert }^2)}{{\sum }_{k\ne i}\exp (-\Vert y_i-y_k{\Vert }^2)}$$

同样令$q_{j|i}=0$。如果$y_i,y_j$能够正确地表征高维样本$x_i,x_j$之间的相似性，$p_{j|i},q_{j|i}$就应该相等，因此SNE的目标就是寻找恰当的高维样本的低维表示使得$p_{j|i},q_{j|i}$之间的比例失当最小。损失函数$C$用Kullback-Leibler divergence（K-L散度，互熵，文中说此处的kl熵等价于交叉熵加了一个参数）来表示：
$$C=\sum _{i}KL(P_i||Q_i)=\sum _i\sum _j{p}_{j|i}\log \frac{p_{j|i}}{q_{j|i}}\text{\hspace{1em}(1)}$$

然后SNE用梯度下降法来求解。由于K-L散度不是对称的，$C(p\Vert q)\ne C(q\Vert p)$，因此低维映射中成对的距离的不同类型误差不是以同一权重度量的。从$C$的定义来看，$p_{j|i}$较大时，期望寻找的$q_{j|i}$也是较大的，$p_{j|i}$较小时则无所谓。这说明SNE关注的主要还是如何保持局部结构（如果方差${\sigma }_i^2$取值合适的话）。

接下来的问题就是设置方差值${\sigma }_i^2$。SNE认为，在样本点分布比较稠密的区域，应该选择更小的方差值，否则反之。SNE设置了一个由用户调节的参数$Perp(P_i)$来衡量混乱度，其定义为：
$$\begin{gathered} Perp(P_i)=2^{H(P_i)} \\ H(P_i)=-\sum _j{p}_{j|i}{\log }_2{p}_{j|i} \end{gathered}$$

$H(P_i)$是$P_i$以二进制度量的香农熵。这是什么意思呢，我感觉意思就是由用户给定一个$Perp(P_i)$值，然后SNE给出了$Perp(P_i)$与$p_{j|i}$的关系，根据这个关系，用二分查找的方法来确定${\sigma }_i^2$。
混乱度参数可以平滑地度量有效的近邻数量，典型取值范围在5到50之间，从实验效果来看，SNE对混乱度参数的取值比较鲁棒。

SNE最小化公式$(1)$的过程是用梯度下降法来实现的，其导数惊人的简单：
$$\frac{\partial C}{\partial y_i}=2\sum _j(p_{j|i}-q_{j|i}+p_{i|j}-q_{i|j})(y_i-y_j)$$

我来试着求一下：
$$\begin{gathered} \frac{\partial C}{\partial q_{j|i}}=-p_{j|i}\frac{q_{j|i}}{p_{j|i}}\cdot \frac{p_{j|i}}{q_{j|i}^2}=-\frac{p_{j|i}}{q_{j|i}} \\ {q}_{j|i}=\frac{\exp (-\Vert y_i-y_j{\Vert }^2)}{{\sum }_{k\ne i}\exp (-\Vert y_i-y_k{\Vert }^2)} \\ \frac{\partial q_{j|i}}{\partial y_i}=\frac{{\exp }^{\prime }(-\Vert y_i-y_j{\Vert }^2)\cdot {\sum }_{k\ne i}\exp (-\Vert y_i-y_k{\Vert }^2)-{\sum }_{k\ne i}^{\prime }\exp (-\Vert y_i-y_k{\Vert }^2)\cdot \exp (-\Vert y_i-y_j{\Vert }^2)}{[{\sum }_{k\ne i}\exp (-\Vert y_i-y_k{\Vert }^2){]}^2} \\ =\frac{{\sum }_{k\ne i}\exp (-\Vert y_i-y_k{\Vert }^2)(2y_i-2y_k)\cdot \exp (-\Vert y_i-y_j{\Vert }^2)-\exp (-\Vert y_i-y_j{\Vert }^2)(2y_i-2y_j)\cdot {\sum }_{k\ne i}\exp (-\Vert y_i-y_k{\Vert }^2)}{[{\sum }_{k\ne i}\exp (-\Vert y_i-y_k{\Vert }^2){]}^2} \\ \frac{p_{j|i}}{q_{j|i}}\frac{\partial q_{j|i}}{\partial y_i}=p_{j|i}\frac{{\sum }_{k\ne i}\exp (-\Vert y_i-y_k{\Vert }^2)(2y_i-2y_k)-(2y_i-2y_j)\cdot {\sum }_{k\ne i}\exp (-\Vert y_i-y_k{\Vert }^2)}{{\sum }_{k\ne i}\exp (-\Vert y_i-y_k{\Vert }^2)} \\ =p_{j|i}[\sum _{k\ne i}{q}_{k|i}2(y_i-y_k)-2(y_i-y_j)] \\ =2p_{j|i}[q_{j|i}-1](y_i-y_j)+p_{j|i}\sum _{k\ne i,j}{q}_{k|i}2(y_i-y_k) \\ {q}_{i|j}=\frac{\exp (-\Vert y_j-y_i{\Vert }^2)}{{\sum }_{k\ne j}\exp (-\Vert y_j-y_k{\Vert }^2)} \\ \frac{\partial q_{i|j}}{\partial y_i}=\frac{\exp (-\Vert y_j-y_i{\Vert }^2)(2y_j-2y_i)\cdot \exp (-\Vert y_j-y_i{\Vert }^2)-\exp (-\Vert y_j-y_i{\Vert }^2)(2y_j-2y_i)\cdot {\sum }_{k\ne j}\exp (-\Vert y_j-y_k{\Vert }^2)}{[{\sum }_{k\ne j}\exp (-\Vert y_j-y_k{\Vert }^2){]}^2} \\ \frac{p_{i|j}}{q_{i|j}}\frac{\partial q_{i|j}}{\partial y_i}=p_{i|j}\frac{(2y_j-2y_i)\exp (-\Vert y_j-y_i{\Vert }^2)-(2y_j-2y_i)\cdot {\sum }_{k\ne j}\exp (-\Vert y_j-y_k{\Vert }^2)}{{\sum }_{k\ne j}\exp (-\Vert y_j-y_k{\Vert }^2)} \\ =p_{i|j}[(2y_j-2y_i)q_{i|j}-2(y_j-y_i)] \\ =2p_{i|j}(q_{i|j}-1)(y_j-y_i) \\ \frac{\partial C}{\partial y_i}=-\sum _j(\frac{p_{j|i}}{q_{j|i}}\frac{\partial q_{j|i}}{\partial y_i}+\frac{p_{i|j}}{q_{i|j}}\frac{\partial q_{i|j}}{\partial y_i}) \end{gathered}$$

不好意思我求不出来。

继续看论文。物理上看，这个梯度可以理解为$y_i$和所有其他的$y_j$之间存在的“流（spring）”合在一起构成的合力，所有的流构成了沿着$y_i-y_j$方向的合力。$y_i,y_j$之间的流是否抵制或吸引样本点，取决于二者之间的距离是否会过大或过小地表示$x_i,x_j$之间的距离。
为了避免局部最优解，SNE还给梯度添加了一项很大的动量项。换句话来讲，当前的梯度被加上了一项指数衰减的之前的梯度：
$${\mathcal{Y}}^{(t)}={\mathcal{Y}}^{(t-1)}+\eta \frac{\partial C}{\partial \mathcal{Y}}+\alpha (t)({\mathcal{Y}}^{(t-1)}-{\mathcal{Y}}^{(t-2)})$$

其中${\mathcal{Y}}^{(t)}$表示当前迭代轮次的解，$\eta$为学习率，$\alpha (t)$表示当前迭代轮次的动量。
在优化刚开始的时候，每次迭代都会给样本点添加高斯噪声，可以起到一个退火的效果，避免局部最优解。如果噪声的方差改变缓慢，SNE就可以寻找到更好的全局最优解。然而这对噪声数量和衰减速率很敏感，往往需要在一个数据集上训练多次以寻找合适的参数，从这个意义上讲SNE不如一些可以遵循凸优化原则的方法，如果能找到一种不需要额外计算和参数的方法就更好了。这样就引出了t-SNE。

Hinton发明的这个SNE跟神经网络的一些做法都很相似了。t-SNE作者在论文里对SNE的批评也和对多数神经网络的批评一样。我读着这些东西都快要走到深度学习的路上去了。

对称SNE

t-SNE（t-Distributed Stochastic Neighbor Embedding，t分布的SNE）的目标是优化SNE的上述缺点。与SNE不同的是，t-SNE的损失函数（1）是对称的，且有更简单的梯度；（2）使用t分布（Student-t distribution）而非高斯分布来样本在低维空间的相似性。t-SNE在低维空间使用重尾分布（heavy-tailed distribution）来缓解SNE的弊端。

$C$的定义不变：
$$C=\sum _{i}KL(P_i||Q_i)=\sum _i\sum _j{p}_{ij}\log \frac{p_{ij}}{q_{ij}}$$

同样令$p_{ii}=q_{ii}=0$，不过t-SNE希望$p_{ij}=p_{ji},q_{ij}=q_{ji}$，即具有对称性。因此定义：
$$\begin{gathered} p_{ij}=\frac{\exp (-\Vert x_i-x_j{\Vert }^2/2{\sigma }^2)}{{\sum }_{k\ne l}\exp (-\Vert x_k-x_l{\Vert }^2/2{\sigma }^2)} \\ {q}_{ij}=\frac{\exp (-\Vert y_i-y_j{\Vert }^2)}{{\sum }_{k\ne l}\exp (-\Vert y_k-y_l{\Vert }^2)} \end{gathered}$$

但是这样会造成一个问题，如果$x_i$是个outlier（即如果所有其他样本距离它的距离都很远），$p_{ij}$就会很小，此时$x_i$对$C$就只有很小的影响，也就是说除了$y_i$的位置并没有很好地被其他样本影响。为了规避这个问题，令$p_{ij}=\frac{p_{j|i}+p_{i|j}}{2n}$，这样对于所有的样本点$x_i$都保证了${\sum }_j{p}_{ij}>\frac{1}{2n}$，每个样本点都能对损失函数$C$产生显著影响。而且这样一来梯度公式就会更简单：
$$\frac{\partial C}{\partial y_i}=4\sum _j(p_{ij}-q_{ij})(y_i-y_j)$$

我来试着求一下：
$$\begin{gathered} \frac{\partial C}{\partial y_i}=-\sum _j(\frac{p_{ij}}{q_{ij}}\frac{\partial q_{ij}}{\partial y_i}+\frac{p_{ji}}{q_{ji}}\frac{\partial q_{ji}}{\partial y_i}) \\ \frac{\partial q_{ij}}{\partial y_i}=-q_{ij}\cdot 2(y_i-y_j) \\ \frac{\partial q_{ji}}{\partial y_i}=-q_{ji}\cdot 2(y_j-y_i)=q_{ji}\cdot 2(y_i-y_j) \\ \frac{\partial C}{\partial y_i}=\sum _j[p_{ij}\cdot 2(y_i-y_j)-p_{ji}\cdot 2(y_i-y_j)]=2\sum _j(p_{ij}-p_{ji})(y_i-y_j) \end{gathered}$$

还是求不出来。后面再看看吧。继续读论文。

文章提出了一个开创性的观点：“crowding problems”：如果高维空间中有许多点均匀地分布在样本$i$周围，并且现在希望将这些点映射到二维空间中，那么在二维空间中可得的能够容纳适度远的点的区域将没有可以容纳临近点的区域大。因此，如果我们希望在二维空间准确地描述较小的距离，就必须把样本$i$周围适当距离的点放到二维空间更远的距离上。

t-SNE

t-SNE使用的是只有一个自由度的Student t分布（与柯西分布相同）来定义$q_{ij}$：
$$q_{ij}=\frac{(1+\Vert y_i-y_j{\Vert }^2{)}^{-1}}{{\sum }_{k\ne l}(1+\Vert y_k+y_l{\Vert }^2{)}^{-1}}$$

这东西的好处在于，使得联合概率的表示对于样本在高维和低维空间距离尺度的变化几乎不敏感，而且大的比较分散的点集就像独立的点一样互相作用，其优化操作与SNE和对称SNE相同，但是尺度更合适。一种理论支持是，Student t分布是高斯分布的无穷混合，与高斯分布非常接近。而且由于没有指数项，Student t分布也会让计算更方便。偏导直接给出：
$$\frac{\partial C}{\partial y_i}=4\sum _j(p_{ij}-q_{ij})(y_i-y_j)(1+\Vert y_i-y_j{\Vert }^2{)}^{-1}$$

t-SNE总体流程如下：

文章说t-SNE的效果还可以通过两个trick进一步提高。一是“提前压缩”，即在优化开始前令样本全都聚集在一起，这样便于样本簇互相移动穿越，并且更便于寻找全局最优。