LIS定义

LIS（Longest Increasing Subsequence）最长上升子序列 
一个数的序列bi，当b1 < b2 < … < bS的时候，我们称这个序列是上升的。

对于给定的一个序列(a1, a2, …, aN)，我们可以得到一些上升的子序列(ai1, ai2, …, aiK)，

这里1 <= i1 < i2 < … < iK <= N。 
比如，对于序列(1, 7, 3, 5, 9, 4, 8)，有它的一些上升子序列，如(1, 7), (3, 4, 8)等等。

这些子序列中最长的长度是4，比如子序列(1, 3, 5, 8). 
你的任务，就是对于给定的序列，求出最长上升子序列的长度。

两种做法

O(N^2)做法：dp动态规划

状态设计：dp[i]代表以a[i]结尾的LIS的长度 
状态转移：dp[i]=max(dp[i], dp[j]+1) (0<=j< i, a[j]< a[i]) 
边界处理：dp[i]=1 (0<=j< n) 
时间复杂度：O(N^2) 
举例： 对于序列(1, 7, 3, 5, 9, 4, 8)，dp的变化过程如下

dp[i]	初始值	j=0	j=1	j=2	j=3	j=4	j=5
dp[0]	1
dp[1]	1	2
dp[2]	1	2	2
dp[3]	1	2	2	3
dp[4]	1	2	3	3	4
dp[5]	1	2	2	3	3	3
dp[6]	1	2	3	3	4	4	4

求完dp数组后，取其中的最大值就是LIS的长度。【注意答案不是dp[n-1]，这个样例只是巧合】

#include<stdio.h>
#include<iostream>
#include<string.h>
#include<queue>
#include<cstdio>
#include<string>
#include<math.h>
#include<algorithm>
#include<map>
#include<set>
#include<stack>
#define mod 998244353
#define INF 0x3f3f3f3f
#define eps 1e-6
using namespace std;
typedef long long ll;
using namespace std;
const int MAXX=10000+5;int a[MAXX],dp[MAXX];
// a数组为数据，dp[i]表示以a[i]结尾的最长递增子序列长度
int n;
int LIS(){int ans=1;for(int i=1; i<=n; i++)//枚举子序列的终点{dp[i]=1;// 初始化为1，长度最短为自身for(int j=1; j<i; j++)//从头向终点检查每一个元素{if(a[i]>a[j]){dp[i]=max(dp[i],dp[j]+1);  // 状态转移}}ans=max(ans,dp[i]);  // 比较每一个dp[i],最大值为答案}return ans;
}
int main()
{while(cin>>n){for(int i=1; i<=n; i++){cin>>a[i];}int ans=LIS();cout<<ans<<endl;}return 0;
}

O(NlogN)做法：贪心+二分

a[i]表示第i个数据。 
dp[i]表示表示长度为i+1的LIS结尾元素的最小值。 
利用贪心的思想，对于一个上升子序列，显然当前最后一个元素越小，越有利于添加新的元素，这样LIS长度自然更长。 
因此，我们只需要维护dp数组，其表示的就是长度为i+1的LIS结尾元素的最小值，保证每一位都是最小值，

这样子dp数组的长度就是LIS的长度。

dp数组具体维护过程同样举例讲解更为清晰。 
同样对于序列 a(1, 7, 3, 5, 9, 4, 8)，dp的变化过程如下：

• dp[0] = a[0] = 1，长度为1的LIS结尾元素的最小值自然没得挑，就是第一个数。 （dp = {1}）
• 对于a[1]=7，a[1]>dp[0]，因此直接添加到dp尾，dp[1]=a[1]。（dp = {1, 7}）
• 对于a[2]=3，dp[0]< a[2]< dp[1]，因此a[2]替换dp[1]，令dp[1]=a[2]，因为长度为2的LIS，结尾元素自然是3好过于7，因为越小这样有利于后续添加新元素。 （dp = {1, 3}）
• 对于a[3]=5，a[3]>dp[1]，因此直接添加到dp尾，dp[2]=a[3]。 （dp = {1, 3, 5}）
• 对于a[4]=9，a[4]>dp[2]，因此同样直接添加到dp尾，dp[3]=a[9]。 （dp = {1, 3, 5, 9}）
• 对于a[5]=4，dp[1]< a[5]< dp[2]，因此a[5]替换值为5的dp[2]，因此长度为3的LIS，结尾元素为4会比5好，越小越好嘛。（dp = {1, 3, 4, 9}）
• 对于a[6]=8，dp[2]< a[6]< dp[3]，同理a[6]替换值为9的dp[3]，道理你懂。 （dp = {1, 3, 5, 8}）

这样子dp数组就维护完毕，所求LIS长度就是dp数组长度4。 
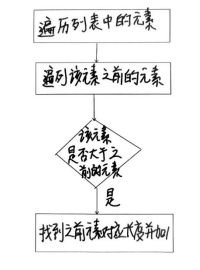
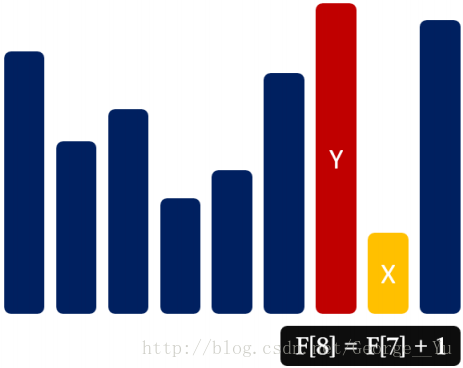
通过上述求解，可以发现dp数组是单调递增的，因此对于每一个a[i]，先判断是否可以直接插入到dp数组尾部，

即比较其与dp数组的最大值即最后一位；如果不可以，则找出dp中第一个大于等于a[i]的位置，用a[i]替换之。 
这个过程可以利用二分查找，因此查找时间复杂度为O(logN)，所以总的时间复杂度为O(N*logN)

#include <bits/stdc++.h>
using namespace std;
const int MAXX=100000+5;
const int INF=INT_MAX;int a[MAXX],dp[MAXX]; // a数组为数据，dp[i]表示长度为i+1的LIS结尾元素的最小值int main()
{int n;while(cin>>n){for(int i=0; i<n; i++){cin>>a[i];dp[i]=INF; // 初始化为无限大}int pos=0;    // 记录dp当前最后一位的下标dp[0]=a[0];   // dp[0]值显然为a[0]for(int i=1; i<n; i++){if(a[i]>dp[pos])    // 若a[i]大于dp数组最大值，则直接添加dp[++pos] = a[i];else    // 否则找到dp中第一个大于等于a[i]的位置，用a[i]替换之。dp[lower_bound(dp,dp+pos+1,a[i])-dp]=a[i];  // 二分查找}cout<<pos+1<<endl;}return 0;
}

最长上升子序列

，即整个序列严格递增

最长不下降子序列，也叫最长非递减子序列

HDU5532

把每个数字减去对应位置的编号，然后求最长非递减子序列长度即可

#include <cstdio>
#include <cstring>
#include <algorithm>
#include<iostream>
using namespace std;
#define INF 0x3f3f3f3f
typedef long long LL;
int n;
const int maxn=1e5+10;
int a[maxn],dp[maxn];
int LIS(){int pos=0;dp[0]=a[0];for(int i=1;i<n;i++){if(a[i]>=dp[pos])//改变1：将大于该为大于等于dp[++pos]=a[i];else//改变2：查询dp数组中第一个大于a[i]的位置，用a[i]代替dp[upper_bound(dp,dp+pos+1,a[i])-dp]=a[i];}return pos+1;
}
int main(){int T;scanf("%d",&T);int ca=1;while(T--){scanf("%d",&n);for(int i=0;i<n;i++){scanf("%d",&a[i]);a[i]-=i;dp[i]=INF;}int len=LIS();printf("Case #%d:\n",ca++);printf("%d\n",n-len);}return 0;
}