子序列
所谓的子序列就是在原来序列中找出一部分组成的序列。
与子段不同,不需要连续的某一段,但是要保持原序列的先后顺序

最长上升子序列
在子序列的基础上,后一项大于前一项。
【题目描述】

【输入格式】

【输出格式】

【输入样例】
12
35 42 4 12 29 21 29 11 1 42 43 49【输出样例】
7【数据范围】

分析
我们会想到用递推做。
对于递推,我们需要考虑以下几点
- 状态,即F[ i ]表示什么
- 递推式,即怎么由前面的项推出后面的项
- 答案
- 初始值
状态
我们给出一组数

方向一(错误):F[ i ]表示前 i 项的上升子序列的最大长度
那我们把F[ i ]写在第 i 项的上面

发现F[ i ]都能列出来,但是递推式完全出不来,前项和后项根本无法递推
方向二:F[ i ]表示以第 i 项为结尾的上升子序列的最大长度
得到:

这就可以递推了

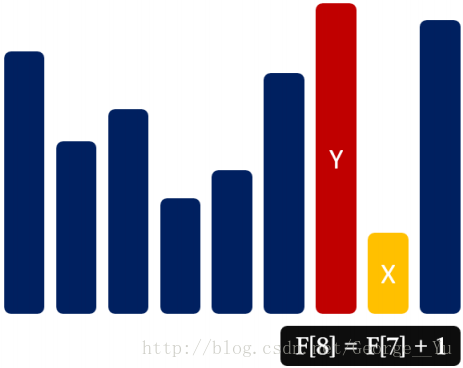
如果a[ j ] < a[ i ],那就可以形成上升子序列,则F[ i ]为F[ j ]+1和自己本身的较大数
如此循环,那
递推式
就很清楚了,就是:

答案
显而易见,F[ i ]中的最大值
初始值
如果都不符合a[ j ] < a[ i ],那么F[ i ]就是1
所以初始值是1而不是0
最后最后,
附上代码
#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;long long a[5010];
int f[5010];
//f[i]表示以第i项结尾的最长上升子序列
int main()
{int n;cin >> n;for(int i = 1;i <= n;i++){cin >> a[i];}int maxn = 0;for(int i = 1;i <= n;i++){f[i] = 1;//初值for(int j = 1;j <= i - 1;j++){if(a[j] < a[i])f[i] = max(f[i],f[j] + 1);maxn = max(maxn,f[i]);}}cout << maxn;return 0;
}



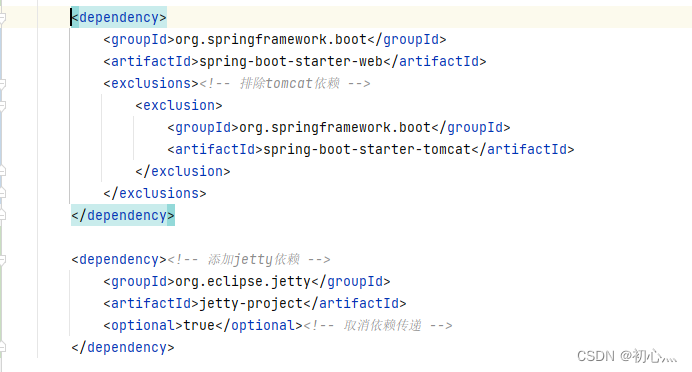
![[1120]Maven依赖冲突解决之exclusions](https://img-blog.csdnimg.cn/img_convert/701b4cfc6124f03d0d48f5efe5948359.png)