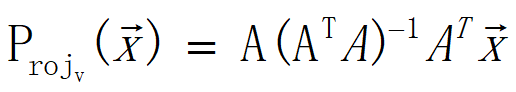一、概念比较
①人教A版:已知两个非零向量 与
与 ,我们把数量
,我们把数量 叫做
叫做 与
与 的数量积(或内积),记作
的数量积(或内积),记作 ,即
,即
 ,其中
,其中 是
是 与
与 的夹角,
的夹角, (
( )叫做向量
)叫做向量 在
在 方向上(
方向上( 在
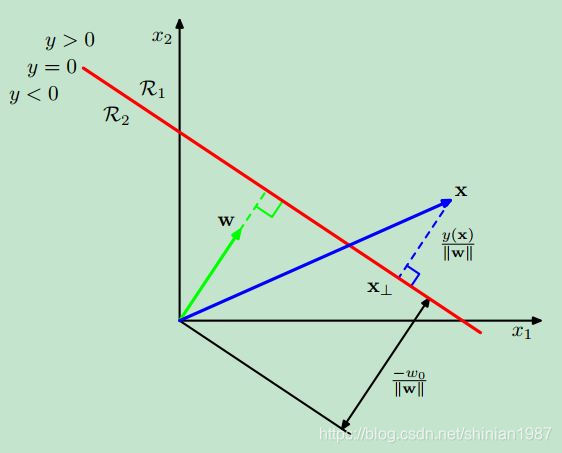
在 方向上)的投影(如下图)
方向上)的投影(如下图) 。
。

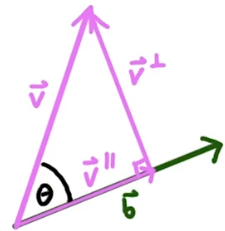
②人教B版:已知向量 和
和 轴(如下图)。作
轴(如下图)。作 ,过点
,过点 分别作轴
分别作轴 的垂线,垂足分别为
的垂线,垂足分别为 ,则
,则 叫做向量
叫做向量 在轴
在轴 上的正射影(简称射影),该射影在轴
上的正射影(简称射影),该射影在轴 上的坐标,称作
上的坐标,称作 在轴
在轴 上的数量或在轴
上的数量或在轴 的方向上的数量,记作
的方向上的数量,记作 。
。

二、概念异同
①不同点:向量的投影是一个实数;向量的射影是一个向量;二者不是同一类,求法各不同。

②相同点:向量投影与向量射影的数量是等价的;在数学上表示同一个意思,求法是相同的。

三、求解举例
【例题】已知三点 ,则向量
,则向量 在
在 方向上的投影为_________。
方向上的投影为_________。
【解析】向量 在
在 方向上的投影是实数,利用投影公式
方向上的投影是实数,利用投影公式 求解。
求解。
由 得:
得: ,
, ,利用投影公式可知:
,利用投影公式可知: 。
。
所以,向量 在
在 方向上的投影为
方向上的投影为 。
。
【变式】已知三点 ,则向量
,则向量 在
在 方向上的射影为_________。
方向上的射影为_________。
【解析】向量 在
在 方向上的射影是向量,利用公式求解。
方向上的射影是向量,利用公式求解。
由 得:
得: ,
, ,利用射影公式可知:
,利用射影公式可知: 所以,向量
所以,向量 在
在 方向上的射影为
方向上的射影为 。
。
注意:向量 在
在 方向上的投影为实数
方向上的投影为实数 ,向量
,向量 在
在 方向上的射影为向量
方向上的射影为向量 它们的类型显然是不同的;但向量
它们的类型显然是不同的;但向量 在
在 方向上射影的数量为实数
方向上射影的数量为实数 ,与向量
,与向量 在
在 方向上的投影为实数
方向上的投影为实数 是一回事儿!
是一回事儿!