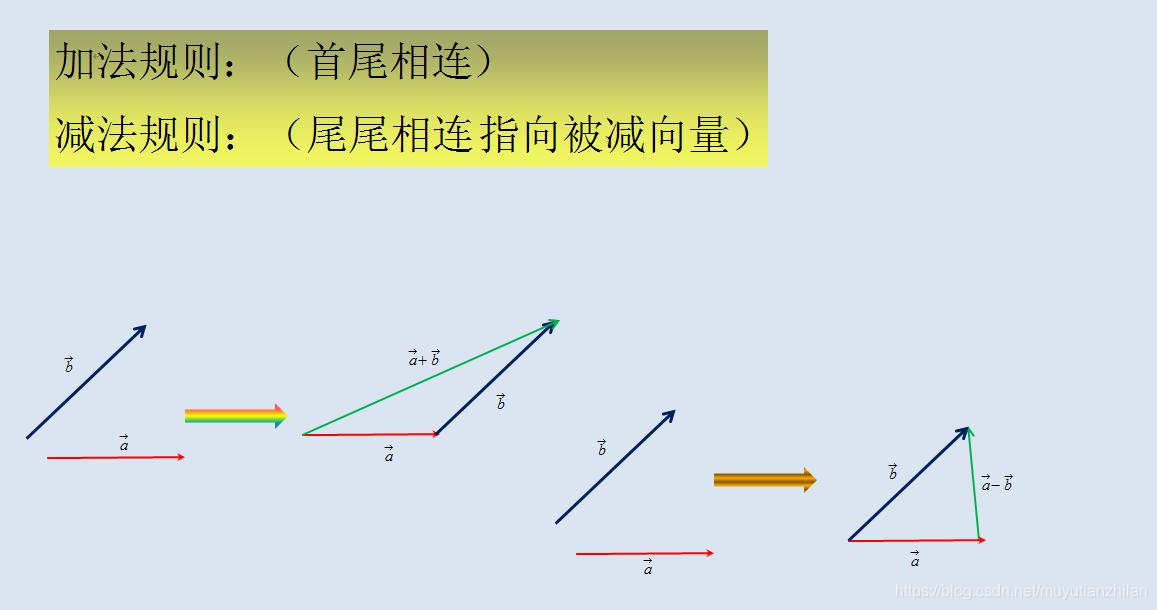
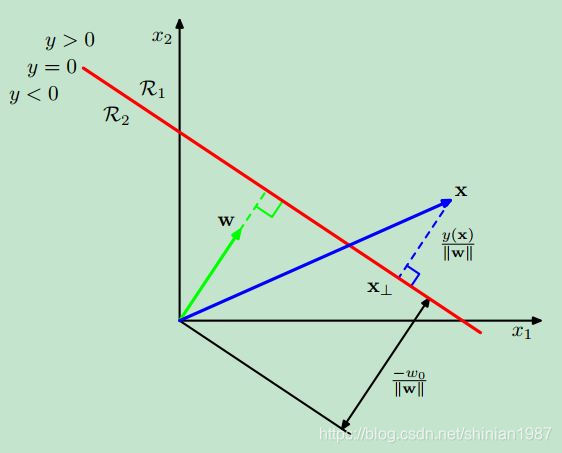
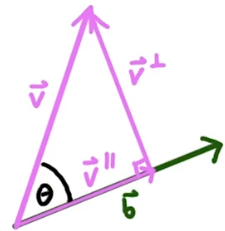
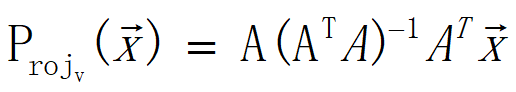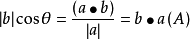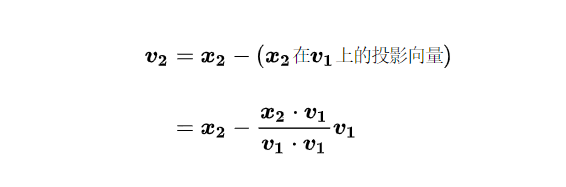1 定义 - ProjectOnPlane

 //
// 摘要:
//     Projects a vector onto a plane defined by a normal orthogonal to the plane.
//
// 参数:
//   planeNormal:
//     The direction from the vector towards the plane.
//
//   vector:
//     The location of the vector above the plane.
//
// 返回结果:
//     The location of the vector on the plane.
public static Vector3 ProjectOnPlane(Vector3 vector, Vector3 planeNormal);

2 使用方法

• 参数1 方向
• 参数2 平面的法向量

投影向量

var pj = Vector3.ProjectOnPlane(dir, normal);

返回值是一个投影向量，平行于指定的平面

3 效果演示

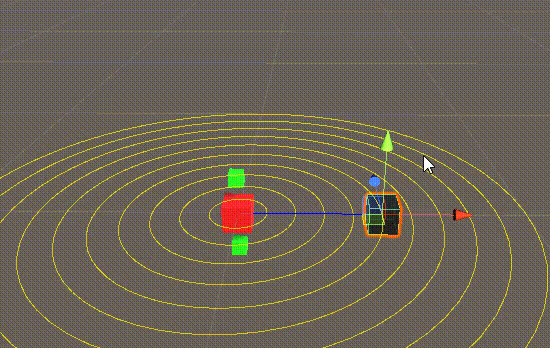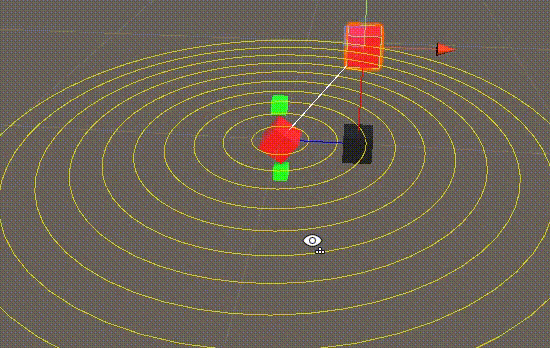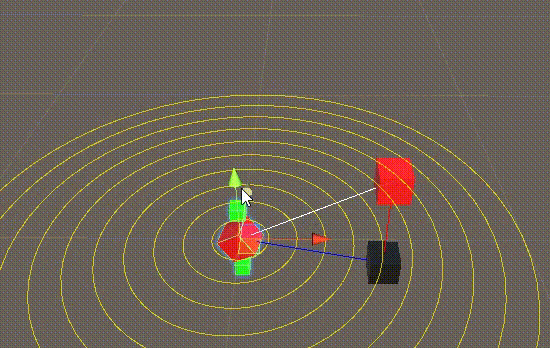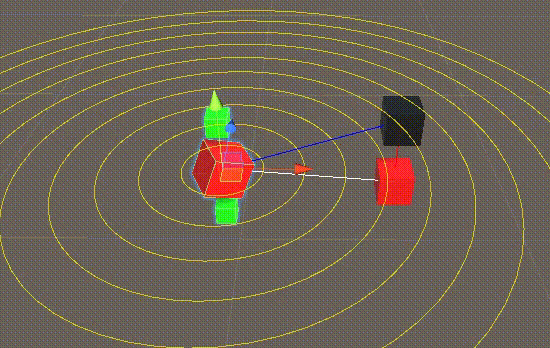
4 参考代码

using UnityEditor;
using UnityEngine;public class Pj : MonoBehaviour
{void Update(){project();}//方向向量目标点 看向点public Transform target,looker;//两点确定法线方向public Transform n1, n2;//跟随点public Transform sign;void project(){looker.transform.LookAt(target);//指向目标的向量var dir = target.position - transform.position;//平行于X轴平面的法向量 Y轴正方向向量 （1,0,0）var normal = n1.position - n2.position;//投影向量var pj = Vector3.ProjectOnPlane(dir, normal);//相对本对象位置进行变化sign.position = transform.position + pj;//绘制方向Debug.DrawLine(transform.position, target.position);//绘制投影Debug.DrawLine(transform.position, sign.position, Color.blue);//绘制法线Debug.DrawLine(target.position, sign.position,Color.red);}//绘制平面private void OnDrawGizmos(){//平行于X轴平面的法向量 Y轴正方向向量 （1,0,0）var dir = n1.position - n2.position;Handles.color = Color.yellow;for (int i = 0; i < 10; i++){var dis = i + 1;Handles.DrawWireDisc(transform.position, dir, dis * 0.1f);}}
}

5 工程包
链接

6 投影函数 Project

7 函数返回值
是vector向量 想X轴正方形进行投影，最终落在X轴的一个点