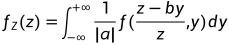前面， 我详细介绍了 一个随机变量函数的概率分布 ，本文开始介绍 两个随机变量的函数。

注意， 不能写成 两个随机变量函数， 那就会误认为 两个函数，

本文主要介绍两个连续型随机变量的函数， 至于离散型，由读者自行了解。

一 两个连续型随机变量

设X与Y为两个连续型随机变量，也可以说(X, Y)为二维连续型随机变量，f(x, y)为密度函数，

Z=X+Y. 则Z的概率密度

可以看到， 求Z的概率密度，在不确定X,Y是否相互独立，需要已知(X, Y)的密度函数f(x, y).

二 两个独立连续型随机变量，卷积公式

设(X, Y)是二维连续型随机变量，密度函数是f(x, y), X, Y的边缘密度分别为

设X与Y相互独立， 求Z=X+Y的概率密度。

分析： 因为X与Y相互独立， 有

所以， ,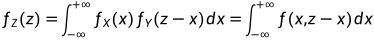

.

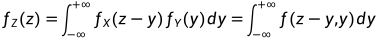这两个公式称为 独立随机变量和的卷积公式。 卷积公式是背记的重点， 必须牢牢记住， 必须掌握。

简单地说：x的密度乘以(z-x)为参数的y的密度，再对x求积分， 就是z的密度

或者 以(z-y)为参数的x的密度乘以y的密度， 再对y求积分， 就是z的密度。

可以看到， 哪个密度的参数简单，就对哪个积分。

现在，我们了解了卷积公式， 不再对这个概念陌生，

知道了卷积公式是应用于 两个独立连续型随机变量之和

三 例题

设二维随机变量(X, Y) 的概率密度为 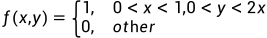, 求Z = 2X-Y的概率密度。

解： 求Z的概率密度， 即 ,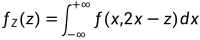

因为 0<y<2x, 即0<2x-z<2x, 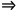-2x<z-2x<0, 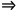0<z<2x,

所以

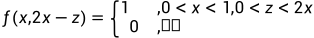
画出图，所示

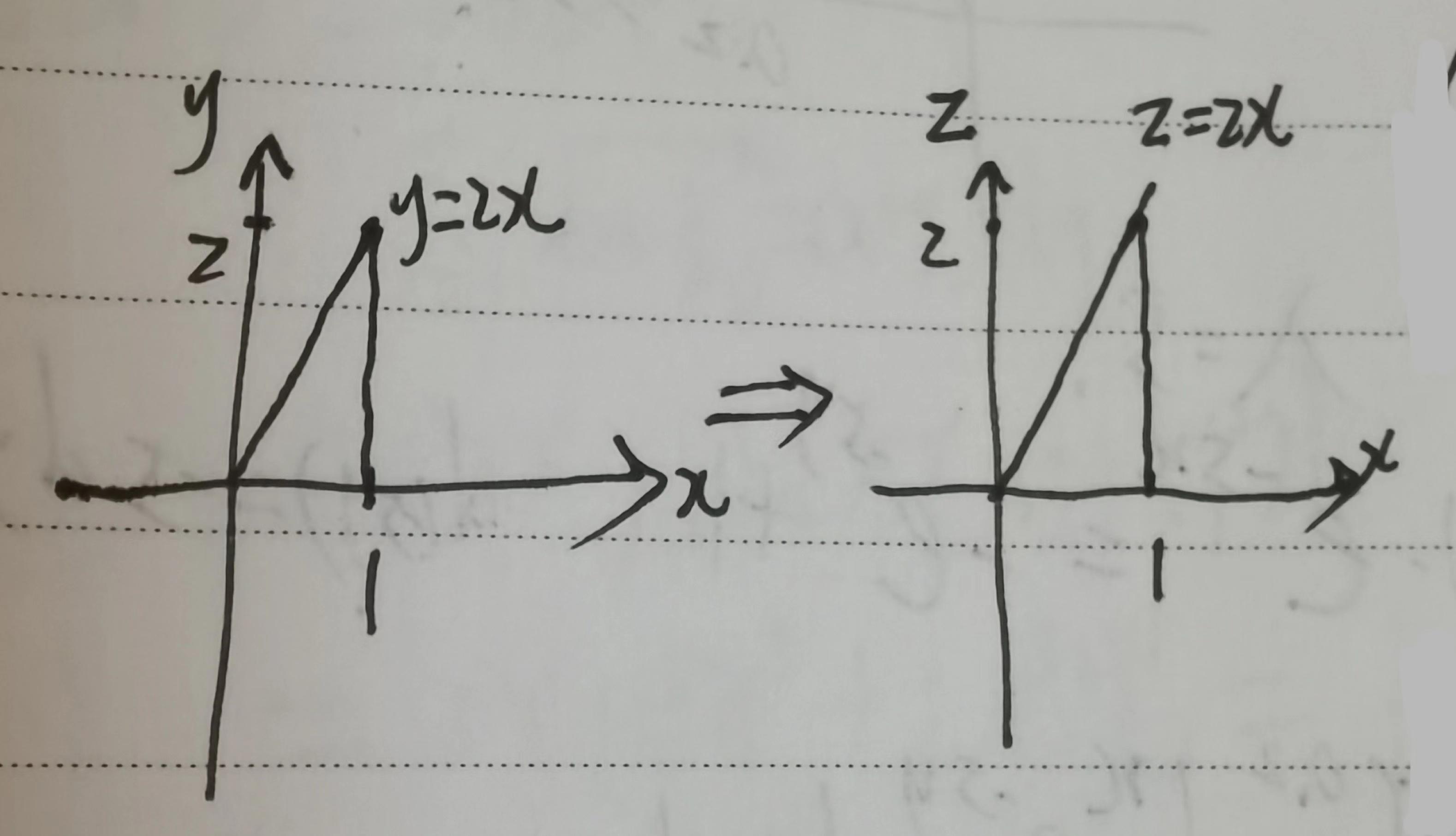
现在分情况讨论：

1. 当z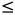0时， f(x, 2x-z)=0 (属于上述公式中 其他)

2. 当 z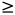2时， f(x, 2x-z)=0 (属于上述公式中 其他)

3. 0<z<2时，

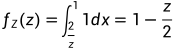
所以 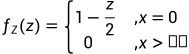， 这就是Z=2X-Y的概率密度。

题2 两个指数分布之和Z=X+Y, 称为Gamma分布

题 3， 下面的例题是 离散型 与 连续型的结合， 仔细看 解题过程。

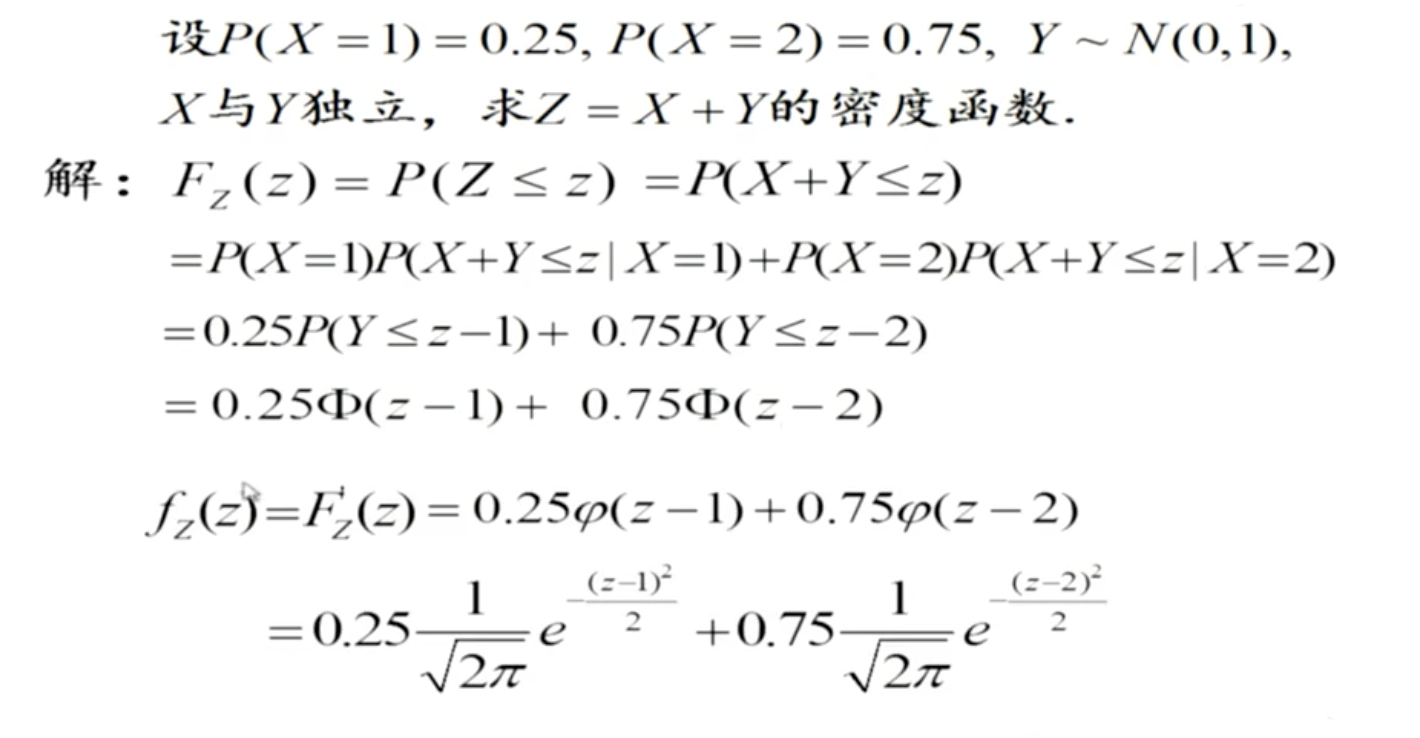
四 解题总结： 已知二维随机变量的分布函数， 求Z的分布函数

已知 （X, Y)的分布函数，Z= g(X, Y) = aX + bY， 求Z的密度函数。

方法一： 分布函数法

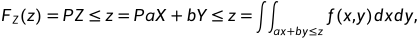
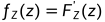
方法二: 公式法

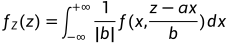，或者