MATLAB仿真
- 一、卡尔曼滤波的实际应用
- 二、流程图
- 三、执行过程
- 四、程序代码
- 五、仿真结果
- 参考文献
一、卡尔曼滤波的实际应用
在这里依旧以前面提到的测量硬币为例进行MATLAB仿真。现有一枚硬币为了这枚硬币的直径,我们进行了多次测量,但是所使用的的尺子存在一定误差,人进行测量的过程中存在测量误差,而且由常识可以估算硬币的直径得到估计值。所以测量所得到的值与估计值哪一个更接近真实值呢?
已知:硬币直径真实值为50mm;
首次估计误差为40mm;
过程误差方差为4e-4;
尺子的误差方差为3。
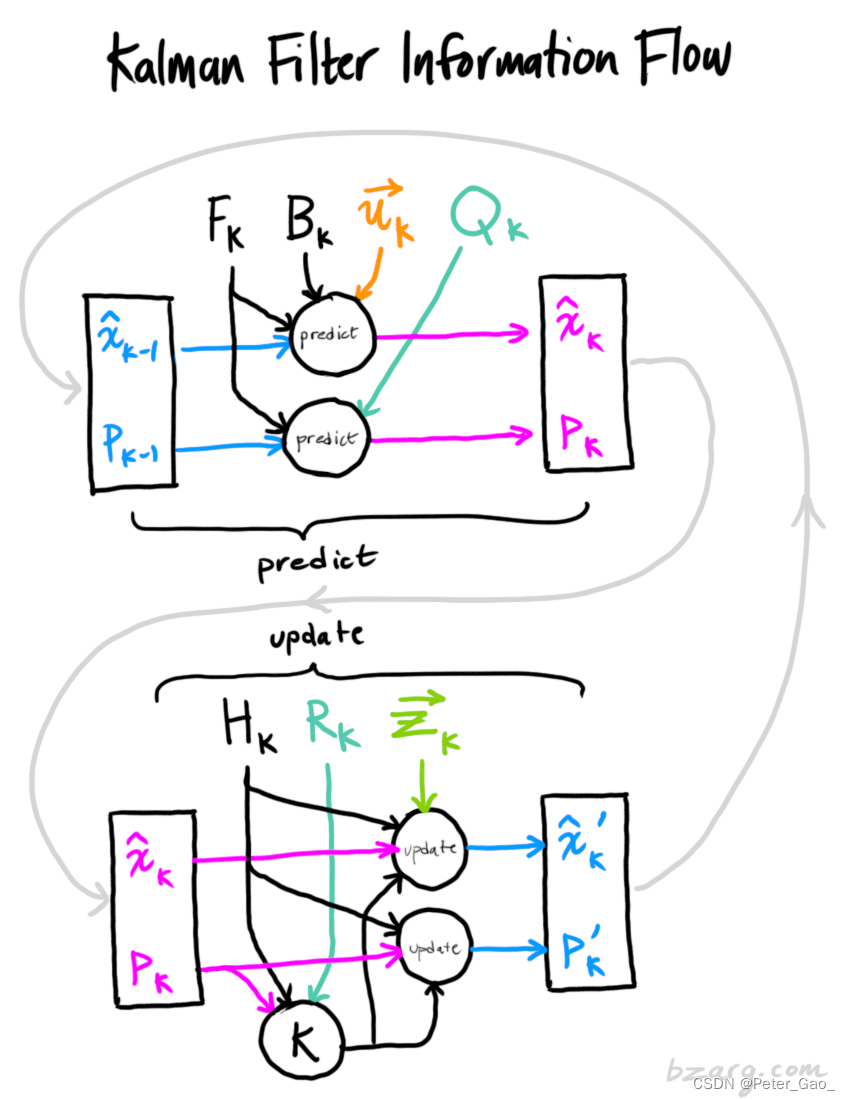
二、流程图
由前面几篇博客对卡尔曼滤波公式进行了仔细的推导,一共得到了五大公式。卡尔曼滤波的过程就是对系统进行预测加矫正的过程,两者循环迭代使系统逐渐趋近于真实值。下面就是卡尔曼滤波过程的流程图。

三、执行过程
一、由k-1次估计的硬币直径 x ^ k − 1 \hat{x}_{k-1} x^k−1 去估计第k次系统的状态值(直径) x ^ k − , x ^ k − = A x ^ k − 1 + B u k − 1 \hat{x}_{k}^{-}, \hat{x}_{k}^{-}=A \hat{x}_{k-1}+B u_{k-1} x^k−,x^k−=Ax^k−1+Buk−1, 对应于本例中系统无输入 u k − 1 = 0 u_{k-1} = 0 uk−1=0 ; A = H = I ; Q = 4 e − 4 ; R = 3 A = H= I;Q = 4e-4;R = 3 A=H=I;Q=4e−4;R=3。则 x ^ k − = x ^ k − 1 = 40 m m \hat{x}_{k}^{-}=\hat{x}_{k-1}=40mm x^k−=x^k−1=40mm。
二、由上一次的误差协方差 P k − 1 P_{k-1} Pk−1 和过程噪声Q预测新的误差 P k − , P k − = P_{k}^{-}, P_{k}^{-}= Pk−,Pk−= A P k − 1 A T + Q A P_{k-1} A^{T}+Q APk−1AT+Q, 对应于本例中 P k − = 5 P_{k}^{-}=5 Pk−=5 。
三、计算卡尔曼增益, K k = P k − H T ( H P k − H T + R ) − 1 K_{k}=P_{k}^{-} H^{T}\left(H P_{k}^{-} H^{T}+R\right)^{-1} Kk=Pk−HT(HPk−HT+R)−1, 对应于本例中 K k = K_{k}= Kk= 5 / ( 5 + 3 ) , K k = 0.625 5/\left(5+3\right), \quad K_{k}=0.625 5/(5+3),Kk=0.625 。
四、 进行校正更新, x ^ k = x ^ k − + K k ( z k − H x ^ k − ) \hat{x}_{k}=\hat{x}_{k}^{-}+K_{k}\left(z_{k}-H \hat{x}_{k}^{-}\right) x^k=x^k−+Kk(zk−Hx^k−), 对应于上例中 x ^ k = 40 + 0.625 ∗ \hat{x}_{k}=40+0.625 * x^k=40+0.625∗ ( z k − 40 ) (z_{k}-40) (zk−40), 此 x ^ k \hat{x}_{k} x^k 即为 k \mathrm{k} k 时刻的最优直径。
五、为下一步估计 k + 1 \mathrm{k}+1 k+1 时刻的最优温度值的迭代进行更新操作, 级更新 P k P_{k} Pk 值, P k = ( I − K k H ) P k − , P_{k}=\left(I-K_{k} H\right) P_{k}^{-}, \quad Pk=(I−KkH)Pk−, 对应于上例中的 ( 1 − K k ) ∗ 5 = 1.875 \left(1-K_{k}\right) * 5=1.875 (1−Kk)∗5=1.875。
| 方法 | kalman 公式 | 对应本例kalman 公式 |
|---|---|---|
| 先验估计 | x ^ k − = A x ^ k − 1 + B u k − 1 \hat{x}_{k}^-=A \hat{x}_{k-1}+B u_{k-1} x^k−=Ax^k−1+Buk−1 | x ^ k − = x ^ k − 1 \hat{x}_{k}^{-}=\hat{x}_{k-1} x^k−=x^k−1 |
| 先验误差协方差矩阵 | P k − = A P k − 1 A T + Q P_{k}^{-}=A P_{k-1} A^{T}+Q Pk−=APk−1AT+Q | P k − = P_{k}^{-}= Pk−= P k − 1 + Q P_{k-1} +Q Pk−1+Q |
| 卡尔曼增益 | K k = P k − H T H P k − H T + R K_{k}=\frac{P_{k}^{-} H^{T}}{H P_{k}^{-} H^{T}+R} Kk=HPk−HT+RPk−HT | K k = P k − P k − + R K_{k}=\frac{P_{k}^{-} }{P_{k}^{-}+R} Kk=Pk−+RPk− |
| 后验估计 | x ^ k = x ^ k − + K k ( z k − H x ^ k − ) \hat{x}_{k}=\hat{x}_{k}^{-}+K_{k}\left(z_{k}-H \hat{x}_{k}^{-}\right) x^k=x^k−+Kk(zk−Hx^k−) | x ^ k = x ^ k − + K k ( z k − x ^ k − ) \hat{x}_{k}=\hat{x}_{k}^{-}+K_{k}\left(z_{k}- \hat{x}_{k}^{-}\right) x^k=x^k−+Kk(zk−x^k−) |
| 更新误差协方差矩阵 | P k = ( I − K k H ) P k − P_{k}=\left(I-K_{k} H\right) P_{k}^{-} Pk=(I−KkH)Pk− | P k = ( I − K k ) P k − P_{k}=\left(I-K_{k} \right) P_{k}^{-} Pk=(I−Kk)Pk− |
四、程序代码
本次程序运行环境为WIN7+MATLAB R2018a
% Kalman filter example
%% 系统描述:
% 1.硬币直径真实值为50mm;
% 2.开始时,硬币直径的估计为40mm,估计误差为5mm;
% 3.尺子的测量误差为3mm;
%% 变量初始化
close all;% intial parameters
% 计算连续n_iter次数
n_iter = 100;
% size of array. n_iter行,1列
sz = [n_iter, 1];
% 硬币直径的真实值
x = 50;
% 过程方差,反应连续两个次直径方差。更改查看效果
Q = 4e-4;
% 测量方差,反应尺子的测量精度。更改查看效果
R = 3;
% z是尺子的测量结果,在真实值的基础上加上了方差为3的高斯噪声。
z = x + sqrt(R)*randn(sz);
%% 对数组进行初始化
% 对直径的后验估计。即在k次,结合尺子当前测量值与k-1次先验估计,得到的最终估计值
xhat = zeros(sz);
% 后验估计的方差
P = zeros(sz);
% 直径的先验估计。即在k-1次,对k时刻直径做出的估计
xhatminus = zeros(sz);
% 先验估计的方差
Pminus = zeros(sz);
% 卡尔曼增益,反应了尺子测量结果与过程模型(即当前时刻与下一次直径相同这一模型)的可信程度
K = zeros(sz);
% intial guesses
xhat(1) = 40; %直径初始估计值为40mm
P(1) =10; % 误差方差为10
%% kalman 方程
for k = 2:n_iter% 时间更新(预测) % 用上一次的最优估计值来作为对本次的直径的预测xhatminus(k) = xhat(k-1);% 预测的方差为上一次直径最优估计值的方差与过程方差之和Pminus(k) = P(k-1)+Q;% 测量更新(校正)% 计算卡尔曼增益K(k) = Pminus(k)/( Pminus(k)+R );% 结合当前时刻尺子的测量值,对上一次的预测进行校正,得到校正后的最优估计。该估计具有最小均方差xhat(k) = xhatminus(k)+K(k)*(z(k)-xhatminus(k));% 计算最终估计值的方差P(k) = (1-K(k))*Pminus(k);
end
%% 作图
FontSize = 14;
LineWidth = 3; % 线宽
figure();
plot(z,'r-*'); %画出尺子的测量值
hold on;
plot(xhat,'b-','LineWidth',LineWidth) %画出最优估计值
hold on;
plot(x*ones(sz),'g-','LineWidth',LineWidth); %画出真实值
grid on;legend('尺子的测量结果', '后验估计', '真实值');
title('kalman 滤波','fontsize',FontSize);
xl = xlabel('次数');
yl = ylabel('直径(mm)');
set(xl,'fontsize',FontSize);
set(yl,'fontsize',FontSize);
hold off;
set(gca,'FontSize',FontSize);% gca:坐标轴序号figure();
valid_iter = 2:n_iter; % Pminus not valid at step 1
% 画出最优估计值的方差
plot(valid_iter,P(valid_iter),'LineWidth',LineWidth);
grid on;legend('后验估计的误差估计');
title('最优估计值的方差','fontsize',FontSize);
xl = xlabel('次数');
yl = ylabel('次数^2');
set(xl,'fontsize',FontSize);
set(yl,'fontsize',FontSize);
set(gca,'FontSize',FontSize);
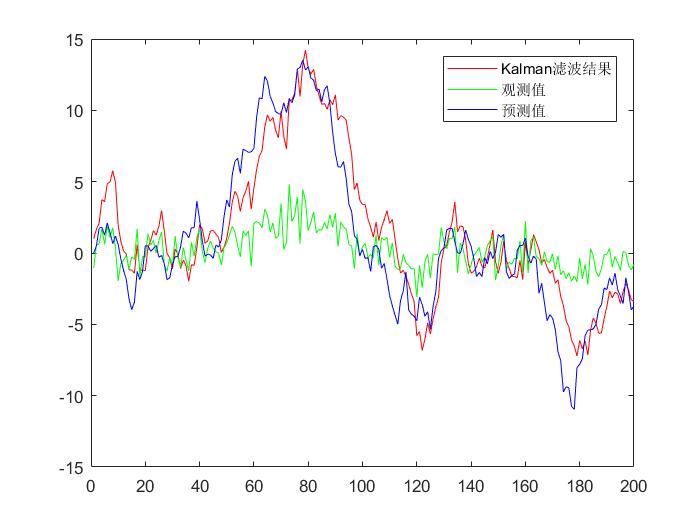
五、仿真结果


参考文献
MATLAB官方文档
二维图绘制官方文档