变量相关概念

变量/常量

所谓变量就是指可以改变的数据量，即数值可以改变。
所谓常量就是指不可以改变的数据量，即数值不可以改变，可以称为“常数”，也可以称为“定数”，与之相反的是变量。
在这里插入图片描述

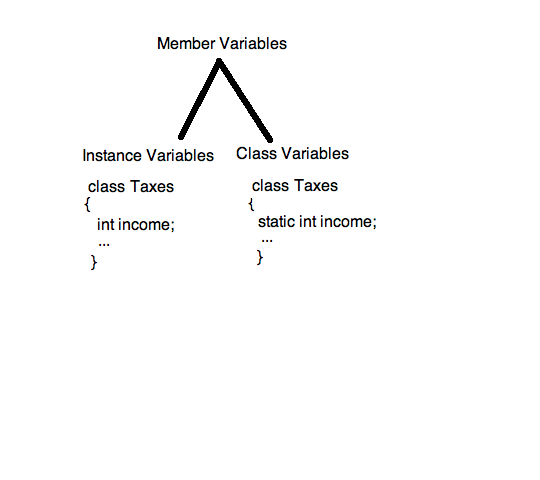
类变量/静态变量

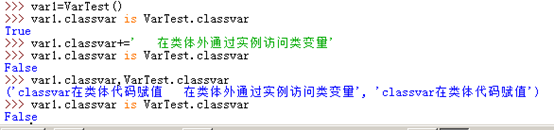
类变量是由 static 修饰的变量，也称为静态变量，可以通过类名访问，也可以通过实例对象来访问，通过对象访问也只是编码阶段这样写而已，在编译的时候会被自动转换成“类名称.变量名”的语法格式。

静态变量也叫字段（field）。

成员变量/实例变量

所谓“成员变量”就是类的成员的变量。类的成员就是类的实例对象，每个实例都有的变量叫成员变量。

非 static 修饰的变量都叫成员变量，也叫实例变量，也可以叫对象变量（很少这样叫），只能通过“实例对象”访问。

成员变量也叫字段（field）。

只有当为成员变量添加 get/set 方法时，我们才称该成员变量是类的属性。

类属性/实例属性/对象属性

类属性就是实例属性，也叫对象属性，是根据 get 方法得来的。

类属性的定义规则：get 方法名，去掉 get 后，将剩余部分首字母小写得到的字符串就是这个类的属性。

例如类 Person 含有方法 getName()，那么 name 就是该类的属性了。

下面例子中，属性名和成员变量名相同，都是 n：

public class Test {private String n; // n是成员变量public String getN() { // n是类的属性return n;}public void setN(String n) {this.n = n;}
}

注：属性名和成员变量名通常情况下相同，这符合 JavaBean 规范。

下面例子中，属性是 name，成员变量 n 不是类的属性：

public class Test {private String n; // n不是类的属性public String getName() { // name是类的属性return n;}public void setName(String n) {this.n = n;}
}

注：上述例子的写法不推荐，不符合 JavaBean 的规范，但是我们要理解。

下面的例子中，我们称 username 为只读属性，因为只能通过 get 方法访问，没有提供写入的方法：

public class Test {private String userName; // userName是成员变量public String getUserName(){ // userName是类的属性return "aaa"; } 
}

什么是 field

类中方法外声明的所有变量（静态变量、成员变量、常量）就是 field，中文译为“字段”或“域”，通常称为“字段”。方法的参数、方法内的局部变量不可以称为 field。

class A {private int a; // private field 私有域protected double b; // protected field 保护域public String c; // public field 公共域A d; // default access field 默认访问域public static Object e; // public static field 公共静态域
}

成员变量和类变量的区别

两个变量的生命周期不同

成员变量随着实例的创建而存在，随着实例对象的回收而消失
静态变量随着类的加载而存在，随着类的消失而消失

访问方式不同

成员变量只能通过对象来访问
静态变量可以通过对象来访问，也可以通过类名来访问，通过对象访问只是在编码阶段，编译期会转换成“类名.变量名”的语法格式

数据存储位置不同

成员变量存储在堆内存的对象中，所以也叫对象的特有数据
静态变量存储在方法区（共享数据区）的静态区，所以也叫对象的共享数据

方法相关概念

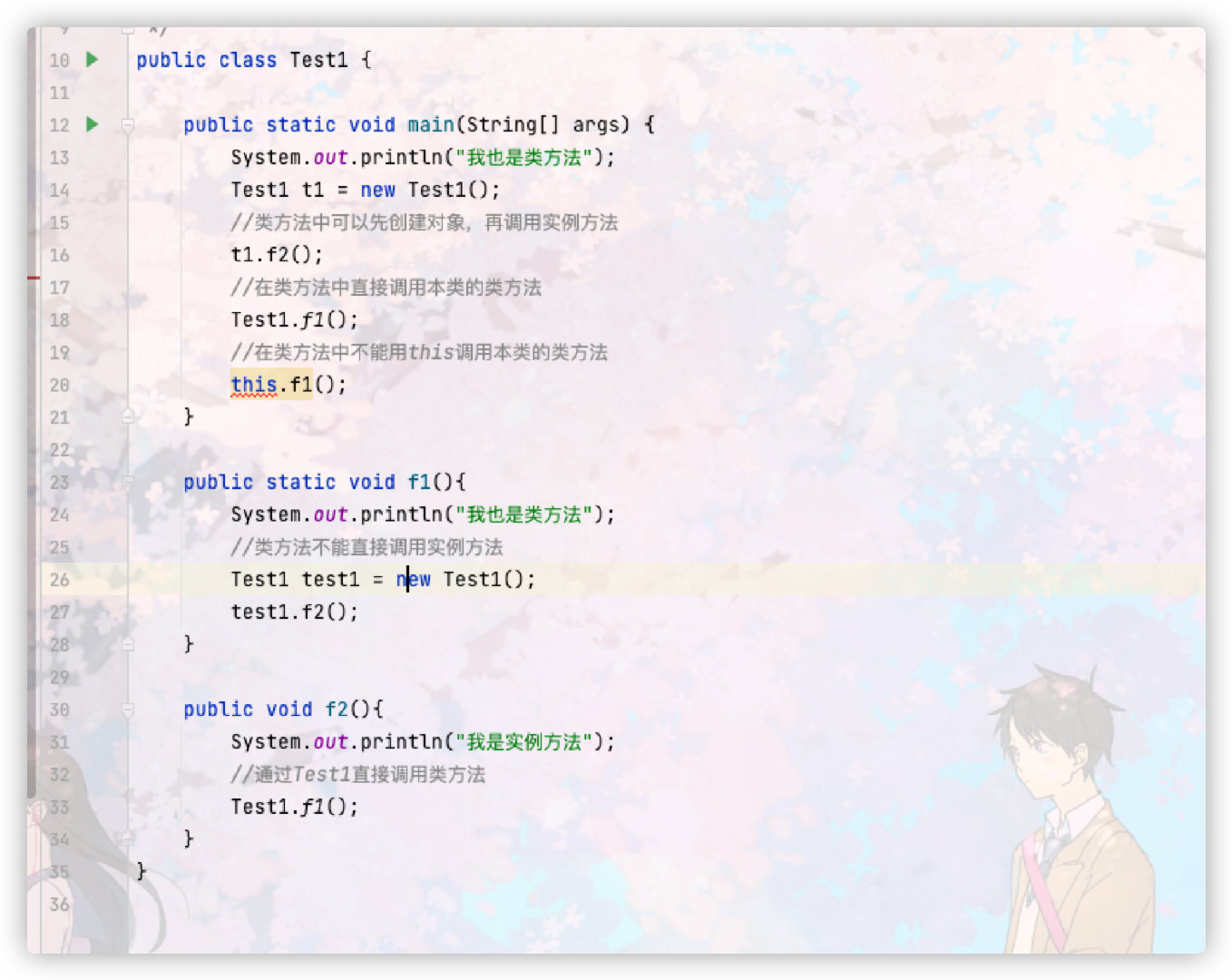
非静态的方法都叫成员方法，必须通过对象才能调用。包含非静态的私有方法、公共方法、保护方法、默认访问权限的方法。私有方法比较特殊，只能通过本类的方法进行调用，但是也必须通过对象才能调用。

静态的方法也叫类方法，只能通过类名进行调用，即便编码时通过对象调用静态方法，编译时也会转换成“类名称.静态方法名”的语法格式。

示例代码

package priv.lwx.javaprac.variable;
public class User {public static final String SKIN_COLOUR = "yellow"; // 这是常量，因为值不变；也叫类变量，也叫静态变量，使用static修饰，仅有一份，所有实例共享，也叫字段（field），不可以称为类属性，因为没有对应的get方法；不可以称为成员变量，因为是通过类名访问，不需要通过对象访问，和对象无关public static String nationality = "china"; // 这叫类变量，也叫静态变量，也叫字段（field），不是成员变量，也不是类属性private String name; // 只能通过对象访问，所以是成员变量，也叫实例变量，也叫字段（field），但是比较特殊，因为是私有的，所以只能由本来的方法才能访问，本类的方法也是通过对象才能访问public String getName() { // name是类的属性，也可以称为实例属性、对象属性，在Java中，类的属性不是看变量，而是看get方法return name;}public void setName(String name) {this.name = name;}
}