turtle科赫雪花的源码分析

article/2025/9/13 1:36:45

python turtle，科赫雪花源码

#KochDrawV1.py
#导入海龟画图的基本库
import turtle
#koch函数是是对科赫函数的基本绘制
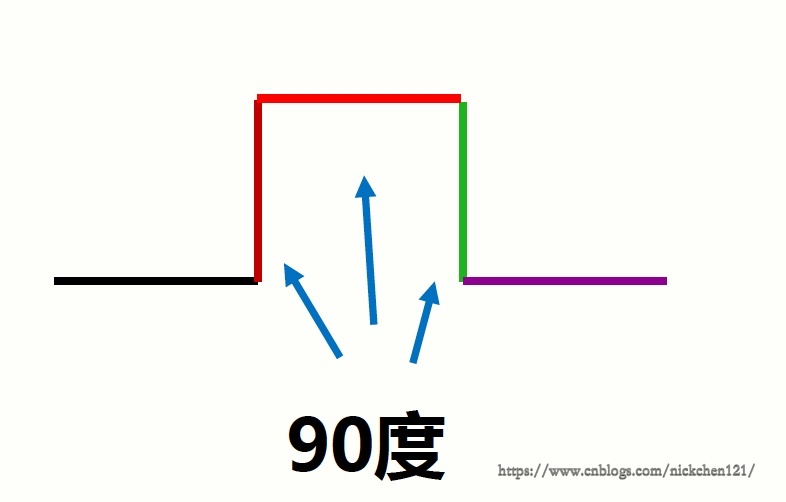
def koch(size,n):if n == 0:turtle.fd(size)else:for angle in [0,60,-120,60]:turtle.left(angle)koch(size/3, n-1)
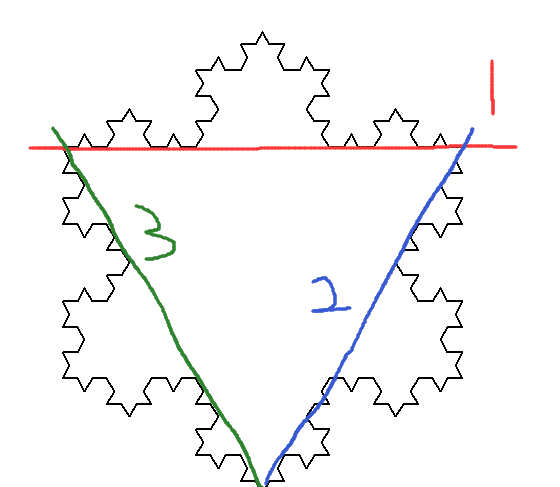
#main函数是对科赫函数的拓展，即koch函数可以看作是绘制三角形的一条边，main函数就是通过调用三次koch画一个完整的三角形
def main():turtle.setup(600,600)#设置窗口大小turtle.penup()#拿起笔turtle.goto(-200,100)#设置距离对应窗口的横坐标X:-200的地方和Y:100的地方turtle.pendown()#放下笔，准备画图turtle.pensize(2)#画笔的尺寸，即粗细koch(400, 3)#调用koch函数画一条科赫图形边turtle.left(-120)#画笔移动方向向逆时针旋转120度koch(400, 3)#调用koch函数画一条科赫图形边turtle.left(-120)#画笔移动方向向逆时针旋转120度koch(400, 3)#调用koch函数画一条科赫图形边turtle.hideturtle()#关闭turtle
main()

重点解析一下koch函数

def koch(size,n):if n = 0:turtle.fd(size)#如果阶数下降到0，以size/（最大阶数）作为长度，angle作为偏移角度来绘制一条直线else:for angle in [0,60,-120,60]:#循环从angle = 0开始, 经过angle = 60，再到angle = -120， 最后到angle = 60结束，一共循环4次turtle.left(angle)#画笔移动方向向顺时针旋转angle度koch(size/3, n-1)#递归执行函数

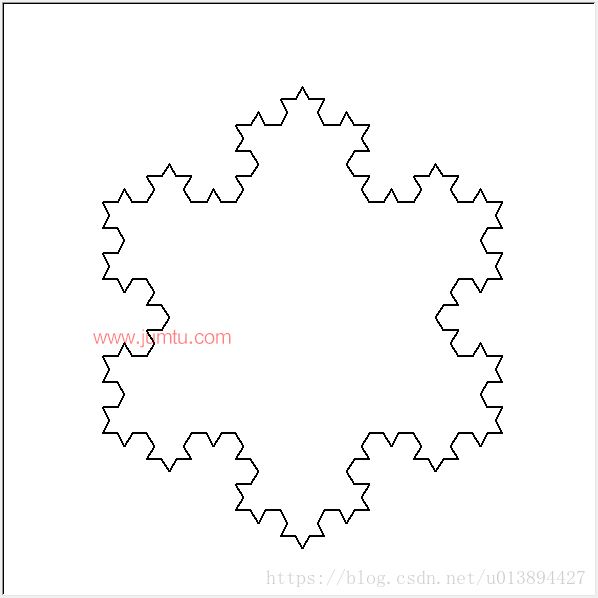
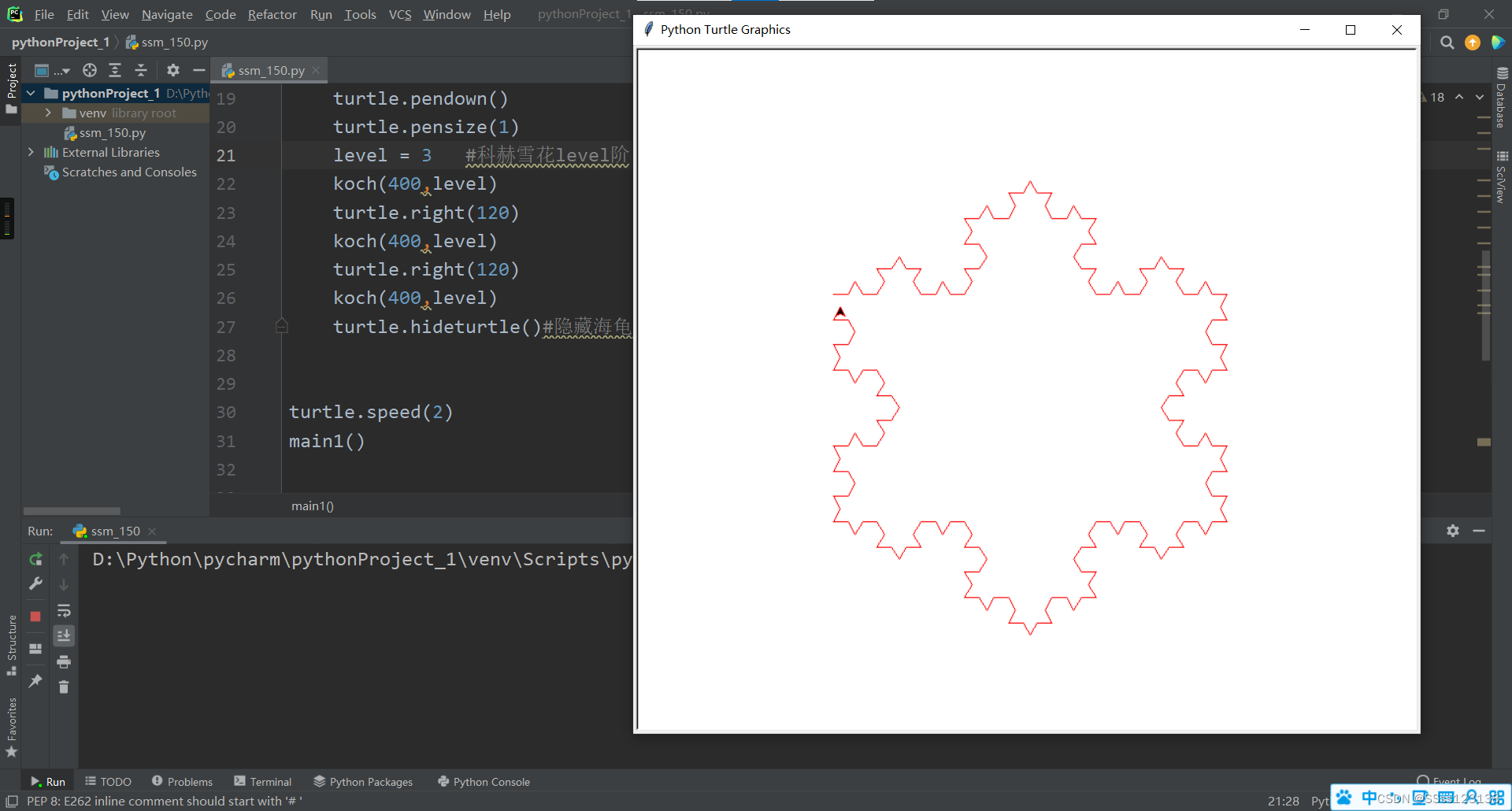
运行结果
在这里插入图片描述

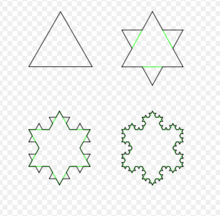
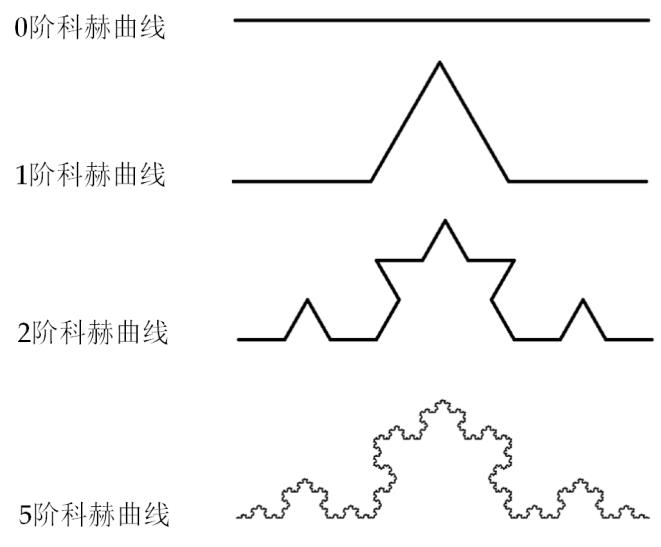
科赫雪花的绘制的关键在于递归函数的使用，这也是递归函数的神奇之处。以科赫雪花程序来分析，这里使用递归来实现，是因为递归函数满足让一个基本的样式实现在细分的时候可以重复调用。

例如，我们写了一个程序实现了把一根长棍子平均分成两段，那么我写的这个程序就是实现这个平分的操作，然后递归就是可以在我平分的这两段棍子中的任一一段再进行这个平分的操作。这就是一个简单的递归过程。